Kondisi Steady State Sistem Bonus Malus Swiss dengan Frekuensi Klaim Binomial Negatif-Lindley
on
Jurnal Matematika Vol. 11, No.2, Desember 2021, pp. 125-134
Article DOI: 10.24843/JMAT.2021.v11.i02.p142
ISSN: 1693-1394
Kondisi Steady State Sistem Bonus Malus Swiss dengan Frekuensi Klaim Binomial Negatif-Lindley
Endang Wahyu H. Universitas Brawijaya ewahyu-math@ub.ac.id
Marji
Universitas Brawijaya marji@ub.ac.id
Abstract: The vehicle insurance premium payment system consists of several states. The division of this state is based on the number of policyholders who submit claims each year. The pattern of changes that occur in the state will result in the search for steady state conditions, namely conditions that have reached stability, do not change the time parameter. The Swiss Bonus-Malus System (BMS) has 22 states with the distribution of the number of claimants being the Lindley-Negative Binomial (r,θ). The method used to obtain a stationary distribution is a recursive method. The results obtained through numerical simulations, for the small value of the parameter r and large, the policyholder tends to state 0 (super bonus).
Keywords: steady state, BMS, negative binomial-Lindley
Abstrak: Sistem pembayaran premi asuransi kendaraan terdiri dari beberapa state. Pembagian state ini didasari oleh banyaknya pemegang polis yang mengajukan klaim setiap tahunnya. Pola perubahan yang terjadi pada state akan mengakibatkan pencarian kondisi steady state yakni kondisi yang sudah mencapai stabil, tidak mengalami perubahan terhadap parameter waktu. Sistem Bonus-Malus Swiss (BMS) memiliki 22 state dengan distribusi dari banyaknya yang mengajukan klaim adalah Binomial Negatif-Lindley (r,θ).Metode yang digunakan untuk mendapatkan distribusi stasioner adalah metode rekursif. Hasil yang diperoleh melalui simulasi numerik, untuk nilai parameter r yang kecil dan θ yang besar maka pemegang polis cenderung ke state 0 yaitu (super bonus).
Kata Kunci: steady state, BMS, Binomial Negatif-Lindley
Salah satu produk asuransi yang banyak diminati oleh masyarakat adalah asuransikendaraan bermotor. Asuransi tersebut bermanfaat untuk memberi kepastian kepada pemegang polis untuk mendapatkan pelayanan biaya perbaikan atau kehilangan
yang ditanggung oleh perusahaan asuransi. Dengan demikian asuransi kendaraan bermotor merupakan solusi dari sifat ketidakpastian dari peristiwa kerusakan atau kehilangan. Ketidakpastian ini menimbulkan kerugian yang berupa risiko.
Risiko terjadinya kerusakan pada kendaraan bermotor akibat kecelakaan atau kehilangan kendaraan mengakibatkan kesadaran masyarakat untuk mengambil polis asuransi kendaraan. Hal tersebut menimbulkan persaingan dari perusahaan asuransi kendaraan. Banyak sistem pembayaran premi dari produk yang ditawarkan perusahaan asuransi yang bertujuan menarik minat masyarakat. Pada umumnya sistem pembayaran premi yang dipakai pada asuransi kendaraan bermotor adalah Sistem Bonus-Malus.
Sistem Bonus Malus dalam asuransi kendaraan bermotor terutama terletak pada besar pembayaran premi, di mana premi yang dibayarkan dipengaruhi oleh frekuensi klaim yang diajukan oleh sipemegang polis. Pada sistem Bonus Malus juga terdapat transisi state dan setiap state memiliki nilai premi yang berbeda. Akibat yang ditimbulkan adalah pemegang polis akan berupaya memperkecil frekuensi klaim. Beberapa negara memiliki sistem Bonus Malus yang berbeda aturan transisi state dan skala premi. Perbedaan setiap negara tergantung dengan kondisi perekonomiannya. Sistem Bonus Malus yang dikenal diantaranya adalah sistem Bonus-Malus Swiss yang terdiri dari 22 state, Brazil 7 state dan Spanyol 5 state. Pada penelitian ini sistem Bonus Malus yang akan dipergunakan sistem Bonus-Malus Swiss.
Penetapan kondisi steady state pada sistem Bonus Malus didasarkan pada pencarian distribusi stasioner yang menyatakan frekuensi klaim setiap tahunnya. Penentuan distribusi stasioner dilakukan dengan menggunakan matriks peluang transisi. Frekuensi pengajuan klaim yang dipergunakan pada penelitian ini merupakan peubah acak yang diasumsikan berdistribusi Binomial Negatif-Lindley. Menurut Roesda (2011) distribusi Binomial Negatif-Lindley sesuai dalam penentuan frekuensi klaim pada asuransi mobil, karena dapat memberikan fitting yang baik. Penelitian tentang distribusi stasioner pada sistem Bonus Malus Swiss telah dilakukan oleh Ballangan dan Sumarno (2002). Pada artikel tersebut, frekuensi pengajuan klaim diasumsikan berdistribusi Poisson dan modifikasi banyak state diasumsikan tak hingga.
Produk akhir setelah memodelkan sistem Bonus Malus Swiss adalah melakukan simulasi data numerik. Hasil yang didapat melalui ilustrasi numerik adalah kondisi steady state yang nantinya dapat mempengaruhi persentase pembayaran premi untuk setiap statenya serta aturan transisi.
Penelitian untuk mendapakan model sistem Bonus Malus Swiss, kondisi steady state serta simulasi data numerik terdiri atas tahapan berikut.
-
1. Identifikasi Masalah
Identifikasi masalah dilakukan dengan melihat jumlah state dan aturan transisi beserta perubahan besar premi pada sistem Bonus-Malus Swiss.
-
2. Studi Literatur
Studi literatur dilakukan dengan mempelajari dan memahami teori yang berhubungan dengan permasalahan.
-
3. Perumusan Masalah
Perumusan masalah dikaitkan dengan identifikasi masalah dan studi literatur untuk mendapatkan kondisi steady state dengan asumsi frekuensi pengajuan klaim berdistribusi Binomial Negatif-Lindley.
-
4. Identifikasi Peubah
Setelah merumuskan masalah, langkah selanjutnya adalah mengidentifikasikan peubah yang diperlukan pada sistem Bonus-Malus Swiss serta untuk mendapatkan kondisi steady state dengan frekuensi pengajuan klaim berdistribusi Binomial Negatif-Lindley. Peubah yang diperlukan adalah:
Besarnya perpindahan state untuk tahun t +1(Y+1), probabilitas transisi state (q(y)) besar kenaikan state setiap terjadi klaim (s) , State dari pemegang polis pada waktu t +1(Xt+1). Fungsi Distribusi Kumulatif untuk Xt+1 (F (x +1)) ,frekuensi pengajuan klaim seorang pemegang polis i pada periode, serta distribusi stasioner f (x). .
-
1. Proses Menentukan kondisi steady state Sistem Bonus-Malus Swiss.
-
a. Menentukan distribusi frekuensi pengajuan klaim yang sukses.
-
b. Menentukan probabilitas transisi state (q(y)) pada skala premi dengan y = —1, s ,2 s ,3 s,...
-
c. Menentukan probabilitas transisi state dengan mencari nilai probabilitas seseorang mengajukan n klaim yang sukses dengan frekuensi pengajuan klaim berdistribusi Binomial Negatif-Lindley. Transisi state dipengaruhi oleh frekuensi klaim yang sukses.
-
d. Menentukan probabilitas dari kondisi steady state
-
5. Simulasi Numerik dan Interpretasi Hasil
Dilakukan perhitungan numerik dari simulasi untuk menghitung probabilitas transisi n langkah yang konvergen dengan bantuan perangkat lunak Matlab dengan input parameter dari distribusi Binomial Negatif-Lindley BN- L(r,θ) . Selanjutnya akan mengamati perubahan perilaku perubahan nilai parameter distribusi BN- L(r,θ) serta melakukan interpretasi dari hasil perhitungan numerik dan analisis data.
-
6. Kesimpulan.
-
3. HASIL DAN PEMBAHASAN
Distribusi frekuensi pengajuan klaim pada penelitian ini menggunakan distribusi Binomial-Negatif-Lindley. Kf merupakan peubah acak yang didefinisikan sebagai frekuensi pengajuan klaim oleh pemegang polis i pada periode ke-1. Kf berdistribusi Binomial Negatif-Lindley dengan dua parameter dua yaitu r dan θ .
Fungsi kepadatan peluang dari BN-L(r,θ) sebagai berikut :
71
P(K f = „)=2_(r + n-hyA (-1) lθ+r+j + l P(K nj « + 1( n )∑(j)( 1) (0 + r+J)2'
J=O
r > 0' 0 > 0.
Pada penelitian ini diasumsikan 0 bernilai konstan.
Pada sistem Bonus-Malus, besarnya premi yang dibayar oleh pemegang polis tiap tahunnya bergantung pada state saat pemegang polis berada. State pemegang polis untuk periode asuransi berikutnya ditentukan secara unik oleh state dan banyaknya klaim yang sukses pada periode saat ini. Jadi masa depan (tingkat untuk tahun t +1) hanya bergantung pada saat ini (tingkat untuk tahun t dan jumlah kecelakaan yang dilaporkan selama tahun t) dan bukan pada masa lalu. Pada sistem Bonus-Malus terdapat state awal ketika pemegang polis membayar premi dasar (Denuit dkk., 2007). Pemegang polis dapat berpindah dari state ke state yang lain. Kondisi steady state dari sistem Bonus Malus dapat tercapai dalam waktu cepat maupun lambat. Apabila keadaan steady state sudah didapat maka probabilitas pemegang polis berada state tersebut akan bernilai tetap untuk
setiap periodenya. Hal ini menunujukkan bahwa distribusi peluang dari state sistem Bonus-Malus sudah stasioner.
Umumnya pencarian distribusi stasioner dilakukan dengan menggunakan matriks peluang transisi. Namun, penggunaan matriks peluang transisi tidak efisien karena terdapat 22 state sehingga menyulitkan dalam penghitungannya. Oleh karena itu, metode yang digunakan di sini adalah metode rekursif.
Pada metode rekursif, jika besarnya perpindahan state untuk tahun t +1 dinotasikan dengan Y , maka
sn
jika tidakadaklaim
jika ada n klaim yang sukses
untuk n = 1,2,3,...; t = 0,1,2,...
-
^i, ^2, ... peubah acak yang diasumsikan saling bebas dan identik dengan fungsi kepadatan peluangnya:
q (y) = PrY = y) y = -1, s ,2 s ,3 s,...
Jika Xt+1 adalah state dari pemegang polis pada waktu t +1, maka Xt+1 didefinisikan
Xt+1 = i
Xt + Yt+1
Xt+1 = 0
21
jika0 ≤ Xt + Yt+1 ≤ 21 jika Xt + Yt+1 =-1 jika Xt + Yt+1 > 21
Fungsi Distribusi Kumulatif untuk X memenuhi hubungan:
FX,+1 (x) = Pr(Xt+1 ≤ x)
21
= Σ fX+1 (x)
x=0
∞
= ∑ Pr(Xt+1 ≤ xYt=1 = y) Pr(Yt+1 = y)
y=-1
∞
= ∑ Pr(Xt+ Yt+1 ≤ χ∖γt+1 = y ^(y)
y=-1
∞
= ∑ Pr( Xt+ y ≤ χ)q(y)
y=-1
∞
= ∑ Pr( Xt ≤ χ - y)q(y)
y=-1
x
= ∑ Fxt (χ - y) q(y) y=-1
Dengan nilai Fx (21) = 1.
Untuk jangka waktu yang tak berhingga Fungsi Distribusi Kumulatif F(x) merupakan limit dari F (x) dan ditulis sebagai:
F (*) = lim fx (*)
x
y=-1
x
= ∑ q (y) lim fx1 (* - y) q (y) t →∞
y=-1
lim Fx (* - y) = lim Pr(Xt ≤ * - y)
21
t→∞ *=0
= lim Pr(Xt = 0 - y) + lim Pr(Xt = 1 - y) + ... + lim Pr(Xt = 21 - y) t →∞ t →∞
Karena lim Pr(Xt = * - y) = πv mengakibatkan t →∞
lim FX ( * - y ) = π 0- y + π1-y + ... + π 21- y
21
= ∑ π* - y
-
*=0
= f (* - y)
Sehingga diperoleh
x
f(*) = ∑ f(* - y)q(y) * = 0,1,2,
y=-1
...,
21
(1)
Persamaan (1) di atas dijabarkan menjadi:
x
F(x) = F(* +1)q(-1) + ∑ F(x - y)q(y) y=0
x
F(* +1) q(-1) = F(*)- ∑ F(* - y) q(y)
F (*+1)=’A;
q(-1)
(2)
V y=0
Persamaan (2) merupakan rumus rekursif, tetapi karena nilai awal F(0) tidak diketahui, maka nilai F(x) tidak dapat langsung dicari. Untuk mencari nilai F(x), dapat
dibangkitkan fungsi-fungsi pembantu A(x) x = 0,1,2,...yang sebanding dengan nilai-
nilai F(x) dengan memilih sembarang A(0) > 0 (Dufresne, 1988), sehingga:
A (x +1)
1
q(-1)
( ^
A( x) -∑ A(x - y) q(y)
1 y=0 √
(3)
Karena F(x) sebanding dengan A(x), sehingga akan dicari nilai A(x) dengan x = 0, 1,
…, 21.
Berikutnya, nilai dari distribusi stasioner didapatkan dengan menggunakan rumus f (x) = F (x) - F (x -1)
Nilai dari distribusi stasioner merupakan nilai fungsi kepadatan peluang.
Dalam melakukan simulasi untuk mencari distribusi stasioner dilakukan secara
numerik. Akan tetapi, terlebih dahulu dihitung perpindahan state q(y) yang bergantung
dengan jumlah banyaknya n klaim yang sukses. Distribusi yang digunakan untuk menghitung probabilitas frekuensi pengajuan klaim adalah distribusi Binomial Negatif-Lindley (r,θ) dengan ekspektasi
E(Ki )=
r -------------7
^ (θ + 1)(θ -1)2
Pemegang polis tidak mengajukan klaim (n = 0) dengan banyaknya klaim sejumlah α, maka besarnya perpindahan state (y) adalah -1.
q (-1) = Pr(K' = 0)
untuk nilai y = 0,1,2,4,5,7,8,10,11,13,14,16,17,19,20 tidak terjadi keterkaitan nilai dengan n, sehingga nilai q (y) = 0
q (0) = q (1) = q (2) = 0
Pemegang polis mengajukan 1 klaim yang sukses (n = 1) dengan banyaknya klaim sejumlah α+1, maka besarnya perpindahan state y adalah 3.
q (3) = Pr(K' = 1)
q (4) = q (5) = 0
q (6) = Pr(K' = 2)
q (7) = q (8) = 0
q (9) = Pr(K' = 3)
q (4) = q (5) = 0
q (6) = Pr(K = 2)
q (7) = q (8) = 0
q (9) = Pr(Ki = 3)
q (10) = q (11) = 0
q (12) = Pr(Ktι = 4)
q (13) = q (14) = 0
q (15) = Pr(Ktt = 5)
q (16) = q (17) = 0
q (18) = Pr(Ktt = 6)
q (19) = q (20) = 0
Dalam menghitung fungsi distribusi kumulatif secara numerik, dilakukan dengan metode rekursif. Langkah untuk menghitungnya sebagai berikut.
-
1. Inisiasi A(0) = 1.
-
2. Menghitung nilai A( x +1) dengan rumus:
A(x +1) = —1
q(-1)
( ^
A(x) -∑ A( x - y) q(y)
x = 0,1,2.
,...,
21
∖
y=0
√
-
3. Menghitung fungsi distribusi kumulatif
f (x) = Ax- x = 0,1,2,
...,
21
A(21)
-
4. Menghitung nilai dari distribusi stasioner
f (x) = F (x) - F (x -1)
Dalam melakukan simulasi numerik untuk menghitung distribusi stasioner secara rekursif digunakan software MATLAB.
Berikut simulasi numerik dengan dengan frekuensi pengajuan klaim berdistribusi BN-L(r, θ) dengan nilai parameter θ konstan dan r yang berubah yaitu BN - L(r = 2, θ = 3), BN- L(r = 4, θ = 3) dan BN-L(r = 6,θ = 3) . Hasil dari simulasi numerik untuk distribusi stasioner ditunjukkan pada Tabel 1 dan Gambar 1.
Tabel 1. Distribusi Stasioner BN - L( r = 2, θ = 3), BN - L( r = 4, θ = 3) dan
BN-L( r = 6,θ = 3)
|
x |
BN-L( r = 2,θ = 3) E (K‘ )= 1.375 |
BN-L( r = 4,θ = 3) E (K ) = 2.75 |
BN-L( r = 6,θ = 3) E (Kt ) = 4.125 |
|
0 |
4.871886×10-6 |
8.921852×10-10 |
2.232848×10-12 |
|
1 |
4.150124×10-6 |
1.536541×10-9 |
5.805405×10-12 |
|
2 |
7.685416×10-6 |
4.182806×10-9 |
2.089945×10-11 |
|
3 |
1.423225×10-5 |
1.138653×10-8 |
7.523805×10-11 |
|
4 |
2.450651×10-5 |
3.050178×10-8 |
2.693967×10-10 |
|
5 |
4.380691×10-5 |
8.218032×10-8 |
9.660314×10-10 |
|
6 |
7.820631×10-5 |
2.213929×10-7 |
3.464044×10-9 |
|
7 |
0.000138548016330527 |
5.960658×10-7 |
1.242035×10-8 |
|
8 |
0.000246521203445138 |
1.605189×10-6 |
4.453450×10-8 |
|
9 |
0.000438509233172364 |
4.322696×10-6 |
1.596830×10-7 |
|
10 |
0.000779333091161371 |
1.164052×10-5 |
5.725592×10-7 |
|
11 |
0.00138580476948001 |
3.134692×10-5 |
2.052967×10-6 |
|
12 |
0.00246409830577657 |
8.441445×10-5 |
7.361119×10-6 |
|
13 |
0.00438095389630377 |
0.000227320380541874 |
2.639402×10-6 |
|
14 |
0.00778949796753785 |
0.000612153152312928 |
9.463839×10-5 |
|
15 |
0.0138498967800387 |
0.00164847283051987 |
0.000339335329896961 |
|
16 |
0.0246251009647901 |
0.00443918740549925 |
0.00121672045233946 |
|
17 |
0.0437838022938377 |
0.0119543281599866 |
0.00436267175563317 |
|
18 |
0.0778481597406185 |
0.0321919190359499 |
0.0156427919088790 |
|
19 |
0.138414797516664 |
0.0866899114378187 |
0.0560887805473212 |
|
20 |
0.246103180438552 |
0.233448050819001 |
0.201111880898441 |
|
21 |
0.437574336358124 |
0.628654378845077 |
0.721106578603123 |
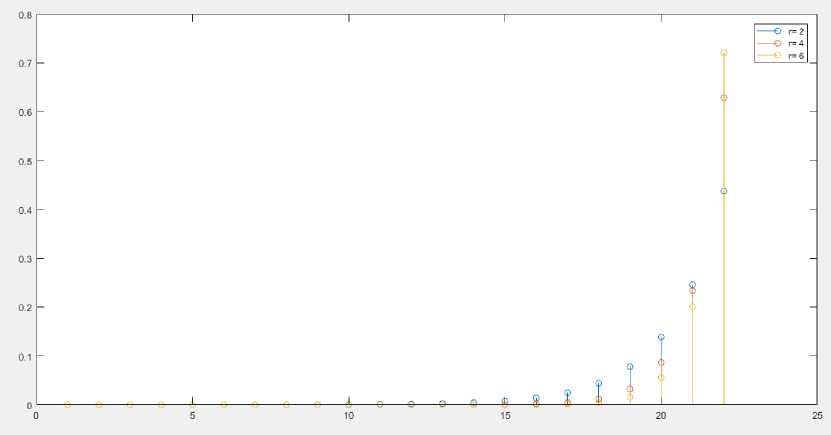
Gambar 1. Grafik Distribusi Stasioner BN - L( r = 2, θ = 3), BN - L( r = 4, θ = 3) dan BN-L( r = 6,θ = 3)
Dari hasil perhitungan pada Tabel 1 yaitu distribusi stasioner BN-L(r,θ) dengan mengambil parameter r berubah dan parameter θ tetap, terlihat bahwa probabilitas pemegang polis berada pada state ke-21 (super malus) semakin besar untuk setiap penambahan nilai n . Sedangkan dengan bertambahnya nilai parameter r, terlihat bahwa kecenderungan pemegang polis berada pada state 0 (state super bonus) semakin besar
untuk nilai n yang semakin kecil. Hal tersebut berarti semakin sedikit frekuensi pengajuan klaim dari pemegang polis.
Berdasarkan tujuan penelitian dan hasil pembahasan maka dapat disimpulkan beberapa hal sebagai berikut.
-
1. Kondisi steady state untuk mencari distribusi stasioner dengan memakai matriks peluang transisi sangat sulit, sehingga digunakan metode rekursif. Distribusi stasioner sistem Bonus-Malus Swiss merupakan suatu fungsi kepadatan peluang. Nilai dari fungsi kepadatan peluang sistem Bonus Malus adalah selisih dari fungsi distribusi komulatif state ke-x dengan state (x-1).
-
2. Hasil simulasi numerik dengan melakukan perubahan terhadap nilai parameter berpengaruh terhadap peluang frekuensi pengajuan klaim. Distribusi stasioner memiliki kecenderungan pada state 0 (super bonus) jika nilai parameter r yang kecil dan θ yang besar.
DAFTAR PUSTAKA
Ballangan, C. G. dan Sumarno, H. 2002. Sebaran Stasioner Pada Sistem Bonus-Malus Swiss serta Modifikasinya. Jurnal Informatika.Vol.3.113-120.
Denuit, M., Xavier, M., Sandra., dan Jean, F. W. 2007. Actuarial Modelling of Claim Counts: Risk Classification, Credibility and Bonus-Malus System. JohnWiley & Sons, Ltd. England.
Dufresne F., (1988). Distributions Stationnaires d’un Systeme Bonus Malus et Probabilite de Ruine. Astin Bulletin. Vol 18. 31-46
Roesda. (2011). Estimasi Parameter distribusi Binomial Negatif-Lindley. Skripsi Sarjana Matematika FMIPA Universitas Brawijaya. Malang.
134
Discussion and feedback