Boosting Neural Network dan Boosting Cart Pada Klasifikasi Diabetes Militus Tipe II
on
Jurnal Matematika Vol. 2 No. 2, Desember 2012. ISSN : 1693-1394
Boosting Neural Network dan Boosting Cart Pada Klasifikasi Diabetes Militus Tipe II
Jerhi Wahyu Fernanda
Jurusan Statistika, Fakultas MIPA, Institut Teknologi Sepuluh Nopember (ITS) e-mail: fernanda.jerhi@gmail.com
Bambang W. Otok
Jalan Arief Rahman Hakin, Surabaya 60111 e-mail: bambang wo@statistika.its.ac.id
Abstract: Diabetes Militus Tipe II merupakan salah satu penyakit yang paling banyak diderita masyarakat Indonesia. Untuk mengantisipasi terkena penyakit DM tipe II, diperlukan suatu tindakan untuk mengurangi resiko terkena penyakit ini dengan mengetahui faktor-faktor resiko yang menyebabkan DM tipe II. Beberapa faktor-faktor resiko yang dapat menyebabkan penyakit ini adalah Riwayat Keturunan, Umur, Jenis Kelamin, Obesitas, Pola Makan, Aktifitas Olahraga. Penelitian tentang klasifikasi DM tipe II telah banyak dilakukan dengan menggunakan metode-metode klasifikasi. Seperti Artificial Neural Network (ANN), CART, dan lain-lain. Tingkat akurasi dari suatu metode klasifikasi seperti ANN, CART dapat ditingkatkan untuk memberikan hasil klasifikasi yang lebih baik dengan menggunakan metode boosting. Boosting adalah metode ensemble yang digunakan untuk meningkatkan akurasi dari suatu metode klasifikasi. Salah satu variasi boosting adalah adaboost. Beberapa penelitian juga telah menunjukkan bahwa adaboost mampu meningkatkan akurasi dari suatu metode klasifikasi. Penelitian ini dilakukan untuk mengkaji implementasi boosting pada metode Feedforwarf Neural Network (FFNN) dan CART. Hasil klasifikasi memperlihatkan bahwa tingkat akurasi dari FFNN dan CART setelah dilakukan boosting mengalami kenaikan dibandingkan sebelum dilakukan proses boosting. Berdasarkan nilai AUC didapatkan metode boosting CART pada iterasi 50, 100, 200, dan 500 memiliki tingkat akurasi yang paling tinggi dengan tingkat akurasi sebesar 98.75% dibandingakan dengan FFNN dan boosting FFNN.
Keywords: Diabetes Militus Tipe II, klasifikasi, FFNN, CART, Boosting
-
1. Pendahuluan
Diabetes Militus tipe II adalah salah satu penyakit yang paling banyak terjadi di Indonesia. Menurut WHO, jumlah penderita diabetes Militus tipe II di Indonesia pada tahun 2010 mencapai 21,3 juta orang. Jumlah ini meningkat dibandingkan dengan jumlah penderita diabetes militus pada tahun 2000 yang hanya 8,4 juta orang. Penderita DM tipe II juga memiliki resiko untuk menderita penyakit yang berhubungan dengan lemak seperti penyakit jantung dan pembuluh darah atau terjadinya komplikasi dengan penyakit lain, sehingga diperlukan suatu tindakan untuk mengurangi resiko terkena penyakit ini. Salah satu tindakan yang dapat dilakukan adalah dengan mengetahui
faktor-faktor resiko dari penyakit ini. Faktor-faktor resiko DM tipe II adalah Riwayat Keturunan, Umur, Jenis Kelamin, Obesitas, Pola Makan, dan Aktivitas Olahraga.
Penelitian-penelitian tentang klasifikasi DM tipe II telah banyak dikembangkan. Metode klasifikasi yang digunakan adalah back propagation neural network, learning vector Quantization neural network, fuzzy k-nearest neighbor, decision tree, dan lain-lain. Tingkat akurasi dari suatu metode klasifikasi dapat ditingkatkan dengan tujuan memberikan hasil klasifikasi yang lebih baik. Salah satu cara yang dapat digunakan adalah dengan menggunakan metode ensemble yaitu boosting. Adaboost yang merupakan variasi dari boosting adalah salah satu metode ensemble yang digunakan untuk meningkatkan akurasi dari suatu metode klasifikasi. Adaboost pertama kali dikembangkan oleh Freund dan Schapire pada tahun 1995. Pada tahun 2002, Breimen, et.all mengimpelentasikan adaboost pada multilayer neural network. Hasilnya adaboost mampu meningkatkan akurasi dari metode multilayer neural network. Pada tahun 2009 Tran et. all juga menerapkan metode adaboost pada probabilitstic Neural Network untuk Novel Intrusion Detection dan hasilnya juga memperlihatkan bahwa adaboost mampu meningkatkan tingka takurasi dari probabilistic neural network.
Penelitian ini dilakukan untuk mengkaji tingkat akurasi yang dihasilkan adaboost ketika diimplementasikan pada metode Feedforward Neural Network (FFNN) dan CART. Kasus yang digunakan adalah kasus DM tipe II dengan melibatkan enam faktor re-siko yaitu riwayat keturunan, umur, jenis kelamin, obesitas, pola makan, dan aktifitas olahraga.
-
2. Tinjauan Pustaka
-
2.1. Feedforward Neural Network
-
Feedforward Neural Network (FFNN) atau Multi Layer Perceptron merupakan neural network yang tersusun dari beberapa layer. FFNN memiliki struktur satu input layer, satu atau lebih hidden layer, dan satu output layer. FFNN sukses dalam menyelesaikan beberapa masalah yang sulit dipecahkan. Algoritma yang sering digunakan dalam FFNN untuk menyelesaiakan kasus adalah algoritma backpropagation.
Fungsi aktivasi merupakan fungsi matematis yang berguna untuk membatasi dan menentukan jangkauan output suatu neuron. Fungsi aktivasi untuk Jaringan Saraf Tiruan Backpropagation harus memiliki beberapa karakteristik penting, yaitu kontinyu, dapat dideferensialkan, dan monoton tanpa penurun. Fungsi aktivasi biasanya digunakan untuk mencari nilai asimtot maksimum dan minimum. Fungsi aktivasi yang biasa digunakan untuk jaringan Backpropagation adalah fungsi sigmoid biner dan fungsi sigmoid bipolar. Di mana fungsi sigmoid biner memiliki jangkauan antara 0 dan 1 dengan fungsinya dirumuskan sebagai
y=f(x) = 1 + 1e-αx (1)
Sedangkan fungsi sigmoid bipolar memiliki jangkauan antara -1 dan 1 dengan fungsinya dirumuskan sebagai
-x y=f(x)=1 e (2)
-
1 + e-x
Fungsi sigmoid bipolar sangat dekat dengan fungsi hyperbolic tangent. Keduanya memiliki range antara -1 sampai 1. Fungsi hyperbolic tangent adalah sebagai berikut.
(3)
y= f(x)
ex - e-x ex + e-x
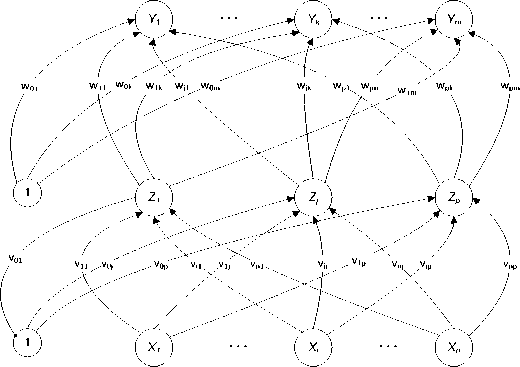
Gambar 1 Struktur backpropagation neural network
Notasi-notasi yang digunakan pada algoritma Backpropagation adalah sebagai berikut
x : vektor input untuk proses pelatihan (training)
x = (x1,··· ,xi,··· ,xn)
t : vektor target output
t = (t1, · · · ,tk, · · · ,tm)
σk : adalah bobot koreksi eror yang telah disesuaikan untuk wjk yang berkaitan dengan eror pada unit keluaran Yk . Simbol ini juga merupakan informasi tentang eror oada unit Yk yang disebarkan kembali pada unit tersembunyi yang berhubungan dengan unit keluaran Yk
σj : adalah bobot koreksi eror yang telah disesuaikan untuk vij yang berkaitan dengan penyebaran kembali informasi eror dari layer ouput ke unit tersembunyi Zj .
α : Learning rate
Xi : unit masukan (input unit) i. Untuk sebuah unit masukan, signal input dan signal output adalah sama dengan nama Xi .
-
v0j : adalah bias pada unit tersembunyi (hidden unit) ke j.
Zj : adalah unit tersembunyi pada j . Unit input ke Zj dinotasikan dengan zinj dengan
n
zinj = v0j + xivij (4)
i
Signal output dari Zj dinotasikan dengan zj = f (zinj ).
-
w0k adalah bias pada output unit ke k , Yk adalah ouput unit ke k . Input ke Yk dino
tasikan yink dengan
yink = w0k + zjwjk (5)
j
Signal output Yk dinotasikan yk dengan yk = f (yink ).
Algoritma yang digunakan untuk pelatihan backpropagation adalah sebagai berikut:
-
1. Inisialisasi bobot (ambil bobot dengan nilai random yang cukup kecil).
-
2. Tetapkan : Maksimum epoh, Target Eror, dan Learning Rate (α)
-
3. Inisialisasi : Epoh = 0
-
4. Ketika kondisi berhenti tidak dapat dipenuhi kerjakan langkah-langkah berikut ini ( Epoh < Maksimum Epoh ) dan ( MSE < Target Eror ) Epoh = Epoh +1.
Langkah Maju (feedforward)
-
a. Untuk setiap unit input (Xi, i = 1, · · · n) meneriman signal input xi dan menyebarkan signal ini ke semua unit pada layar diatasnya (unit tersembunyi).
-
b. Setiap unit tersembunyi (Z,j = 1, · · · , p) menjumlahkan bobot dari signal input dengan persamaan
n
zinj = v0j + xivij (6)
i
dan menerapkan fungsi aktivasi untuk menghitung signal output zj = f (zinj ). dan mengirim signal in ke semua unit pada layer diatasnya ( output unit ).
-
c. Setiap unit output (Yk, k = 1, · · · , m) menjumlahkan bobot dari signal input dengan persamaan
p
yink = w0k + zjwjk (7)
j
dan menerapkan fungsi aktivasi untuk menghitung signal output dengan persamaan yk = f (yink)
Langkah Backpropagation
-
a. Setiap unit output (Yk, k = 1, · · · , m) menerima sebuah pola target berdasarkan pola pada pelatihan input, kemudian menghitung informasi eror dengan persamaan
δk = (tk - yk)f′(yink) (8)
Langkah selanjutnya menghitung bobot koreksi ( untuk mengupdate wjk sebelumnya.
∆wjk = ασkzj (9)
Menghitung koreksi bias dengan menggunakan persamaan ( untuk mengupdate w0 ksebelumnya ) ∆w0k = ασk , dan mengirim σk ke unit pada layer sebelumnya.
-
b. Setiap unit tersembunyi (Zj, j = 1, · · · , p) menjumlahkan input delta (berasal dari layer diatasnya) dengan
m
k=1
Mengalikan dengan fungsi aktivasi untuk menghitung informasi eror dengan perhitungan
Menghitung koreksi bobot ( untuk mengupdate vij sebelumnya )
Dan menghitung koreksi bias (untuk mengupdate v0j sebelumnya)
Update bobot dan bias
-
a. Setiap unit output (Yk, k = 1, · · · , m) update bias dan bobotnya (j = 0, · · · , p) dengan
wjk(baru) = wjk(lama) + ∆wjk(14)
Setiap unit tersembunyi (Zj, j = 1, · · · , p) update bias dan bobotnya (i = 0, · · · , n) dengan
vij (new) = vij (lama) + ∆vij(15)
-
b. Dan test untuk kondisi berhenti
Pemilihan bobot akan akan sangat mempengaruhi ANN dalam mencapai global minimum (atau lokal sa ja) terhadap nilai eror, dan cepat tidaknya proses pelatihan menuju kekonvergenan. Apabila nilai bobot awal terlalu besar , maka input ke lapisan tersembunyi atau lapisan output akan jatuh pada daerah dimana turunan fungsi sigmoidnya akan sangat kecil. Sedangkan jika nilai bobot awal terlalu kecil, maka input ke setiap lapisan tersembunyi atau lapisan output akan sangat kecil. Pemilihan bobot awal dapat dilakukan dengan cara sebagai berikut :
-
a. Inisialisasi bobot secara random
Pemilihan bobot secara random dapat dilakukan dengan inisialisasi secara random dengan nilai antara -0.5 sampati 0.5 ( atau -1 sampai 1, atau interval lainnya )
-
b. Inisialisasi bobot dengan Metode Nguyen-Widrow
Metode ini menginisialisasi bobot-bobot lapisan dengan nilai antara -0.5 sampai 0.5. Sedangkan bobot-bobot dari lapisan input ke lapisan tersembunyi dirancang sedemikian rupa sehingga dapat meningkatkan kemampuan lapisan tersembunyi dalam melakukan proses pembelajaran. Metode ini secara sederhana dapat diterapkan dengan prosedur sebagai berikut:
-
1. Tetapkan : n = jumlah neuron (unit) pada lapisan input
p = Jumlah neuron ( unit ) pada lapisan tersembunyi
β = factor penskalaan (= 0.7(p)1/n).
-
2. Kerjakan untuk setiap unit pada lapisan tersembunyi (j = 1, 2, · · · , p)
-
a. Inisialisai bobot-bobot dari lapisan input ke lapisan tersembunyi
vij = bilangan random antara -0.5 sampai 0.5 (atau antara -g sampai g)
-
b. Hitung ||vij ||
Inisialisasi ulang bobot-bobot:
vij = βij (16)
||vij||
-
2.2. Classification and Regression Tree (CART)
CART merupakan teknik klasifikasi yang sederhana yang banyak digunakan khususnya dalam teknik data mining. Klasifikasi pohon adalah sebuah hasil dari suatu rangkaian perintah dari suatu pertanyaan dan jenis pertanyaan ditanyakan pada setiap langkah pada suatu rangkaian berdasarkan jawaban dari pertanyaan sebelumnya dalam suatu rangkaian. Suatu rangkaian pertanyaan dalam klasifikasi pohon akan berakhir pada prediksi dari suatu kelas ([9]). Langkah-langkah dalam membangun CART
-
a. Splitting Stategy (Strategi pembentukan pohon klasifikasi)
Dalam setiap node, algoritma yang digunakan untuk membangun klasifikasi pohon harus dapat menemukan variabel yang merupakan split (pemilah) terbaik. Dalam pembentukan node ini harus dipertimbangkan untuk menghitung semua variabel yang berfungsi sebagai pemilah dan kemudian menetukan variabel pemilah yang terbaik. Algoritma untuk pembentukan pemilah terbaik ada beberapa teknik. Dalam penelitian ini menggunakan Indeks Gini
(τ) = ∑ p(kτ)p(klτ) = 1 - ∑{p(klτ)}2 (17)
k=k’ k
Dengan p(k |τ) adalah peluang masuk kelas k.
-
b. Pemangkasan pohon klasifikasi (Prunning) Menurut Breiman et al (Izenman, 2008) filosofi dalam membangun klasifikasi pohon adalah dengan membangun suatu pohon klasifikasi yang besar (”large”) dan kemudian melakukan suatu proses pemangkasan dari cabang-cabang klasifikasi sampai didapatkan suatu klasifikasi pohon yang ”right size”. Pemangkasan pohon klasifikasi adalah bagian dari klasifikasi pohon yang berukuran besar. Bagaimana cara memangkas suatu pohon klasifikasi yang berukuran besar terdapat beberapa cara. Disini ditentukan mana yang ”terbaik” dalam memangkas pohon klasifikasi dengan melakukan estimasi terhadap R(T).
Algoritma yang digunakan dalam pemangkasan pohon klasifikasi adalah sebagai berikut.
-
1. Bangunlah suatu klasifikasi pohon dengan ukuran yang besar, dimana kita masih menjaga splitting sampai setiap node terdiri dari kurang dari nmin observasi.
-
2. Hitunglah estimasi dari R(τ ) pada setiap node τ ∈ Tmax
-
3. Pangkaslah Tmax kearah naik keatas pada root nya jadi setiap tingkatan dari proses pemangkasan (pruning) meminimumkan R(T).
Langkah selanjutnya melakukan modifikasi untuk pemangkasan klasifikasi pohon dengan mengadopsi pendekatan yang teratur. Untuk α > 0 menjadi complexity parameter. Untuk setiap node τ ∈ T
Rα(τ) =Rre(τ) +α
Dari persamaan diatas, didefinisikan cost-complexity pruning measure untuk klasifikasi pohon adalah sebagai berikut.
L
Rα(T) = Rα(τl) = Rre(T) + α|T¯| (18)
l=1
Fungsi atau persamaan yang mengoptimalkan proses pemangkasan (optimally pruned subtree) adalah
Rα(T(α)) =Tmin Rα(T) (19)
-
c. Penentuan klasifikasi pohon yang optimum.
Setelah melakukan proses pruning, kendala yang dihadapi adalah kapan proses pruning itu dihentikan dan menghasilkan suatu subtree terbaik dari proses pruning tersebut. Pemilihan subtree terbaik tergantung kepada suatu estimasi yang bagus terhadap R(Tk).
-
2.3. Boosting
Boosting merupakan salah metode ensemble yang digunakan untuk meningkatkan akurasi dari model klasifikasi. Ide dasar dari boosting adalah pada bobot pada proses learning dimana setiap sampel pada proses trainingdiatur memiliki bobot nonnegative (Okun, 2011). Boosting dimulai dengan memberi bobot yang sama pada semua data training (sampel). Setelah memberi bobot pada semua data sampel, proses dilanjutkan dengan menentukan h1 atau dalam boosting dikenal dengan istilah base learner (weak learner) yang merupakan suatu fungsi yang mengklasifikasikan data sampel yang telah diboboti. Base Learner ini bisa didapatkan dari model-model klasifikasi seperti ANN, CART dan lain-lain.

Gambar 2 Alur algoritma ada boost
Diberikan data (x 1 ,y 1), ∙∙∙ , ( xn ,yN) dimana xi ∈ X, yi ∈ Y = {—1, +1}. Inisialisai Wi = 1 /N, i = 1, 2, ∙ ∙ ∙ ,N Untuk m = 1, ∙ ∙ ∙ ,M : Latihlah weak learner Gm dengan menggunakan distribusi widan menghitung error (errm) dan αm dengan persamaan berikut ini
Update
errm =
∑N=ι WiI(yi = Gm(Xi))
∑i=1 Wi
am = M1-=m) 2 errm
wi
wi =
Zt
e-αm jika Gm(xi) = yi [ em jika Gm (Xi) = yi
(20)
(21)
(22)
Dengan Zt adalah factor normalisasi yang dipilih supaya wi berdistribusi. Hipotesa final yang diperoleh adalah
M
G(x) = sign( αmGm (x))
(23)
t =1
-
2.4. Ukuran ketepatan klasifikasi
Kurva Receiver Operating Characteristics (ROC) adalah suatu teknik atau metode yang berfungsi untuk membuat suatu visualisasi, mengorganisasi, dan meyeleksi model klasifikasi terbaik berdasarkan tingkat performansinya.
Dalam ROC terdapat suatu area yang dinamakan Area Under Curve (AUC). AUC sangat berguna untuk membandingkan perfomansi dari beberapa model klasifikasi untuk mengetahui model mana yang terbaik. Perhitungan AUC dapatdilakukan dengan menggunakan persamaan
nD nH
AUC = nD1nH C(di,hj)
(24)
i=1 j=1
Dengan d1, d2, · · · , dnD adalah nilai test untuk distribusi nD setiap subjek, dan h1, h2, ..., hnH adalah nilai test untuk sub jek yang tidak menderita. Nilai dari C(di, hj) adalah
1 jika di > hj
C(di, hj) = 0.5 jika di = hj
(25)
ι0 jika di < h j
-
2.5. Diabetes Militus
Diabetes Melitus (DM) adalah penyakit kronis yang ditandai dengan hiperglikemia, disertai kelainan metabolik sebagai defek sekresi insulin (sel beta pankreas rusak = in-sulitis), atau kerja insulin terganggu, atau keduanya. Hiperglikemia kronis menyebabkan rentetan kerusakan dan disfungsi berbagai jaringan dan berbagai organ : mata, ginjal, saraf, jantung, dan pembuluh darah.
Dari seluruh pengidap DM, lebih dari 90% menderita DM tipe 2. Lain halnya dengan DM tipe 1, perkembangan DM tipe 2 sangat dipengaruhi oleh gaya hidup. Ada dua penyebab utama DM tipe 2. Pertama adalah timbulnya resistensi terhadap insulin. Keadaan ini menyebabkan jaringan tubuh menjadi kurang peka terhadap efek insulin. Akibatnya, glukosa yang beredar dalam darah mengalami kesulitan untuk meninggalkan darah dan memasuki sel-sel tubuh. Untuk menurunkan kadar glukosa darah secara secara efektif dan memenuhi tugas insulin lainnya, dibutuhkan lebih banyak insulin. Penyebab kedua dari DM tipe 2 adalah tidak adanya kemampuan meningkatkan kadar insulin guna memenuhi kebutuhan yang meningkat. Resistensi terhadap insulin, penurunan pelepasan insulin atau keduanya dapat menimbulkan DM tipe 2 (Nathan and Delahanty, 2005).
DM tipe II terjadi ketika gaya hidup diabetogenik(yaitu, asupan kalori berlebihan, pengeluaran kaloritidak memadai,obesitas) yang diletakkan di atas genotipe yang rentan. Indeks massa tubuh di mana berat badan berlebih meningkatkan risiko untuk diabetes bervariasi dengan kelompok-kelompok ras yang berbeda. Sebagai contoh, dibandingkan dengan orang-orang keturunan Eropa, orang-orang dari keturunan Asia tingkat risiko
untuk diabetes pada lebih rendah pada kelebihan berat badan. Hipertensi dan pre-hipertensi yang dihubungkan dengan risiko lebih besar terkena diabetes pada orang kulit putih dibandingkan dengan Amerika dan Afrika.Selain itu, lingkungan di dalam rahim mengakibatkan berat badan lahir rendah dapat mempengaruhi beberapa individu untuk mengembangkan DM tipe II(Khardori, 2011).
Sekitar 90% pasien yang mengidap DM tipe II mengalami obesitas. Pada penelitian prospektif telah menunjukkan bahwa pola makan yang padat energi dapat menjadi faktor risiko perkembangan diabetes yang tidak bergantung pada awal obesitas. Diabetes melitus dapat disebabkan oleh kondisi lain. Beberapa studi menunjukkan bahwa polusi lingkungan mungkin berperan dalam pengembangan dan perkembangan DM tipe II. Sebuah program terstruktur dan terencana diperlukan untuk sepenuhnya mengeksplorasi potensi yang menginduksi diabetes polutan lingkungan.
-
3. Metodologi Penelitian
Data yang digunakan dalam penelitian adalah data sekunder yang terdiri dari 560 pengamatan. Data yang diperoleh terdiri dari variabel dependen atau respon yaitu status pasien apakah menderita DM tipe II atau tidak, dan variabel prediktor dapat dilihat pada Tabel 1.
Tabel 1 Variabel prediktor dalam penelitian
|
Variabel |
Kategori |
Skala Data |
|
Riwayat Keluarga |
Tidak memiliki |
Nominal |
|
Umur |
Rasio | |
|
Jenis Kelamin |
Laki-laki |
Nominal |
|
Perempuan | ||
|
Obesitas |
Tidak mengalami Obesitas |
Nominal |
|
Mengalami Obesitas | ||
|
Pola Makan |
Memenuhi pola makan sehat |
Nominal |
|
Tidak memenuhi pola makan sehat | ||
|
Aktifitas Olahraga |
Tidak aktif/Kurang |
Nominal |
|
Aktif |
Langkah-langkah dalam penelitian secara garis besar dapat dilihat pada Gambar 3 di bawah ini.

Gambar 3 Diagram alur penelitian
-
4. Hasil dan Pembahasan
Analisa data dalam penelitian ini dibagi kedalam empat tahap. Tahap pertama yaitu melihat deskriptif dari variabel prediktor dan variabel respon. Berdasarkan Tabel 2, dapat dilihat bahwa dari 560 pasien, sebanyak 516 pasien menderita DM tipe II dan 44 pasien tidak menderita. Pasien yang memiliki riwayat keturunan DM tipe II ada sebanyak 468 pasien, pasien yang mengalami obesitas ada sebanyak 487 pasien. Deskriptif tentang variabel jenis kelamin, pola makan, dan aktifitas olah raga dilihat pada Tabel 2 di bawah ini.
Tabel 2 Deskripsi Variabel prediktor
|
Variabel |
Kategori |
Frekuensi |
|
Riwayat |
Tidak Ada |
92 |
|
Ada |
468 | |
|
Jenis Kelamin |
Laki-laki |
253 |
|
Perempuan |
307 | |
|
Obesitas |
Tidak |
73 |
|
Ya |
487 | |
|
Pola Makan |
Tidak memenuhi |
102 |
|
Memenuhi |
458 | |
|
Aktifitas Olah |
Raga Kurang |
104 |
|
Aktif |
456 |
Sedangkan untuk umur pasien, rata-rata umur pasien adalah berumur 54 tahun dengan standar deviasi sebesar 10 tahun. Pola sebaran umur pasien dapat diperlihatkan pada histogram pada Gambar 3.

Gambar 4 Histogram Umur pasien
-
4.1. Boosting Feedfoward Neural Network
Sebelum data dianalisis dengan Boosting FFNN, analisis pertama yang dilakukan adalah data dianalisis dengan FFNN. Dalam membangun FFNN, tidak ada ketentuan tentang berapa jumlah neuron yang digunakan. Dalam penelitian ini, untuk membangun FFNN, jumlah neuron yang digunakan adalah 2, 3, 4, dan 5. Dengan jumlah neuron yang berbeda-beda tentunya akan memberikan hasil yang berbeda pula.
Tabel 3 Tingkat akurasi metode FFNN dengan neuron yang berbeda
|
Metode FFNN |
Jumlah Neuron |
Jumlah pengamatan yang misklasifikasi |
Tingkat Akurasi (%) |
|
2 |
22 |
96.1 | |
|
3 |
16 |
97.1 | |
|
4 |
15 |
97.3 | |
|
5 |
15 |
97.3 |
Berdasarkan Tabel 3 diatas dapat dilhat bahwa metode FFNN dengan menggunakan 4 dan 5 neuron memberikan tingkat akurasi yang paling baik. FFNN dengan 4 neuron dipilih sebagai base learner yang akan digunakan dalam proses boosting. Confusion matrix untuk FFNN dengan 4 neuron adalah sebagai berikut.
Tabel 4.Confussion matrix FFNN dengan 4 neuron
|
Model FFNN dengan 4 neuron |
Prediksi | ||
|
Tidak menderita DM tipe II |
Menderita DM tipe II | ||
|
Aktual |
Tidak Menderita DM tipe II |
32 |
12 |
|
Menderita DM tipe II |
3 |
513 | |
Proses boosting pada FFNN dilakukan dengan membangun suatu combine classifier pada pada data awal yang telah diboboti pada variabel responnya. Banyak iterasi yang digunakan dalam proses boosting adalah 50, 100, 200, dan 500. Tingkat akurasi boosting FFNN dapat dilihat pada tabel 5.
Tabel 5 Hasil klasifikasi dengan boosting FFNN
|
Iterasi |
Boosting FFNN |
Prediksi | ||
|
Tidak |
Menderita | |||
|
50 |
Aktual |
Tidak |
35 |
9 |
|
Menderita |
5 |
511 | ||
|
100 |
Aktual |
Tidak |
34 |
10 |
|
Menderita |
4 |
512 | ||
|
200 |
Aktual |
Tidak |
36 |
8 |
|
Menderita |
3 |
513 | ||
|
500 |
Aktual |
Tidak |
39 |
5 |
|
Menderita |
3 |
513 | ||
Berdasarkan Tabel 5 diatas dapat diketahui bahwa dengan melakukan boosting, maka tingkat akurasi dari FFNN akan meningkat. Pada iterasi 500, tingkat akurasinya adalah yang paling tinggi yaitu sebesar 98.57%.Tingkat akurasi ini lebih tinggi daripada tingkat akurasi dari FFNN tanpa boosting.
-
4.2. Boosting CART
Hasil klasifikasi dengan menggunakan CART memiliki dengan tingkat akurasi sebesar
-
97.3%. Tahap selanjutnya dilakukan boosting pada metode CART.
Tabel 6 Hasil klasifikasi dengan metode CART
|
Model CART |
Prediksi | ||
|
Tidak |
Menderita | ||
|
Aktual |
Tidak |
37 |
7 |
|
Menderita |
8 |
508 | |
Tingkat akurasi setelah dilakukan boosting mengalami kenaikan. Pada klasifikasi dengan CART pengamatan yang mis klasifikasi sebanyak 15 pengamatan, setelah dilakukan boosting, jumlah pengamatan yang mis klasifikasi menjadi 7 pengamatan. Hasil klasifikasi pada iterasi 50, 100, 200, dan 500 memiliki tingkat akurasi yang sama.
Tabel 7 Hasil klasifikasi dengan boosting CART
|
Iterasi |
Boosting CART |
Prediksi | ||
|
Tidak |
Menderita | |||
|
50 |
Aktual |
Tidak |
40 |
4 |
|
Menderita |
3 |
513 | ||
|
100 |
Aktual |
Tidak |
40 |
4 |
|
Menderita |
3 |
513 | ||
|
200 |
Aktual |
Tidak |
40 |
4 |
|
Menderita |
3 |
513 | ||
|
500 |
Aktual |
Tidak |
40 |
4 |
|
Menderita |
3 |
513 | ||
-
4.3. Perbandingan Tingkat Akurasi
Perbandingan tingkat akurasi antar metode klasifikasi digunakan untuk mengetahui metode klasifikasi yang paling baik. Tingkat akurasi dari metode-metode klasifikasi yang digunakan terlihat pada tabel di bawah ini.
Tabel 8 Tingkat akurasi tiap metode
|
Metode |
Akurasi (%) |
|
Feedforward Neural Network |
97.3 |
|
Boosting Feedforward Neural Network dengan iterasi 50 |
97.5 |
|
Boosting Feedforward Neural Network Neural Network dengan iterasi 100 |
97.5 |
|
Boosting Feedforward Neural Network Neural Network dengan iterasi 200 |
98.045 |
|
Boosting Feedforward Neural Network Neural Network dengan iterasi 500 |
98.57 |
|
CART |
97.3 |
|
Boosting CART dengan iterasi 50 |
98.75 |
|
Boosting CART dengan iterasi 100 |
98.75 |
|
Boosting CART dengan iterasi 200 |
98.75 |
|
Boosting CART dengan iterasi 500 |
98.75 |
Dari tingkat akurasi metode-metode diatas dapat dibangun suat kurva ROC yang memperlihatkan performansi dari tiap klasifikasi. Berdasarkan kurva ROC, metode yang memiliki sensitivity dan specificity yang paling baik adalah boosting CART dengan iterasi 50, 100, 200, dan 500.
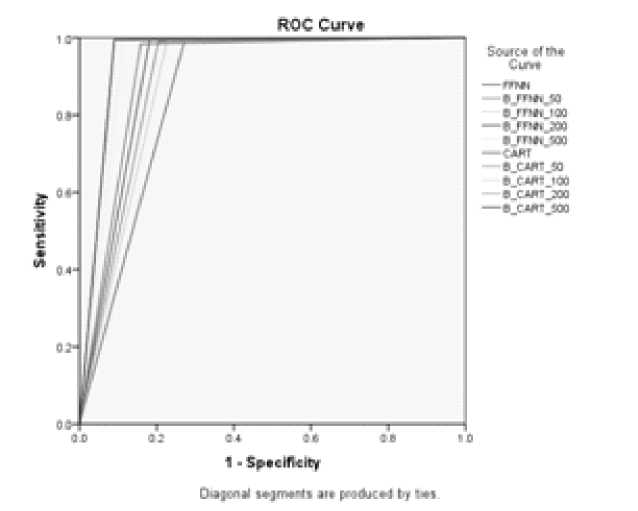
Gambar 5 ROC dari metode klasifikasi
Penentuan klasifikasi terbaik berdasarkan kurva ROC dilakukan denga melihat Area Under Curve (AUC) pada kurva ROC. Boosting CART dengan iterasi 50, 100, 200, dan 500 merupakan metode yang paling baik karenam emiliki nilai AUC yang paling tinggi.
Tabel 8 Nilai AUC tiap metode
|
Area Under the Curve | |
|
Test Result Variable(s) |
Area |
|
FFNN |
.861 |
|
Boosting RBFNN 50 |
.893 |
|
Boosting RNFNN 100 |
.882 |
|
Boosting RBFNN 200 |
.906 |
|
Boosting RBFNN 500 |
.940 |
|
CART |
.913 |
|
Boosting CART 50 |
.952 |
|
Boosting CART 100 |
.952 |
|
Boosting CART 200 |
.952 |
|
Boosting CART 500 |
.952 |
-
5. Kesimpulan
Kesimpulan dari penelitian ini adalah:
-
1. Tingkat akurasi yang dihasilkan dengan metode Feedforward Neural Network memiliki tingkat akurasi sebesar 97.3%. Sedangkan klasifikasi dengan metode CART memiliki tingkat akurasi sebesar 97.3%.
-
2. Implementasi boosting pada model Radial Basis Function Neural Network dan CART mampu meningkatkan tingkat akurasi dari kedua metode tersebut. Untuk implementasi boosting pada FFNN didapatkan tingkat akurasi sebesar yang paling besar yaitu 98.57%. Sedangkan implementasi boosting pada metode klasifikasi CART memiliki tingkat akurasi sebesar 98.75% pada iterasi ke 50, 100, 200, dan 500. Perbandingan antar metode diatas menghasilkan bahwa boosting CART lebih bagus daripada metode boosting FFNN pada kasus dalam penelitian ini.
Daftar Pustaka
-
[1] Adiningsih, R.U. (2011). Faktor-Faktor Yang Berhubungan Dengan Kejadian Diabetes Militus Tipe 2 Pada Orang Dewasadi Kota Padang Panjang. Skripsi S-1 Ilmu Kesehatan Masyaakat Universitas Andalas Padang.
-
[2] Breimen, L., Schwenk, H., Bengio, Y. (2000). Boosting Neural Network. Neural Competition 12, 1869-1807. Massachutes Institute of Technology.
-
[3] Bishop, M.C. (1996). Neural Network for Pattern Recognition. Oxford UK:Clarendon press.
-
[4] Fausset, L. (1994). Fundamental of Neural Network. Architecture, Algorithms, and Application. MIT press.
-
[5] Freund, Y. and Schapire, R.E. (1999). A Short Introduction to Boosting Algorithm. Journal of Japanese Society of Artificial Intelligence 14(5):771-780.
-
[6] Gupta, M.M, Jin, L and Homma N (2003). Static And Dynamic Neural Network From : Fundamentals to Advances Theory. New Jersey Kanada:John Wiley and Sons, Inc.
-
[7] Handayani, S.A. (2003). Faktor-Faktor Risiko Diabetes Melitus Tipe II di Semarang dan Sekitarnya. Thesis S-2 Magister Ilmu Kesehatan Masyarakat Universitas Diponegoro Semarang.
-
[8] Hasti, T., Tibshirani, R, Friedman, J.(2008). The Element of Statistical Learn-ing.Data Mining, Inference and Prediction. New York:Springer Science+Bussines Media, LLC.
-
[9] Izenman, A.J. (2008). Modern Multivariate Statistical Techniques : Regression, Classification and Manifold Learning. New York:Springer Science+Bussines Media, LLC.
-
[10] Jayalakshmi, T., Santhakumaran, A. (2010). Improved Gradient Descent Back Propagation Neural Network for Diagnoses of Type II Diabetes Militus. Global Journal of Computer Science and Technology. Vol.9 Issue 5.
-
[11] Jonathan, S. et. al. (1999). The Epidemiology of Diabetes : a World-Wide Problem. University of Sydney.
-
[12] Kavitha, K., Sarojamma, R.M. (2012). Monitoring of Diabetes with Data Mining via CART Method. International Journal of Emerging Technology and Advanced Engineering, Vol.2, Issue 11.
-
[13] Khardori, R. (2011). Type 2 Diabetes Melitus. http://emedicine.medscape.com/article/117853-overview#a0104. Diakses pada tanggal 25 September 2012 pukul 20.00.
-
[14] Khosasih, E.N, dan Kosasih, A.S. (2008). Tafsiran Hasil Pemeriksaan Laboratorium Klinik. Edisi Kedua, Karisma Publishing Group:Tangerang.
-
[15] Kusumadewi, S., Hartati, S (2006). Neuro-Fuzzy : Integrasi Sistem Fuzzy dan Jaringan Syaraf. Graha Ilmu : Yogyakarta.
-
[16] Lasko, et.al.(2005). The use of receiver operating characteristics curves in biomedical informatics. Journal of Biomedical Informatics 38:404-415.
-
[17] Liang, N., Hegt, H., dan Mladenov, V.M. (2010). Image Ob ject Detections on Boosting Neural Network. 10th Symposium on Neural Network Applications in Electrical Engineering.
-
[18] Mittla, R., et.al. (2011). Measuring obesity:result are poles apart obtained by BMI and bio-electrical impedance analysis. Journal of Biomedical Science and Engineering.
-
[19] Nathan, D.M., Delahanty, L.M. (2009). Menaklukkan Diabetes. Gramedia:Jakarta.
-
[20] Nurkhozin, A., Irawan, M.I., Mukhlash, I. (2011). Klasifikasi Penyakit Diabetes Mellitus Menggunakan Jaringan Syaraf Tiruan BackPropagation dan Lerning Vector Quantization. Prosiding Seminat Nasional Penelitian, Pendidikan dan Penerapan MIPA Fakultas MIPA, Universitas Negeri Yogyakarta.
-
[21] Okun, O., Valentini, G., Re, M. (2011). Ensembles in Machine Learning Applications. New York:Springer Science+Bussines Media, LLC.
-
[22] Okun, O.(2011). Feature Selection and Ensemble Methods for Bioinformat-ics:Algorithmic Classification and Implementations. United States of America:IGI Global
-
[23] Pradhan, M., Kohale, K., Naikade, P., et.all. (2012). Design of Classifier for Detection of Diabetes using Neural Network and Fuzzy k-Nearest Neighbor Algorithm. International Journal Of Computational Engineering Research. Vol.2 Issue 5.
Discussion and feedback