Kontrol Optimal Upaya Pengobatan Penyakit Campak Menggunakan Model Endemi SIR

Jurnal Matematika Vol. 9, No.2, Desember 2019, pp. 94-100                ISSN: 1693-1394

Article DOI: 10.24843/JMAT.2019.v09.i02.p115

Kontrol Optimal Upaya Pengobatan Penyakit Campak Menggunakan Model Endemi SIR

Ida Ayu Putu Ari Utari

Program Studi Matematika, Fakultas MIPA, Universitas Udayana e-mail: [email protected]

Abstract: Measles is an acute highly contagious disease caused by Paramyxovirus. Measles is considered as a dangerous disease because it cause complications, brain and other organs damage, lifelong disability, paralysis and even death. In the previous studies, it was known that the spread of measles highly dependent on number of infected individuals so it is necessary to control measles through treatment. In this paper, we study about the application of the optimal control theory on the system of differential equations of the SIR endemic model. Determination of the optimal control is obtained through the application of the Pontryagin minimum principle. The main target in this paper is to find a unique optimal control where the optimal control can be described as an efficiency rate of treatment in individuals infected with measles to decrease the number of infected individuals.

Keywords: Measles, Optimal control, Pontryagin minimum principle, SIR endemic models, System of differential equations.

• 1.    Pendahuluan

Perubahan lingkungan hidup dan perkembangan ilmu pengetahuan serta teknologi dapat mempengaruhi berbagai macam penyakit yang dapat menimbulkan endemi. Salah satu penyakit yang menyebabkan endemi dan membahayakan manusia adalah penyakit campak (Measles). Penyakit campak adalah suatu penyakit akut yang sangat menular yang disebabkan oleh virus campak golongan Paramyxovirus. Penyakit ini ditandai dengan gejala awal demam, batuk, pilek dan konjungtivis yang kemudian diikuti dengan bercak kemerahan pada kulit (rash) (Widoyono,2005). Penyakit campak sangat berbahaya karena dapat menyebabkan komplikasi, kerusakan organ tubuh dan otak, kelumpuhan dan kematian.

Selain perkembangan ilmu pengetahuan di bidang kedokteran yang memiliki peranan penting dalam pencegahan penyakit campak, bidang matematika juga memberikan peranan penting dalam pencegahan penyebaran penyakit campak (Castellini et al,2009). Peranan tersebut berupa model matematika yang mempelajari penyebaran penyakit dan dapat mencegah penyebaran penyakit endemi seperti campak. Menurut (Widiowati,dkk,2007), pemodelan matematika merupakan bidang matematika yang

merepresentasikan dan menjelaskan sistem fisik atau problem pada dunia nyata kedalam pernyataan matematika, sehingga diperoleh pemahaman dari dunia nyata menjadi tepat.

Kejadian penularan wabah penyakit campak yang terjadi pada suatu populasi dapat dimodelkan ke dalam model matematika salah satunya adalah model SIR (Susceptible, Infected,Recovered). Pada penelitian (Kurniawan,dkk,2012) telah dibahas analisis kestabilan penyebaran penyakit campak (measles) menggunakan model endemi SIR untuk mencari titik kesetimbangan model yaitu titik kesetimbangan bebas penyakit dan titik kesetimbangan endemi. Model endemi SIR menjelaskan pengobatan penyakit campak dapat direpresentasikan sebagai sistem persamaan diferensial biasa nonlinear dengan tiga variabel tak bebas yang meliputi Susceptible (S), Infected (I) dan Recovered (R) (Kurniawan,dkk,2012). Penelitian ini akan mengaplikasikan teori kontrol optimal pada sistem persamaan diferensial dari model matematika SIR yang terbentuk, untuk menentukan bentuk kontrol optimal yang tepat yang dapat digunakan untuk menekan laju pertambahan individu yang terinfeksi penyakit campak.

• 2.    Metode Penelitian

Model matematika SIR diambil dari penelitian (Kurniawan,dkk,2012). Model matematika SIR terdiri dari tiga variabel yaitu Susceptible (S), Infected (I) dan Recovered (R). Model matematika SIR ini dapat digambarkan sebagai berikut :

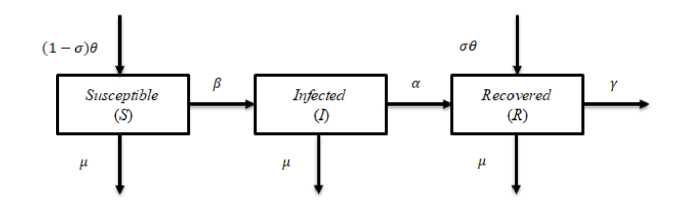
Gambar 1. Model endemi SIR

Didefinisikan,

S : Jumlah individu yang rentan terhadap penyakit campak

I : Jumlah individu yang terinfeksi penyakit campak

R:Jumlah individu yang terinfeksi penyakit campak namun telah sembuh karena pengobatan

β : rate kelahiran rentan.

σ : rate vaksin antara individu rentan dengan individu sembuh

β : rate kontak antara individu rentan dengan individu terinfeksi

a : rate pengobatan

γ : rate migrasi

• I¹ : rate kematian

Hubungan S, I dan R dapat dibentuk dalam persamaan diferensial sebagai berikut :

= (1 - σ)0 - ^S(t)∕(t) - μS(t)

^ = ^wω-^ω-μ⅛)               (1)

= σθ + al(t) - γR(t) - μR(t)

denganS+I+R=l

Langkah-langkah menentukan sistem kontrol optimal pengobatan penyakit campak sebagai berikut :

• 1.    Memodifikasi persamaan (1) dengan melibatkan variabel kontrol optimal yang dinyatakan dengan Ii £ t) .

• 2.    Menentukan fungsi tujuan.

• 3.    Untuk mendapatkan kontrol optimal maka dibentuk fungsi Hamilton yaitu H (S (t),I (t), R (t), u(t), Λ₁, A₂, A₃)

• 4.    Menurut prinsip Pontryagin, fungsi Hamilton mencapai solusi optimal jika persamaan state, costate dan kondisi stasioner terpenuhi (Dewi,2014).

• 3.    Hasil dan Pembahasan

Pada penelitian ini akan diaplikasikan teori kontrol optimal pada sistem persamaan

diferensial dari model matematika SIR yang terbentuk dari persamaan (1). Kontrol optimal yang

tepat dapat digunakan untuk menekan laju pertambahan jumlah individu yang telah terinfeksi

penyakit campak.

Laju pengobatan (treatment) dimodifikasi dengan melibatkan variabel kontrol optimal yang dinyatakan dengan ^u(0 . Secara matematis, model deterministik penyakit

campak yang mengandung variabel kontrol dapat ditulis sebagai berikut :

= (1 - σ)θ - βS(t)l(t} - μS(f)

^ = βS(t)I{t) - α∕(t)(l - w(t)) - μl(t)               (2)

^~ = σθ + al(t) (1 - u(t)) - γR(t) - μR(t)

Koefisien 1 - «(t) usaha pengontrolan terhadap kemungkinan timbulnya penderita penyakit campak yang baru (Sulfayanti,dkk,2011). Kontrol “(O menunjukkan

tingkat efisiensi dari pengobatan yang diberikan pada penderita campak yang terinfeksi. Jika u(t) = 1 maka pengobatan yang diberikan sangat efektif. Sebaliknya jika u(t) = O maka pengobatan yang diberikan sama sekali tidak efektif. Jadi akan dicari bentuk M (t) yang optimal, dimana 0 ≤ u*(t) < 1 sehingga upaya pengobatan yang dilakukan dapat maksimal (Kasbawati,2011).

Teori kontrol optimal pada model penyakit matematika SIR bertujuan untuk meminimumkan jumlah individu yang terinfeksi campak dan jumlah pengobatan yang diberikan selama terinfeksi penyakit campak dengan fungsi tujuan sebagai berikut :

J(u) = ^(lCt) + ^Cu²(t))dt                                (3)

dengan kendala sistem persamaan (2). Sedangkan koefisien C > O adalah koefisien bobot untuk meminimumkan jumlah individu yang terinfeksi dari pengobatan yang dilakukan. Nilai C merupakan nilai penyeimbang dari kontrol yang dilakukan. Selanjutnya akan ditentukan u* sehingga berlaku :

j(u*) = min{/(w):u ∈ U}                                  (4)

dengan U = {w(t): 0 ≤ u(t) ≤ l,Vt ∈ [0,T]}.

Selanjutnya untuk mendapatkan kontrol optimal maka dibentuk fungsi Hamilton yaitu :

H = H(5(t)√(t),Λ(t),u(t),ΛιM₂^₃)

1

= I^ +-Cu² (t) + λ₁(t)((l - σ)θ-βS(t)I(t) - μS(t))

+¹2(^t)(β⁵(Ψ(^t) - α^(t)(l - "(0) - μl(t))

+λ₃(t)(σθ + α∕(t)(l — u(t)) - γR(t) — μR(t))        (5)

Menurut prinsip Pontryagin, fungsi Hamilton mencapai solusi optimal jika persamaan state dan costate serta kondisi stasioner terpenuhi sebagai berikut :

i. Persamaan State

Persamaan state diperoleh dengan menurunkan fungsi Hamilton H terhadap masing-masing λ sebagai berikut :

^- = ((1 - σ)β - βS(t)l(e) - _p5(t))

τr^ = (βs(t)l(t) - al(t) + al(e) u(t) - μl(t})              (6)

— = (σΘ + al(t) - al(t) u(t) - γR(t) - μR(t)}

ii.

iii.

Persamaan Costate

Pada persamaan costate ini, fungsi Hamilton diturunkan masing-masing terhadap variabel state seperti berikut :

- ⅛ = - (-11 ω(-W) - /<) + A,(t)(MO))

^^^s^(¹ + Λ₁(t)(-^S(t)) + -^2(^f)(Λ⁵(O — a + a u(t) — μ) +

^3G)(^{σ - a u}(0))

(7)

-r = ⅛-^

∂R            '

dengan syarat batas (kodisi tranversal) Λ ₁ (f) — Λ^ (t) — A₃ (t) — 0,

Kondisi Stasioner

Stasioner diperoleh dengan menurunkan Hamilton H terhadap variabel kontrol u (t) sebagai berikut :

∂H

r ^{= 0} OU

Cu(t) + λ₂al(t) — λ₃al(t) = 0

karena0≤u≤l, diperoleh

“(0 =

A₃ al (,t)-λ₃al(. t)

(8)

C

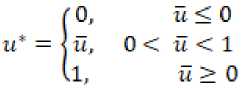
Jadi diperoleh bentuk kontrol optimal u* untuk mengoptimalkan fungsi tujuan yang diberikan sebagai berikut :

u* = min(l, max(0,u)) atau u^t = min (1, max

A₃ al ( r) — A_s a! (t)

C

(9)

Jika kontrol optimal yang diperoleh disubtitusikan ke persamaan state dan costate, maka akan diperoleh persamaan state dan costate yang optimal, sebagai berikut :

iv.

Persamaan state optimal

8H

5 A,

■3

((l-σ)θ-βS(t)I(t)-μS(t))

^βS(t)I(t) — al(t) + «!(t) Jmin ^1, max (θ,

A₃ al (.t)-λ₃al( t)

C

8H

SA₁

θ A₃nJ(t)-A₃crl(t)

• v. Persamaan costate optimal

^ H ⁼ ^ OlWt-Mt) - μ) + Λ_z(t)(∕M(t)))

• /1 + Λι(t)(^-A∙S(t)) + Λ₂(t) {βS(f) — a + a [min(1, max(0,⅛J-⅛i± ))] ^^ y             +⅛(t) (α — α [min ∣ 1, max(θ,½^^-^^^ i i] j             J

~^^~^λ^~^                               (11)

• 4. Kesimpulan dan Saran
  
  Kesimpulan

Pada penelitian ini telah diaplikasikan teori kontrol optimal pada model endemi SIR penyakit campak untuk menentukan bentuk kontrol yang optimal yang dapat menekan laju pertambahan jumlah individu yang terinfeksi. Bentuk kontrol optimal yang diperoleh sebagai berikut :

u* = min(l,max(O,u)) atau u* = min (1, max (θ,^^⅛^^ ))

Dari bentuk persamaan di atas bahwa kontrol optimal yang diperoleh bergantung pada beberapa parameter, diantaranya parameter rata-rata pengobatan penyakit campak, jumlah individu yang terinfeksi penyakit campak serta nilai bobot C . Jika jumlah individu yang terinfeksi campak cukup besar maka diperlukan usaha yang cukup besar untuk mengoptimalkan usaha pengobatan penyakit campak yang dilakukan.

Saran

Pada penelitian ini, ada parameter vaksinasi yang mempengaruhi jumlah individu yang terinfeksi penyakit campak, untuk penelitian kedepannya diharapkan melakukan kontrol optimal untuk pencegahan penyakit campak dengan vaksinasi. Sehingga diperoleh solusi optimal yang lebih baik.

Daftar Pustaka

Castellini,H.&Romanelli,L.2009. On the Propagation of Social Epidemic in So-cial.Networks Under SIR Model. 70:40-53.

Dewi, C. 2014. Kontrol Optimal Model Pertumbuhan Kanker Kandung Kemih dengan Imunoterapi BCG. Universitas Brawijaya.

Kasbawati. 2011. Kontrol Optimal Upaya Pencegahan Infeksi Virus Flu Burung H5N1 dalam Populasi Burung dan Manusia. Jurnal Matematika, Statistika,& Komputasi. Vol. 8,No.1,12-24.

Kurniawan.M.A.& Yuli,F.2012.Analisis Kestabilan Penyebaran Penyakit Campak (Measles) dengan Vaksinasi Menggunakan Model Endemi SIR. Universitas Negeri Yogyakarta.

Sulfayanti, Toaha,S.&Khaeruddin. 2011. Aplikasi Kontrol Optimal pada Perubahan Perilaku Manusia. Jurnal Matematika, Statistika,& Komputasi. Vol. 8,No.1,12-24.

Widiowati&Sutimin. 2007. Bahan Ajar Pemodelan Matematika. Universitas Diponegoro.

Widoyono,S.K. 2005. Penyakit Tropis Epidemiologi, Penularan, Pencegahan & Pemberantasannya. Jakarta:Erlangga.

100