Radikal Prima Bi-Ideal Dalam Semiring Ternari

Jurnal Matematika Vol. 9, No.2, Desember 2019, pp. 78-84

Article DOI: 10.24843/JMAT.2019.v09.i02.p113

ISSN: 1693-1394

Radikal Prima Bi-Ideal Dalam Semiring Ternari

Ratna Sari Widiastuti

Program Studi Matematika, FMIPA, Universitas Udayana e-mail: [email protected]

Abstract: A ternary semiring is an additive commutative semigroup with a ternary multiplication which satisfying some condition. This paper will be discuss about prime biideal radikal in semiring ternary with definition and some theorem. If B is a bi-ideal in semiring ternary T, then radical prime bi-ideal of B in semiring ternary T is an intersection of all prime bi-ideal in semiring ternary T which containing B.

Keywords: bi-ideal, radikal prima, semiring ternary

• 1.    Pendahuluan

Struktur ring apabila digeneralisasi dengan memperlemah grup komutatif atas operasi biner penjumlahan menjadi semigrup komutatif atas operasi biner penjumlahan biasa dan struktur semigrup terhadap perkalian biasa dipertahankan, maka terbentuk struktur baru yang selanjutnya disebut semiring. Hal ini dapat dilihat pada himpunan Z⁺ dengan operasi biner penjumlahan dan perkalian biasa. Sementara itu fenomena semiring ternari dapat dilihat pada himpunan semua bilangan bulat negatif yang disertai operasi penjumlahan biasa dan operasi perkalian biasa. Himpunan semua bilangan bulat negatif jika dikenakan pada operasi perkalian biasa tidak termuat kembali ke dalam himpunan semua bilangan bulat negatif, tetapi termuat dalam himpunan semua bilangan bulat positif. Namun, apabila himpunan semua bilangan bulat negatif dikenakan pada operasi ternary perkalian biasa membentuk struktur semigrup. Selanjutnya, himpunan semua bilangan bulat negatif berlaku sifat distributif kiri, sifat distributif kanan dan sifat distributif tengah penjumlahan terhadap operasi ternary perkalian. Dari sini dapat dimengerti bahwa himpunan semua bilangan bulat negatif merupakan semiring ternari.

Subsemigrup penjumlahan dari semiring ternari yang memenuhi syarat tertentu disebut sebagai ideal dari semiring ternari. Beberapa jenis ideal dalam semiring ternari adalah ideal prima, ideal prima lengkap, ideal semiprima dan ideal semiprima lengkap. Jika A ideal dari semiring ternari T, maka irisan semua ideal prima dari T yang memuat A disebut radikal prima [8]. Selanjutnya, suatu ternari subsemiring pada suatu semiring ternari disebut bi-ideal jika memenuhi syarat tertentu. Himpunan semua bilangan bulat genap negatif merupakan sontoh dari bi-ideal dalam semiring ternari himpunan semua bilangan bulat negatif.

Penelitian ini bertujuan untuk mengetahui bagaimana membangun struktur radikal prima pada bi-ideal. Selain itu diselidiki sifat-sifat yang ada pada radikal prima pada bi-ideal dalam semiring ternari.

• 2.    Dasar Teori

Pertama diberikan definisi mengenai semiring ternari.

Definisi 2.1.[4] Himpunan tak kosong T dengan operasi biner penjumlahan dan ternary perkalian disebut semiring ternari jika T merupakan semigrup komutatif terhadap penjumlahan dan memenuhi:

• (1)    (abcjde = a(bcdje = ab(cdej

• (2)    (a + b)cd = acd + bcd

• (3)    a(b + cjd = abd + acd

• (4)    ab(c + d) = abc + abd

untuk setiap a, b, c, d, e ∈ T.

Himpunan T = {0} dengan operasi biner penjumlahan yang didefinisikan sebagai 0 + 0 = 0 dan ternary perkalian 0 ∙ 0 ∙ 0 = 0 merupakan semiring ternari. Semiring ternari ini disebut semiring ternari null atau semiring ternari zero[5].

Jika A, B, C merupakan himpunan bagian dari semiring ternari T, maka himpunan ABC didefinisikan sebagai berikut:

n

ABC := {∑ a_ib_ic_i ∖a_i ∈ A,b_i ∈ B,c_i ∈ C,n ∈ H)

i=i

dan himpunan A + B didefinisikan sebagai berikut:

A + B = {a + b∖a ∈ A,b ∈ B}.

Definisi 2.2. [4] Semiring ternari T disebut semiring ternari komutatif jika abc = bca = cab = bac = cba = acb untuk setiap a,b,c ∈ T.

Definisi 2.3. [2] Subsemigrup penjumlahan S pada ternary semiring T disebut subsemiring ternari jika s₁s₂s₃ ∈ S untuk setiap s₁, s₂, S₃ ∈ S.

Definisi 2.4. [6] Himpunan bagian tak kosong A dari semiring ternari T disebut ideal kanan (lateral/kiri) dari T jika:

• (1)    Untuk setiap a,b ∈ A berlaku a + b ∈ A.

• (2)    Untuk setiap b,c ∈ T dan untuk setiap a ∈ A berlaku abc (bac/bca) ∈ A.

Definisi 2.5.[6] Himpunan bagian tak kosong A dari semiring ternari T disebut ideal dua sisi dari T jika:

• (1)    Untuk setiap a,b ∈ A berlaku a + b ∈ A.

• (2)    Untuk setiap b,c ∈ T dan untuk setiap a ∈ A berlaku abc, bca ∈ A.

Definisi 2.6. [6] Himpunan bagian tak kosong A dari semiring ternari T disebut ideal dari T jika:

• (1)    Untuk setiap a,b ∈ A berlaku a + b ∈ A.

• (2)    Untuk setiap b,c ∈ T dan untuk setiap a ∈ A berlaku abc, bac, bea ∈ A.

Himpunan A ideal dari semiring ternari T dinotasikan dengan A ≤ T.

Diberikan semiring ternari T dan 0 ≠ S ⊆ T . Didefinisikan S = {A∖A ≤ T,S ⊆ A} .

Dibentuk

(S) = ∩A

.                      A∈S

Teorema 2.7. [8] Himpunan (S) merupakan ideal terkecil dari semiring ternari T yang memuat S.

Definisi 2.8. Diberikan semiring ternari T dan himpunan bagian tak kosong S ⊆ T. Ideal (S) disebut ideal yang dibangun oleh S.

Teorema 2.9. [4] Jika T semiring ternari dan a ∈ T, maka

( n_i             ⁿJ

⁽a⁾ = ∖∑Piqia + ∑

(i=0         j=0

ⁿk

ⁿi

arjSj + ∑ t_kau_k + ∑ v_lw_lax_ly_l + na

k=0

1=0

I

Pi, Qi, rj, Sj, t_k, u_k, v_l, w_l, xι, yι ∈ T, n_i, nj, n_k, n_b n ∈ Z⁺} dengan Σ menyatakan suatu j'umlahan berhingga.

Definisi 2.10. [4] Diberikan semiring ternari T dan a ∈ T. Ideal (a) disebut ideal utama dari semiring ternari T.

Definisi 2.11.[6] Ideal A dari semiring ternari T disebut ideal prima lengkap dari T jika memenuhi x,y,z ∈ T dan xyz ∈ A maka x ∈ A atau y ∈ A atau z ∈ A.

Definisi 2.12. [6] Ideal A dari semiring ternari T disebut ideal prima dari T jika X,Y,Z merupakan ideal dari T dan XYZ ⊆ A, berlaku X ⊆ A atau Y ⊆ A atau Z ⊆ A.

Teorema 2.13. [6] Setiap ideal prima lengkap dari semiring ternari T merupakan ideal prima dari T.

Teorema 2.14. [6] Diberikan T semiring ternari komutatif. Ideal A dari T merupakan ideal prima jika dan hanya jika A merupakan ideal prima lengkap.

Definisi 2.15.[6] Ideal A dari semiring ternari T disebut ideal semiprima lengkap jika x ∈ T sedemikian hingga xⁿ ∈ A, untuk suatu n ∈ N ganjil lebih besar dari satu, maka berlaku x ∈ A.

Teorema 2.16.[6] Setiap ideal prima lengkap dari semiring ternari T merupakan ideal semiprima lengkap dari T.

Jika S merupakan himpunan bagian dari semiring ternari T, maka himpunan Sⁿ, untuk n ∈ M ganjil lebih besar dari satu didefinisikan sebagai berikut:

n

Sⁿ = S.S.∙∙■ . S = {∑x_i.y_i.∙∙∙.z_i ∖x_i,y_i,z_i ∈ S,n ∈ M ganjil lebih besar satu} n faktor     _i=ι  n faktor

Definisi 2.17. [6] Ideal A dari semiring ternari T disebut ideal semiprima jika X ideal dari T sedemikian sehingga Xⁿ ⊆ A, untuk suatu n ∈ M ganjil, berlaku X ⊆ A.

Sifat 2.18. [6] Irisan dari semua ideal semiprima dari semiring ternari merupakan ideal semiprima.

Teorema 2.19. [6] Setiap ideal semiprima lengkap dari semiring ternari T merupakan ideal semiprima dari T.

Teorema 2.20.[6] Diberikan semiring ternari komutatif T. Ideal A dari T merupakan ideal semiprima lengkap j'ika dan hanya j'ika A merupakan ideal semiprima.

Definisi 2.21 [2]Suatu ternari subsemiring B pada semiring ternari S disebut bi-ideal dalam S jika BSBSB ⊆ B.

Proposisi 2.22 [3] Misalkan R , M , dan L merupakan tiga ternari subsemiring dari suatu semiring ternari S dan B = RML . Maka B adalah suatu bi-ideal dari S jika sedikitnya salah satu dari R , M , atau L merupakan ideal kanan, ideal lateral, atau ideal kiri dari S .

Akibat 2.23[3] R adalah ideal kanan, M adalah ideal lateral dan L adalah ideal kiri dari semiring ternari S . Maka suatu ternari subsemiring B dari semiring ternari S merupakan suatu bi-ideal dari S jika B = RML.

Definisi 2.24 [1] Bi-ideal B disebut bi-ideal prima jika X, Y, Z bi-ideal dalam semiring ternari T, XYZ ⊆ B berakibat X⊆ B atau Y ⊆B atau Z ⊆B

Sifat 2.25 Setiap ideal dalam semiring ternari merupakan bi-ideal dalam semiring ternari.

Contoh 2.26

^a={(^{0  0}N^k'¹ ∈ z^-}

A merupakan bi-ideal tetapi bukan ideal dalam semiring ternari Z^-.

• 3.    Hasil dan Pembahasan

Definisi 3.1 Diberikan B bi-ideal dari semiring ternari T. Radikal Prima Bi-ideal dalam semiring ternari T merupakan irisan dari semua bi-idealprima dalam semiring ternari T yang memuat B.

Notasi : √B_b

Diberikan semiring ternari T dan B merupakan bi-ideal dari semiring ternari T. Berikut diberikan notasi-notasi untuk mempermudah pembuktian teorema-teorema selanjutnya.

• B₁    = irisan semua bi-ideal prima dari T yang memuat B.

• B₂    = {x ∈ T∖{x)ⁿ ⊆ B, untuk suatu n ∈ N ganjil}.

Teorema 3.2. Jika B merupakan suatu bi-ideal dari semiring ternari T, maka B ⊆ B₂ ⊆ B₁.

Bukti :

B⊆B2.

Misalkan b ∈ B. Maka {b) ⊆ B dan b ∈ B₂. Diperoleh B ⊆ B₂.

• B2 ⊆ Bi.

Misalkan b ∈ B₂. Maka {b)ⁿ ⊆ B untuk suatu bilangan asli ganjil n. Misalkan P sebarang biideal prima dari T yang memuat B. Maka (b)ⁿ ⊆ B untuk suatu bilangan asli ganjil n, mengakibatkan {b)ⁿ ⊆ P. Karena P bi-ideal prima, {b) ⊆ P dan b ∈ P. Karena benar untuk setiap bi-ideal prima P yang memuat B, b ∈ B₁. Diperoleh B₂ ⊆ B₁.                      ■

Teorema 3.3. Jika A, B, C sebarang tiga bi-ideal dari semiring tenary T, maka

• (i)    A ⊆ B, maka √A_b ⊆ √Bb.

• (ii)    Jika A∩B∩C ≠0, maka √ABC_b = √A∩B∩C_b = √A_b∩√B_b∩√C_b.

(m>√√A_b = √Ab.

Bukti :

• (i)    Misalkan A ⊆ B. Jika P bi-ideal prima yang memuat B, maka P bi-ideal prima yang memuat A. Oleh karena itu, √A_b ⊆ √B_b.

• (ii)    Misalkan P bi-ideal prima yang memuat ABC. Maka ABC ⊆ P dan berlaku A ⊆ P or B ⊆ P or C ⊆ P. Oleh karena itu A ∩ B ∩ C ⊆ P. Jadi, P bi-ideal prima yang memuat A ∩ B ∩ C. Diperoleh bahwa √A ∩ B ∩ Cb ⊆ √ABCb. Misalkan P bi-ideal prima yang memuat A ∩ B ∩ C. Maka A∩B∩C⊆P. Karena ABC ⊆A∩B∩C⊆P, ABC ⊆ P. Sehingga P bi-ideal prima yang memuat ABC. Diperoleh √ABCb ⊆ √A ∩ B ∩ Cb. Jadi, √ABCb = √A ∩ B ∩ Cb. Karena A ∩ B ∩ C ≠ 0, maka A ∩B ∩ C bi-ideal dari T. Misalkan x ∈ √A ∩ B ∩ Cb. Maka terdapat bilangan asli ganjil n sedemikian sehingga xⁿ ∈ A ∩ B ∩ C. Diperoleh xⁿ ∈ A, xⁿ ∈ B, dan xⁿ ∈ C. Sehingga x ∈ √A_b, x ∈ √B_b, dan x ∈ √C_b. Diperoleh x ∈ √Ab ∩ √Bb ∩

√C_b. Sebaliknya, misalkan x ∈ √A_b ∩ √B_b ∩ √C_b, berakibat terdapat bilangan asli ganjil n, m, p sedemikian sehingga xⁿ ∈ A, x^m ∈ B dan x^p ∈ C. Jelas χ^nmP ∈ A ∩ B ∩ C. Sehingga x ∈ √A ∩ B ∩ C_b. Diperolehjika A ∩ B ∩ C ≠ 0, maka √A ∩ B ∩ C_b = √A_b∩√B_b∩√C_b.

(iii) .

Himpunan √A_b irisan dari semua bi-ideal prima dari T memuat A. Kemudian,

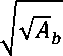
b

merupakan irisan dari semua bi-ideal prima dari T memuat √A_b, berakibat irisan dari semua

bi-ideal prima dari T memuat A adalah √A_b

Diperoleh √√A_b

√^b.

■

Teorema 3.4. Jika B bi-ideal prima dari semiring ternari T, maka √B^b = B, untuk setiap n ∈ ^ ganjil.

Bukti :

Diberikan B merupakan bi-ideal prima dari semiring ternari T. Dengan menggunakan induksi pada n, akan ditunjukkan √B^_b = B. Untuk n = 1 dan karena B bi-ideal prima, maka B ⊆ √B_b ⊆ B, sehingga diperoleh √B_b = B. Lebih lanjut, diasumsikan √B^^_b = B untuk suatu k ∈ ^ ganjil lebih besar satu. Kemudian,

√B^b = √B^kBBb

= √B^kb ∩√Bb∩√B

= B ∩

√Bb∩√Bb

= B

Diperoleh √B^k+2b = B. Dengan induksi terbukti bahwa √B^b = B, untuk setiap n ∈ ^ ganjil.                                                                                          ■

• 4. Kesimpulan dan Saran

Kesimpulan dari penelitian ini adalah radikal prima bi-ideal dalam semiring ternari merupakan irisan dari semua bi-ideal prima dalam semiring ternari yang memuat bi-ideal prima tersebut. Pada penelitian selanjutnya diharapkan dapat mengkontruksi radikal prima dalam biideal minimal dengan menggunakan semua irisan dari bi-ideal minimal dari suatu semiring ternari.

Daftar Pustaka

• [1]    Dheena P. dan Elavarasan B., 2007. Prime Bi-ideals in Ternary Semiring. Journal of the Indian Math. Soc. Vol. 74(3-4), hal: 221-227.

• [2]    Dubey M.K. dan Anuradha. 2012. On Minimal Bi-ideal in Ternary Semirings. International Journal of Algebra, Vol. 6(4), hal: 15-22.

• [3]    Kar S., 2005. On quasi-ideals and bi-ideals in ternari semirings, International Journal Mathematics Sciences, Vol. 18, hal: 3015-3023.

• [4]    Rao, D.M. and Rao, G.S., 2014, A Study on Ternary Semirings, International Journal of Mathematical Archive, 5, pp. 24-30.

• [5]    Rao, D.M. and Rao, G.S., 2015, Prime Radicals and Completely Prime Radicals in Ternary Semirings, International Journal of Basic Sciences and Apllied Computing, 1, pp. 1-5.

• [6]    Rao, D.M. and Rao, G.S., 2015, Structure of Certain Bi-ideals in Ternary Semirings, International Journal of Innovative Science and Modern Engineering (IJISME), 3, pp. 49-56.

• [7]    Widiastuti, Ratna Sari, 2012, Bi-ideal Minimal dalam Semiring Ternary, Skripsi Program Studi S1 Matematika, FMIPA, Universitas Brawijaya.

• [8]    Widiastuti, Ratna Sari, 2016, Radikal Prima dan Radikal Prima Lengkap dalam Semiring Ternary, Tesis Program Studi S2 Matematika, FMIPA, Universitas Gadjah Mada.

84