Jurnal Matematika Vol. 7, No. 2, Desember 2017, pp. 119-123

Article DOI: 10.24843/JMAT.2017.v07.i02.p92

ISSN: 1693-1394

Optimasi Kebutuhan Kendaraan Pengangkut Sampah Menggunakan Model

Fuzzy Goal Programming

Eka Susanti

Jurusan Matematika, Fakultas MIPA, Universitas Sriwijaya

Email: [email protected]

Oki Dwipurwani

Jurusan Matematika, Fakultas MIPA, Universitas Sriwijaya Email: [email protected]

Evi Yuliza

Jurusan Matematika, FMIPA, Universitas Sriwijaya Email: [email protected]

Abstrak: Penelitian ini bertujuan untuk menentukan jumlah optimal kendaraan pengangkut sampah menggunakan model goal programming (GP) dengan pendekatan fuzzy. Jumlah minimum sisa sampah yang tidak terangkut dan muatan kosong kendaraan sebagai goal. Jumlah sampah yang harus diangkut, jumlah ketersediaan kendaraan pengangkut, dan jumlah area layanan dinyatakan dalam bentuk Triangular Fuzzy Number (TFN) dan merupakan kendala pada model fuzzy goal programming (FGP). Model FGP diubah ke bentuk deterministik menggunakan teknik program fuzzy. Dipertimbangkan dua jenis kendaraaan yaitu dumb truck dan armroll. Diberikan contoh perhitungan untuk kecamatan Kalidoni kota Palembang. TFN jumlah sampah adalah (58100, 58150, 58300), TFN jumlah dump truck (190,190,193), TFN jumlah armroll (21,21,22), TFN jumlah minimal wilayah layanan (4,5,5). Diperoleh solusi optimal dengan derajat keanggotaan 0,8 untuk mengangkut sampah sebanyak 58150 kg diperlukan kendaraan jenis dump truck sebanyak 1 kendaraan dan jenis armroll sebanyak 18 kendaraan. Terdapat sisa sampah yang tidak terangkut sebanyak 140 kg.

Kata Kunci: Triangular Fuzzy Number, Model Goal Programming Fuzzy, Teknik Program Fuzzy

  • 1.    Pendahuluan

Penentuan jumlah optimal kendaraan pengangkut sampah merupakan bagian dari analisis sistem pengangkutan. (Eka Susanti, Cahyono, & Dwipurwani, 2016) menganalisis optimalitas kendaraan pengangkut sampah di kecamatan Kertapati menggunakan pemrograman bilangan bulat biner 0 dan 1. Permasalahan pengangkutan sampah dapat dimodelkan dengan model goal programming. Permasalahan goal programming merupakan kasus khusus dari program linier. Dalam goal programming terdapat tiga unsur utama yaitu fungsi tujuan, kendala tujuan, dan kendala non negatif. Koefisien fungsi tujuan, koefisien kendala tujuan nilainya sering tidak diketahui dengan pasti. Untuk mengatasi hal tersebut dapat dilakukan dengan pendekatan fuzzy. (Pal & Kumar, 2013) menggunakan model goal programming dengan pendekatan fuzzy pada masalah optimasi tenaga pembangkit dan distribusi. (Belmokaddem, Mekidiche, & Sahed, 2009) mengaplikasikan model fuzzy goal programming pada perencanaan produksi. Terdapat beberapa bentuk bilangan fuzzy diantaranya bilangan fuzzy segitiga (Triangular Fuzzy Number/TFN). (Gani, Nagoor & Assarudeen, Mohamed, 2012) menerapkan TFN pada penyelesaian program linier. Pada makalah ini diberikan prosedur penyelesaian untuk menyelesaikan model FGP dengan koefisien ruas kanan dinyatakan dengan TFN.

  • 2.    Metode Penyelesaian

Berikut ini diberikan model FGP untuk penentuan jumlah optimal kendaraan pengangkut sampah dengan jumlah minimum sampah dan muatan kosong kendaraan sebagai goal.

Min (DB + DA)

Kendala

n1x1 + n2x2 + DB

-= ()

()

()

()


(3)


  • x1 ≤ S1

χ2 ≤ S2

X1 + X2

,≥0,,.

Keterangan:

: Kendaraan jenis dump truck;   : Kendaraan jenis armroll;   : Kapasitas maksimal

dump truck;    : Kapasitas maksimal armroll;   : TFN jumlah timbulan sampah yang

harus diangkut (a, b, c); ̃ : TFN jumlah ketersediaan dump truck     (d,d,e); ̃ : TFN

jumlah ketersediaan armroll (f,f,g);      : TFN jumlah area layanan (h,i,i);     : sisa

sampah yang tidak terangkut;    : muatan kosong kendaraan

Definisi TFN yang dijelaskan oleh Belman dan zadeh dalam (Susanti & Hartati, 2016) untuk kendala sama dengan (=) diberikan pada gambar berikut ini.


Nilai fungsi keanggotaan untuk TFN pada Gambar 1 adalah

(Xx) =


Definisi T


' 0, x ≤ a atau x ≥ c

X-a          7

—, a ≤ x ≤ b b-c, b~X 7

—, b ≤ x ≤ c.

_ c-b

FN untuk kendala kurang dari atau kurang dari sama dengan (< atau ≤ )


diberikan pada Gambar 2.



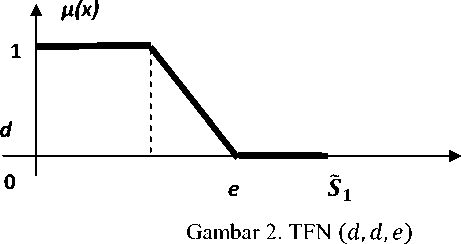
Nilai fungsi keanggotaan untuk TFN pada Gambar 2 adalah

( )=      ,  ≤≤

Berikut diberikan definisi TFN dan nilai fungsi keanggotaan untuk kendala lebih dari atau lebih dari sama dengan (> atau ≥).


Penyelesaian Permasalahan FGP (3) menggunakan teknik program fuzzy. Berikut diberikan prosedur penyelesaian.

DB + DA+(U-L)λ≤U

Ci-(b-a)λ≥a

Ci+(c-b)λ≤ c               C2+(e-d)λ≤e (4) C3   +(9-

f)λ≤g

  • C4 -(i-ℎ)λ≥ℎ

0≤λ≤1,DB, DA≥0,xι , x2 integer

  • 5. Penyelesaian Permasalahan (4) menggunakan software WINQSB

  • 3.    Hasil dan Pembahasan

Sebagai contoh perhitungan diberikan permasalahan penentuan jumlah kendaraan optimal di kecamatan Kalidoni kota Palembang Sumatera Selatan. TFN jumlah sampah adalah (58100, 58150, 58300), TFN jumlah dump truck (190,190,193), TFN jumlah armroll (21,21,22), TFN jumlah minimal wilayah layanan (4,5,5).

Model FGP untuk permasalahan tersebut adalah

Z=Min (DB + DA)

Kendala

4000*1 + 3000*2 + DB - DA = 5̃8150   xι                 ≤ 1̃90 (5)

r∙

¾        ≤21 xI +    X2         ≥5

  • DB, DA≥0,xι , x2 integer.

Langkah penyelesaian Permasalahan (5) adalah sebagai berikut.

  • 1.    Menentukan solusi individu

Z1 =Min (DB + DA )

Kendala

4000xι + 3000X2 + DB - DA = 58100

xι ≤ 190                 (5.a)

  • *2 ≤ 21

xI + X2 ≥4

DB, DA≥0,xι , x2 integer .

Diperoleh solusi xι =1,X2 =18,DB = 100, DA =0,Z1=100

Z2 =Min (DB + DA )

Kendala

4000xι + 3000x2 + DB - DA = 58150

xι ≤ 190                 (5.b)

  • X2 ≤ 21

  • xl + x2 ≥5

  • DB, DA≥0,xι , x2 integer .

Diperoleh solusi xι =1,X2 =18,DB = 150, DA =0,Z1=150

  • Z3 =Min (DB + DA )

Kendala

4000xι + 3000X2 + DB - DA = 58300

xι ≤ 193                 (5.c)

x2 ≤ 22

  • xl + x2 ≥5

  • DB, DA≥0,xι , x2 integer .

Diperoleh solusi xι=1,x2 =18,DB = 300, DA =0,Z1 =300

  • 2.    Nilai maksimum U=300 adalah dan nilai minimum adalahL=100

  • 3.    Bentuk deterministik Permasalahan (5) adalah

Maks λ

Kendala

DB + DA+200λ≤300

4000%1 + 3000x2 + DB - DA-50λ ≥ 58100

4000Xi + 3000x2 + DB - DA+150λ ≤ 58300       (5.c)       Xi +3 λ ≤ 193

x2 +λ ≤ 22

Xi + x2 -A ≥4

0≤A≤1,DB, DA≥0,Xi , x2 integer

Solusi Permasalahan (5.c) adalah Xi=1,X2 =18,DB = 140, DA=0,λ=0,8 . Dengan derajat keanggotaan 0,8, mengambil nilai maksimum solusi individu 300 serta nilai minimum solusi individu 100, untuk mengangkut sampah sebanyak 58150 kg diperlukan kendaraan jenis dump truck sebanyak 1 dan armroll sebanyak 18 kendaraan. Nilai DB =140 berarti bahwa terdapat sisa sampah yang tidak terangkut ke TPA sebanyak 140 kg. Nilai DA=0 berarti pada pengangkutan terakhir tidak terdapat muatan kosong kendaraan. Goal untuk mengangkut semua sampah tidak tercapai, goal untuk memaksimalkan muatan kendaraan tercapai.

  • 4.    Kesimpulan dan Saran

Diperlukan kendaraan jenis dump truck sebanyak 1 kendaraan dan armroll sebanyak 18 kendaraan untuk mengangkut sampah sebanyak 58150 kg. Dengan derajat keanggotaan 0,8, nilai goal fungsi tujuan adalah (200,200,300). Pada permasalahan ini goal untuk minimum sisa sampah tidak tercapai tetapi goal untuk memaksimalkan muatan kendaraan tercapai.

Pada penelitian ini hanya ruas kanan kendala yang dinyatakan dengan bilangan fuzzy. Pada penelitian selanjutnya dapat dilakukan untuk nilai koefisien kendala dan ruas kanan kendala yang dinyatakan dengan bilangan fuzzy.

Daftar Pustaka

Belmokaddem, M., Mekidiche, M., & Sahed, A. (2009). Quantitative Methods Inquires APPLICATION OF A FUZZY GOAL PROGRAMMING APPROACH WITH DIFFERENT IMPORTANCE AND PRIORITIES TO. Journal of Applied Quantitative Methods, 4 No 3(Dm), 317–331.

Gani, Nagoor, A., & Assarudeen, Mohamed, S. . (2012). A new operation on triangular fuzzy number for solving fuzzy linear programming problem A New Operation on Triangular Fuzzy Number for Solving Fuzzy Linear Programming Problem. Applied Mathematical Sciences, , 6 no. 11(September 2014), 525 – 532 A.

Pal, B. B., & Kumar, M. (2013). A linear Fuzzy Goal Programming Method for Solving Optimal Power Generation and Dispatch Problem. International Journal of Advanced Computer Research, Volume-3 N(Issue-8 March-2013), 2249–7277.

Susanti, E., Cahyono, S., & Dwipurwani, O. (2016). Optimasi Kendaraan Pengangkut Sampah di Kecamatan Kertapati Menggunakan Pemrograman Bilangan Bulat Biner 0 dan 1. Jurnal Matematika, 6(2), 79–85.

Susanti, E.,  & Hartati. (2016). Implementasi Bilangan Fuzzy Segitiga Untuk

Menyelesaikan Masalah Goal Programming. In Prosiding SEMIRATA Bidang MIPA 2016; BKS-PTN Barat, Palembang 22-24 Mei 2016 (pp. 677–679).

123