Perbandingan Analisis Metode Peramalan Jumlah Kasus Penyakit Menular di Kota Bandung (Studi Kasus: DInas Kesehatan Kota Bandung)
on
JITTER- Jurnal Ilmiah Teknologi dan Komputer Vol. 3, No. 1 April 2022
Perbandingan Analisis Metode Peramalan Jumlah Kasus Penyakit Menular di Kota Bandung (Studi Kasus: Dinas Kesehatan Kota Bandung)
Marria Tesalonika Siregar1, Gusti Made Arya Sasmita2, Gusti Agung Ayu Putri3
Program Studi Teknologi Informasi, Fakultas Teknik, Universitas Udayana, Bali Bukit Jimbaran, Bali, Indonesia- 803611
e-mail: lonikatesa14@gmail.com, agung.ayuputri@unud.ac.id, aryasasmitha@unud.ac.id.
Abstrak
Kota Bandung merupakan salah satu kota terbesar di Indonesia, sehingga memiliki jumlah penduduk yang cukup padat. Adapun dampak dari kepadatan penduduk dari suatu kota yaitu timbulnya penyebaran jumlah kasus penyakit yang cukup besar. Salah satu cara mencegah penyebaran adalah dengan melakukan prediksi kasus penyakit dengan baik, agar Dinas Kesehatan Kota Bandung mampu meningkatkan layanan kesehatan untuk masyarakat sesuai dengan pertumbuhan data kasus penyakit. Beberapa penyakit menular yang diamati merupakan penyakit yang disebabkan oleh adanya virus, bakteri, maupun parasit dalam tubuh manusia yang dapat menyebar melalui udara, air, maupun penularan langsung dari orang ke orang. Analisis penelitian ini menerapkan metode prediksi dengan membandingkan metode peramalan antara lain regresi linier sederhana, single moving average, dan support vector regression yang kemudian setiap metode diuji tingkat akurasi MAPE dengan hasil yang didapatkan dalam penilitian ini adalah untuk kasus penyakit polio dan tuberkulosis metode terbaik adalah regresi linier sederhana dengan nilai akurasi error adalah 6.91% dan 6.45%, sedangkan kasus penyakit HIV metode terbaik adalah support vector regression dengan nilai akurasi error adalah 36.67%.
Kata kunci: Peramalan, Regresi linier sederhana, Rata-rata bergerak tunggal, Support Vector Regression
Abstract
Bandung is one of largest city in Indonesia, so it has a fairly dense population. As for the impact of the population density of a city, the emergence of the spread of a large number of cases of disease. One way to prevent the spread is to predict disease cases well, so that the Bandung City Health Office is able to improve health services for the community in accordance with the growth of disease case data. Some of the infectious diseases observed are diseases caused by the presence of viruses, bacteria, and parasites in the human body that can be spread through air, water, or direct transmission from person to person. The analysis of this study applies prediction methods by comparing forecasting methods such as simple linear regression, single moving average, and support vector regression which then each method tested mape accuracy rate with the results obtained in this study is for cases of polio and tuberculosis the best method is simple linear regression with error accuracy values of 6.91% and 6.45%, While the best method of HIV disease is support vector regression with an accuracy error value of 36.67%.
Keywords : Forecasting, Simple Linier Regression, Single Moving Average, Support Vector Regression
timbulnya penyebaran jumlah kasus penyakit yang cukup besar. Dinas Kesehatan Kota Bandung merupakan salah satu lembaga pemerintah yang berjalan dalam bidang kesehatan[3]. Salah satu cara mencegah penyebaran adalah dengan melakukan prediksi kasus penyakit dengan baik, agar Dinas Kesehatan Kota Bandung mampu meningkatkan layanan kesehatan untuk masyarakat sesuai dengan pertumbuhan data kasus penyakit.
Beberapa penyakit menular yang diamati merupakan penyakit yang disebabkan oleh adanya virus, bakteri, maupun parasit dalam tubuh manusia yang dapat menyebar melalui udara, air, maupun penularan langsung dari orang ke orang[4].
Analisis penelitian ini menerapkan metode prediksi dengan membandingkan metode peramalan antara lain regresi linier sederhana yaitu metode model probabilistic berfungsi melihat hubungan linier antara dua variabel, dimana salah satu variabel mempengaruhi variabel lainnya. Metode single moving average merupakan salah satu metode peramalan yang menggunakan nilai rata-rata dari n data sebelumnya, dan metode support vector regression yaitu metode regresi yang memiliki tujuan yaitu menentukan sebuah fungsi sebagai suatu hyperlane atau garis pemisah yang membuat error sekecil mungkin dan fungsi regresi yang sesuai dengan semua input data yang kemudian setiap metode diuji tingkat akurasi MAPE.
-
2. Metodologi Penelitian
Penelitian studi kasus ini mengambil data dari Dinas Kesehatan Kota Bandung dengan menggunakan beberapa metode peramalan dalam bahasa pemrogramaan Python. Data penelitian yang digunakan adalah data jumlah kasus penyakit menular dari tahun 2010-2020 dengan banyak data 33 data. Visualisasi data menggunakan library Matplotlib pada Python berbentuk grafik data.
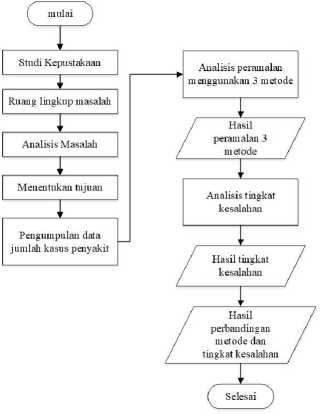
ambar 1. ambaran Umum Penelitian
Gambar 1. merupakan gambaran umum dari penelitian yang akan dilakukan. Langkah pertama dimulai dengan membaca beberapa studi literatur yang akan menjadi referensi, mendefinisikan runag lingkup masalah, analisis masalah, menentukan tujuan penelitian, mengumpulkan data yang diperlukan dalam penelitian, analisis peramalan menggunakan metode yang digunakan yaitu regresi linier sederhana, simple moving average, support vector regression. Setelah mendapatkan hasil peramalan dilakukan pencarian nilai akurasi metode menggunakan MAPE yang kemudian mendapatkan hasil akhir untuk menyimpulkan metode yang layak untuk permalan jumlah kasus penyakit pada tahun berikutnya.
Peramalan yang digunakan memiliki alur perhitungan yang berbeda disetiap metode-metode yang digunakan. Adapun alur perhitungan dari metode regresi linier sederhana adalah sebagai berikut.
Evaluasi metode dengan _ data uji dan data latih
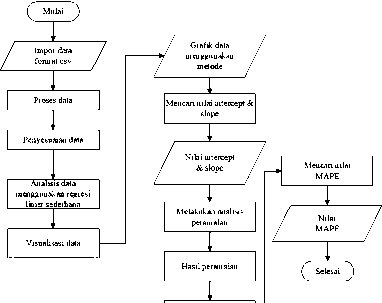
Gambar 2. Alur Perhitungan Regresi Linier Sederhana
Gambar 2 merupakan langkah-langkah alur perhitungan dalam metode regresi linier sederhana yaitu langkah pertama melakukan import data dengan format csv melakukan penyesuaian data dengan membuat matriks, melakukan pemisahan data uji dan data latih kemudian mencari nilai intercept dan slope, kemudian melakukan analisis untuk peramalan pada tahun berikutnya. Langkah terakhir mencari nilai MAPE dan alur perhitungan metode rata-rata bergerak tunggal yang akan dijelaskan sebagai berikut.
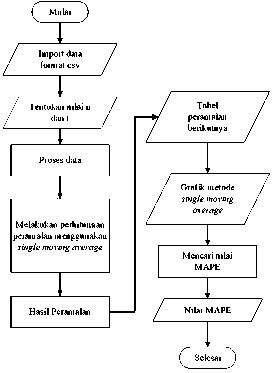
Gambar 3. Alur Perhitungan Simple Moving Average
Gambar 3 merupakan langkah-langkah alur perhitungan data metode simple moving average dengan menentukan nilai n adalah rata-rata data yang digunakan, dan t periode yang akan diprediksi, kemudian memasukan At yaitu data aktual lalu menghitung menggunakan rumus metode dan kemudian mendapatkan hasil peramalan untuk nilai Ft. Terakhir hasil dari nilai peramalan divisualisasikan dengan tabel dan grafik pada Pycharm.
-
3. Kajian Pustaka
Kajian Pustaka merupakan langkah-langkah yang digunakan dalam penelitian peramalan jumlah kasus penyakit dengan menggunakan metode regresi linier sederhana, single moving average, dan support vector regression yang akan dijelaskan sebagai berikut.
-
3.1 Peramalan
Peramalan merupakan suatu cara memperkirakan peristiwa yang akan terjadi dimasa yang akan datang. Metode peramalan ada dua kategori utama yaitu metode kualitatif dan metode kuantitatif. Metode kuantitatif dilakukan apabila terdapat informasi dimasa lalu sedangkan metode kualitatif merupakan metode yang menjadikan pendapat dari para pakar atau ahli sebagai pertimbangan dalam pengambilan keputusan untuk hasil dari peramalan yang telah dilakukan [2].
-
3.2 Regresi Linier Sederhana
Regresi linier sederhana merupakan model probalistik yang berfungsi menyatakan hubungan linier antara dua variabel dimana salah satu variabel mempengaruhi variabel lainnya. Variabel yang mempengaruhi disebut variabel independent sedangkan variabel yang dipengaruhi disebut variabel dependen [6].
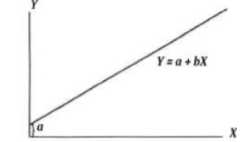
Gambar 4. Contoh Grafik Regresi Linier Sederhana
Persamaan garis linear umum Y = a + bx memiliki dengan keterangan sebagai berikut.
^' = variabel dependen
a = intercept
b = slope
x = variabel independent
Perhitungan intercept dan slope dari persamaan regresi linier sederhana dapat dihitung dengan menggunakan rumus sebagai berikut.
rι. ∑xy — ∑x.∑y
b n. ∑x2 — (∑x)2 (1)
a =
∑y-b.∑x
(2)
Keterangan perhitungan intercept dan slope yaitu n adalah jumlah data, ∑xy adalah jumlah perhitungan nilai x dikali nilai y, ∑x adalah jumlah hasil perhitungan dari nilai x atau nilai independen, ∑y adalah jumlah hasil perhitungan dari nilai y atau nilai dependen, ∑x² adalah jumlah hasil perhitungan akar dari nilai independen, dan b adalah nilai slope.
-
3.3 Simple Moving Average
Rata-rata bergerak tunggal merupakan nilai rata-rata dari n data sebelumnya. Peramalan didasarkan pada proyeksi serial data yang dimuluskan dengan rata-rata bergerak [5]. Satu set data kemudian dihitung rata-ratanya, selanjutnya digunakan untuk sebagai peramalan utnuk periode berikutnya.
e∙ _ V⅛≤‰)
Contoh rumus perhitungan metode single moving average dengan keterangan yaitu sebagai berikut.
Ft + ι = peramalan untuk periode yang ingin dicari
Xt = nilai aktual periode ke t
n = total batas data dalam metode
Metode single moving average memiliki dua sifat khusus yaitu dalam membuat peramalan memerlukan data historis dalam jangka waktu tertentu. Jika mempunyai data selama x periode [5], maka bisa membuat peramalan untuk periode ke Jt + 1 dan sifat kedua yaitu semakin
panjang jangka waktu rata-rata bergerak tunggal maka akan menghasilkan rata-rata bergerak yang baik atau mulus.
-
3.4 Support Vector Regression
Support vector regression merupakan salah satu metode pengembangan yang ada pada support vector machine untuk metode regresi yang memiliki tujuan yaitu menentukan sebuah fungsi sebagai suatu hyperlane atau garis pemisah yang membuat error sekecil mungkin dan fungsi regresi yang sesuai dengan semua input data [1]. Pendekatan metode kernel memiliki beberapa aspek yang salah satunya adalah feature scaling yang bisa digunakan pada kernel linier dan tidak linier.
f M = ∑'=ι(αi- ai∖ ^"(^iλ) + b (4)
Keterangan:
f(χ)= nilai prediksi
XiX =niali yg sudah di feature scaling pada kernel
Cli = data aktual
k = banyak data
-
3.5 Mean Absolute Percentage Error
MAPE merupakan salah satu akurasi peramalan yang menampilkan persentase ukuran error atau kesalahan relatif atau persentase kesalahan hasil peramalan terhadap permintaan aktual selama periode tertentu [2].
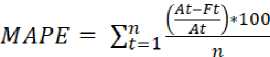
(5)
Keterangan:
At = Nilai aktual pada periode t
Ft = Nilai peramalan pada periode t
n = Jumlah periode peramalan yang terlibat
Tabel 1. Intepretasi Nilai MAPE
|
Nilai MAPE |
Interpretasi |
|
< 10% |
Sangat Bagus |
|
10-20% |
Bagus |
|
20-50% |
Cukup |
|
> 50% |
Tidak Bagus |
Tabel 1. merupakan tabel interpretasi nilai MAPE dengan kategori terdiri dari 4 bagian yaitu sangat bagus, bagus, cukup, dan tidak bagus.
-
4. Hasil dan Pembahasan
Peramalan jumlah kasus penyakit di Kota Bandung dilakukan berdasarkan 3 kategori kasus penyakit. Ketiga kategori penyakit ini masuk kedalam penyakit menular yang diamati oleh Dinas Kesehatan Kota Bandung yaitu polio, tuberkulosis, dan Human Immunodeficiency Viruses.
-
4.1. Regresi Linier Sederhana
Perhitungan peramalan menggunakan metode regresi linier sederhana dengan bahasa pemrogramaan Python dan menggunakan platfrom Pycharm pada kasus penyakit polio.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
Kode Program 1. Import Library pada Python
Kode Program 1. menjelaskan tentang library yang digunakan dalam peramalan menggunakan metode regresi linier sederhana.
jumlah = pd.read_csv
r'C:\Users\user\PycharmProjects\TAtest\newpenyakit.csv') jumlah_df = pd.DataFrame(jumlah, columns = ['Tahun', 'Polio'])
Kode Program 2. Import Data Kasus Penyakit Polio
Kode program 2. menjelaskan tentang import data newpenyakit.csv yang berlokasi di local C dengan variabel jumlah dengan menggunakanl library Pandas untuk membaca data tersebut.
x = np.array(jumlah_df['Tahun'])
y = np.array(jumlah_df['Polio'])
x = x.reshape(-1,1)
Kode Program 3. Penyesuaian Dataset Polio
Kode program 3. menjelaskan tentang penyesuaian dataset dengan menggunakan variabel x dan y. variabel x dan y menggunakan library Numpy dengan memanggil kolom pada jumlah_df yaitu tahun dan polio.
from sklearn.linier_model import LinierRegression
model = LinierRegression() model.fit(x,y)
Kode Program 4. Model Regresi Linier Sederhana pada Python
Kode program 4. menjelaskan tentang memanggil model regresi linier pada library Sklearn. library Sklearn digunakan untuk melakukan analisis dengan salah satunya metode regresi linier.
x_vis = np.array([0,12]).reshape(-1,1)
y_vis = model.predict(x_vis)
plt.scatter(x,y)
plt.plot(x_vis, y_vis, '-r')
plt.xlabel("Tahun")
plt.ylabel("Polio")
plt.title("Grafik Jumlah Kasus Polio")
plt.grid(True)
plt.show()
Kode Program 5. Visualisasi Metode Regresi Linier pada Kasus Penyakit Polio
Kode Program 5. menjelaskan tentang visualisasi dataset setelah dilakukan regresi linier sederharna yaitu variabel x_vis dan y_vis digunakan untuk melakukan visualisasi regresi linier dengan x_vis menggunakan library Numpy dengan range 0 sampai 12 periode tahun dengan reshape -1,1.
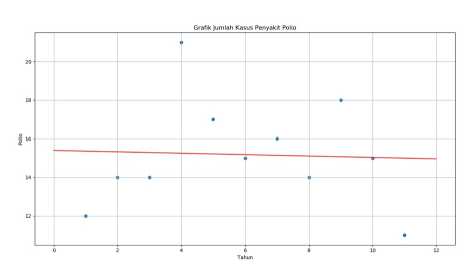
Gambar 5. Visualisasi Peramalan Metode Regresi Linier Sederharna Kasus Penyakit Polio
Gambar 5. menjelaskan tentang hasil grafik visualisasi dataset dengan garis merah sebagai gambaran jumlah kasus selanjutnya.
print(f'intercept: {jml_penyakit}') print(f'slope: {jml_penyakit}')
Kode Program 6. Mencari Nilai Intercept dan Slope
Kode program 6. menjelaskan tentang mencari nilai intercept dan slope denggan menggunakan library Sklearn dengan memanggil jml_penyakit untuk intercept dan jml_penyakit untuk slope.
intercept: 15.4
slope: [-0.03636364]
Gambar 6. Nilai Intercept dan Slope Kasus Penyakit Polio
Gambar 6. menjelaskan hasil intercept yaitu 15.44 dan nilai slope yaitu -0.036, Langkah selanjutnya melakukan peramalan jumlah kasus penyakit polio yang akan dijelaskan sebagai berikut.
jml_penyakit = np.array([12]).reshape(-1,1) prediksi_penyakit = model.predict(jml_penyakit) print(f'Prediksi Jumlah Kasus Penyakit Berikutnya: {prediksi_penyakit}')
Kode Program 7. Analisis Peramalan Jumlah Kasus Penyakit Polio
Kode program 7. menjelaskan tentang prediksi jumlah kasus penyakit selanjutnya dengan variabel jml_penyakit menggunakan library Numpy dengan array 11 yaitu periode yang akan diprediksi dengan hasil yang akan dijelaskan sebagai berikut.
Prediksi Jumlah Kasus Penyakit Berikutnya: [14.96363636]
Gambar 7. Hasil Peramalan Kasus Penyakit Polio
Gambar 7. menjelaskan tentang hasil dari prediksi pada tahun 2021 atau pada tahun berikutnya adalah 14.96 yang digenapkan menjadi 15 kasus penyakit polio.
|
from sklearn.model_selection import |
train_test |
_split |
|
x_train, x_test, y_train, y_test = test_size=0.2,random_state=0) train_test_split(y, shuffle=False) model = LinierRegression() model.fit(x_train,y_train) |
train_test_ |
split(x,y, |
Kode Program 8. Mencari data latih dan data uji
Kode program 8. menjelaskan tentang library Sklearn yang digunakan untuk mencari data uji dan data latih dalam studi kasus. Package yang digunakan adalah train_test_split yang dimana memiliki 4 variabel yaitu x_train, x_test, y_train, dan y_test dengan parameter x, y dan perbandingan data uji dan coba adalah 80:20.
from numpy import mean, abs
y_pred = model.predict(x_test)
mape= mean(abs((y_test - y_pred)/y_test))*100
print('MAPE : %.2f%%' %mape)
Kode Program 9. Menghitung Akurasi MAPE
Kode program 9. menjelaskan tentang menghitung tingkat akurasi peramalan metode regresi linier sederhana yaitu dengan menggunakan mean absolute percentage error. Tingkat akurasi peramalan menggunakan Numpy. Hasil dari semua tingkat akurasi peramalan akan dijelaskan sebagai berikut.
MAPE : 6.91%
Gambar 7. Hasil MAPE Kasus Penyakit Polio
Gambar 7. menjelaskan tentang hasil nilai tingkat akurasi peramalan mean absolute percentage error bernilai 6.91%.
-
4.2. Single Moving Average
Perhitungan peramalan menggunakan metode regresi linier sederhana dengan bahasa pemrogramaan Python dan menggunakan platfrom Pycharm pada kasus penyakit polio.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
Kode Program 10. Import Library pada Python
Kode Program 10. menjelaskan tentang library yang digunakan dalam peramalan menggunakan metode single moving average antara lain, Numpy, Matplotlib dan Pandas.
jumlah=pd.read_csv(r'C:\Users\user\PycharmProjects\TAtest\ newpenyakit.csv')
jumlah_df = pd.DataFrame(jumlah, columns = ['Tahun', 'Polio'])
Kode Program 11. Import data CSV
Kode program 11. menjelaskan tentang import data newpenyakit.csv yang berlokasi di local C dengan variabel jumlah dengan menggunakan library Pandas untuk membaca data tersebut.
jumlah_df['Prediksi_Selanjutnya']=
jumlah_df['Polio'].rolling(window=3).mean()
jumlah_df['Prediksi_Selanjutnya']=
jumlah_df['Prediksi_Selanjutnya'].replace(np.nan,0) print(jumlah_df)
Kode Program 12. Peramalan Metode Single Moving Average
Kode program 12. menjelaskan tentang metode single moving average dengan variabel jumlah_df parameter prediksi selanjutnya sama dengan jumlah_df pada kolom polio pada data dengan menetapkan asumsi n = 3.
|
Tahun |
Polio Prediksi |
_Selanjutnya | |
|
0 |
1 |
12 |
0.000000 |
|
1 |
2 |
14 |
0.000000 |
|
2 |
3 |
14 |
13.333333 |
|
3 |
4 |
21 |
16.333333 |
|
4 |
5 |
17 |
17.333333 |
|
5 |
6 |
15 |
17.666667 |
|
6 |
7 |
16 |
16.000000 |
|
7 |
8 |
14 |
15.000000 |
|
8 |
9 |
18 |
16.000000 |
|
9 |
10 |
15 |
15.666667 |
10 11 11 14.666667
Gambar 8. Hasil Peramalan dengan Metode Single Moving Average
Gambar 8. menjelaskan tentang hasil dari prediksi selanjutnya pada metode single moving average yang ada pada tahun ke-11 atau urutan ke-10 pada peramalan dengan nilai 14.67 yang digenapkan menjadi 15 kasus penyakit polio.
a = range(len(jumlah_df))
plt.scatter (a,jumlah_df['Polio'], color= 'red', label = 'Data Aktual')
plt.plot (a,jumlah_df['Prediksi_Selanjutnya'], label = 'Data
Prediksi')
plt.xlabel("Tahun")
plt.ylabel("Polio")
plt.title("Grafik Jumlah Kasus Penyakit Polio")
plt.legend()
plt.grid(True) plt.show()
Kode Program 13. Visualisasi dengan Metode Single Moving Average
Kode program 13. menjelaskan tentang cara membuat visualisasi berupa grafik dengan
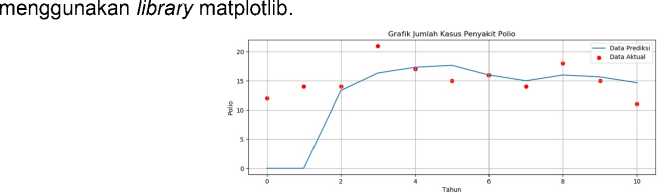
Gambar 9. Grafik Visualisasi Kasus Penyakit Polio
Gambar 4.5 menjelaskan tentang visualisasi grafik pada tahun berikutnya yaitu tahun 2021 adalah 15 kasus.
from numpy import mean, abs
actual = np.array(jumlah_df['Polio'])
pred = np.array(jumlah_df['Prediksi_Selanjutnya'])
mape= mean(abs((actual - pred)/actual))*100
Kode Program 14. Perhitungan Akurasi MAPE
Kode program 14. menjelaskan tentang menghitung tingkat akurasi peramalan metode single moving average yaitu dengan menggunakan mean absolute percentage error.
MAPE : 27.52%
Gambar 10. Hasil Tingkat Akurasi Peramalan
Gambar 10. menjelaskan tentang hasil nilai tingkat akurasi peramalan mean absolute percentage error 27.52%.
-
4.3. Support Vector Regression
Langkah-langkah perhitungan support vector regression menggunakan bahasa pemrogramaan Python dengan Pycharm sebagai medianya yang akan dijelaskan sebagai berikut.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
Kode Program 15. Import Library
Kode Program 15. menjelaskan tentang library yang digunakan dalam peramalan menggunakan metode support vector regression antara lain, Numpy, Matplotlib dan Pandas. jumlah = pd.read_csv('newpenyakit.csv') x = jumlah.iloc[:, 1:2].values y = jumlah.iloc[:, 2:3].values
x = x.reshape(-1,1)
y = y.reshape(-1,1)
Kode Program 16. Import dataset polio
Kode program 16. menjelaskan tentang import data newpenyakit.csv dengan variabel x dan y diambil dari variabel jumlah dengan nilai x yaitu 1 pada kolom kedua dataset dan y diambil dari nilai kolom ketiga pada dataset.
from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x,y, test_size=0.2,random_state=0)
train_test_split(y, shuffle=False)
Kode Program 16. Membagi Data Uji dan Data Latih
Kode program 16. menjelaskan tentang data preprocessing dengan melakukan pembagian data uji dan data latih, Langkah selanjutnya dalah melakukan feature scaling yang akan dijelaskan sebagai berikut.
from sklearn.preprocessing import StandardScaler
sc_x_ = StandardScaler()
sc_y_ = StandardScaler()
x = sc_x_.fit_transform(x)
y = sc_y_.fit_transform(y)
Kode Program 18. Feature Scaling pada dataset
Kode program 18. menjelaskan tentang data preprocessing dengan melakukan import standart scaler yang disebut juga feature scaling.
from sklearn.svm import SVR
model = SVR(kernel='rbf') model.fit(x, y)
Kode Program 19. Import library metode SVR
Kode program 19. menjelaskan import metode support vector regression dengan menggunakan kernel rbf dengan fit data menggunakan data feature scaling.
plt.scatter(sc_x_.inverse_transform(x), sc_y_.inverse_transform(y), color = 'red')
plt.plot(sc_x_.inverse_transform(x), sc_y_.inverse_transform(model.predict(x))) plt.title('Grafik Jumlah Kasus Penyakit Polio')
plt.xlabel('Tahun')
plt.ylabel('Polio') plt.show()
Kode Program 20. Visualisasi dataset polio
Kode program 20. menjelaskan tentang visualisasi data yang sudah dilakukan terhadap dataset dengan menggunakan scatter, plot, title, xlabel, dan ylabel.
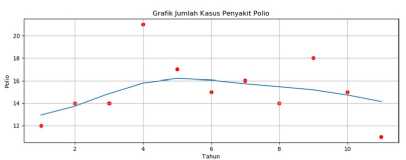
Gambar 11. Visualisasi grafik kasus penyakit polio
Gambar 11. menjelaskan tentang grafik visulisasi grafik kasus penyakit polio yang scatter berwarna merah merupakan data aktual dan plot berwarna biru merupakan data prediksi. Langkah selanjutnya mencari nilai prediksi kasus penyakit polio pada tahun 2021 yang akan dijelaskan sebagai berikut.
y_pred_ = model.predict(sc_x_.transform(np.array([[6.5]])))
y_pred_ = sc_y_.inverse_transform(y_pred) print(f'Prediksi Jumlah Kasus Penyakit Berikutnya:{y_pred_}')
Kode Program 21. Nilai prediksi polio selanjutnya
Kode program 21. menjelaskan tentang mencari hasil nilai prediksi dan melakukan print hasil jumlah kasus penyakit polio yang akan dijelaskan sebagai berikut.
Prediksi Jumlah Kasus Penyakit Berikutnya:[15.8923919]
Gambar 12. Hasil nilai prediksi jumlah kasus penyakit polio
Gambar 12. menjelaskna tentang hasil nilai prediksi jumlah kasus penyakit polio pada metode support vector regression yang bernilai 15.89 atau digenapkan menjadi 16 kasus penyakit. Selanjutnya menghitung nilai akurasi atau error yang akan dijelaskan sebagai berikut. test_x = np.asanyarray(jumlah[['Periode']]) test_y = np.asanyarray(jumlah[['Polio']]) test_y_ = sc_y.inverse_transform(model.predict(sc_x.transform(test_x)))
from numpy import abs,meanS
mape= mean(abs((test_y - test_y_)/test_y))*100 print('MAPE : %.2f%%' %mape)
Kode Program 22. Hitung nilai MAPE pada kasus penyakit polio
Kode program 22. menjelaskan tentang menghitung nilai MAPE yang hasilnya akan dijelaskan sebagai berikut.
MAPE : 14.75%
Gambar 13. Hasil nilai MAPE
Gambar 13. menjelaskan tentang nilai hasil MAPE metode support vector regression yang bernilai 14.75%.
-
4.4 Hasil
Perbandingan nilai MAPE dan hasil peramalan secara keseluruhan akan dijelaskan sebagai berikut.
Tabel 2. Perbandingan Hasil Seluruh Tingkat Akurasi Kasus Penyakit menggunakan Mean Absolute Percentage Error
|
SMA |
SVR |
Regresi | |
|
Polio |
27.52% |
14.75% |
6.91% |
|
Tuberkulosis |
22.55% |
7.59% |
6.45% |
|
HIV |
46.73% |
36.67% |
36.92% |
Tabel 2. menjelaskan tentang perbandingan hasil kesleuruhan tingkat akurasi menggunakan MAPE pada 3 kasus penyakit yang menular di Kota Bandung. Hasil keseluruhan dari peramalan kasus penyakit yang ada di Kota Bandung akan dijelaskan sebagai berikut.
Tabel 3. Hasil Keseluruhan Peramalan Kasus Penyakit
|
SMA |
SVR |
Regresi | |
|
Polio |
15 kasus |
16 kasus |
15 kasus |
|
Tuberkulosis |
2264 kasus |
2235 kasus |
2217 kasus |
|
HIV |
251 kasus |
260 kasus |
251 kasus |
Tabel 3. menjelaskan tentang keseluruhan kasus penyakit yang diprediksi pada tahun 2021 di Kota Bandung dengan metode regresi linier sederhana, single moving average, dan support vectore regression.
-
5. Kesimpulan
Simpulan yang dapat ditarik berdasarkan perumusan masalah, tujuan masalah, serta hasil pembahasan adalah hasil peramalan yang dilakukan didapatkan hasil perbandingan metode – metode yang baik digunakan dalam studi kasus ini adalah Regresi linier sederhana dan support vector regression, dimana dalam kasus penyakit polio dan tuberkulosis memiliki nilai akurasi MAPE <10% dan untuk kasus penyakit HIV memiliki nilai akurasi MAPE cukup yatiu diantara 20% sampai 50%. Hasil peramalan jumlah kasus penyakit dalam studi kasus ini pada tahun 2021 yaitu polio memiliki jumlah kasus penyakit 15 kasus, tuberkulosis memiliki jumlah kasus penyakit 2217 kasus, dan HIV memiliki jumlah kasus penyakit 260 kasus.
Daftar Pustaka
-
[1] B. H. Prakoso, "IMPLEMENTASI SUPPORT VECTOR REGRESSION PADA PREDIKSI INFLASI INDEKS HARGA KONSUMEN," MATRIK, vol. 19, pp. 155-162, 2019.
-
[2] B. Santosa and A. Umam, Data Mining dan Big Data Analytics Edisi 2, Yogyakarta: Penebar Media Pustaka, 2018.
-
[3] "Dinas Kesehatan Kota Bandung," 2010. [Online]. Available: https://dinkes.bandung.go.id/. [Accessed Juni 2021].
-
[4] Y. c. Umam, M. Kharis and S. , "Model Epidemi Seiv Penyebaran Peyakit Polio pada Populasi Tak Konstan," UNNES Journal of Mathematics, vol. 2, 2016.
-
[5] A. R. Rachman, "Penerapan Metode Moving Average dan Exponential Smoothing pada Peramalan Produksi Indsutri Garment," Jurnal Informatika, vol. Vol.5 No.1, 2018.
-
[6] A. R. Iskandar, "Prediksi Jumlah Calon Siswa/i Baru di SDN Sambirejo 01 Semarang Menggunakan Tiga Metode Forecasting," 2016.
-
[7] L. Octaviany, A. Rahayu, F. Rahman and D. Rosadi, "Pengetahuan, Sikap dan Pencegahan HIV/AIDS pada Ibu Rumah Tangga," Jurnal Kesehatan Masyarakat, vol. 11, pp. 53-58, 2015.
Discussion and feedback