Modifikasi Algoritma Ant Colony Optimization Dalam Menentukan Rute Pengisian Mesin ATM

p-ISSN: 2301-5373

e-ISSN: 2654-5101

Jurnal Elektronik Ilmu Komputer Udayana

Volume 11, No 2. November 2022

Modifikasi Algoritma Ant Colony Optimization Dalam Menentukan Rute Pengisian Mesin ATM

Putu Risky Andrean¹, I Made Widiartha², Agus Muliantara³, I Gusti Ngurah Anom Cahyadi Putra⁴, I Ketut Gede Suhartana⁵, Ngurah Agus Sanjaya ER⁵

Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana Jl. Raya Kampus Unud, Indonesia ¹[email protected] ²[email protected] ³[email protected] ⁴[email protected] ⁵[email protected] ⁶[email protected]

Abstract

The TSP problem is known as a non-deterministic polynomial-hard (NP-Hard) problem. In its solution, TSP can be solved using swarm intelligence algorithms such as Artificial Bee Colony (ABC), Partical Swarm Optimization (PSO), dan Ant Colony Optimization (ACO). In this study, TSP settlement was carried out using the ACO algorithm because the amount of data was less than 80 data. In addition, modifications were made to the ACO algorithm with the aim of optimizing the probability in node selection by put in Fuzzy C-Means algorithm into the ACO algorithm.

Based on the result application of the Modified Ant Colony Optimization algorithm, the distance covered is 105.087 Km when the parameter optimization has been carried out, with parameter values a = 5, β = 0.1, p = 0.9, number of ants = 31, dan maximum iteration = 100. Where each parameter has its own role, such as the Intensity Controlling Constant (α) which makes the ants only care about the pheromone intensity value without caring about the distance value between points so that the diversity of the paths found gets smaller when the value (α) gets bigger, Visibility Controlling Constant (β) ) which affects the diversity of routes produced by each ant where when (β) = 0 then the route chosen by each ant varies and when (β) > 0 has the possibility for the route that has been selected to be re-elected by other ants so that the diversity of routes found getting smaller, while for the Ant Track Control Constant (ρ) it has an influence in determining the next destination point when the value of gets bigger. In addition, the Modified Ant Colony Optimization algorithm has the advantage of accelerating convergence in finding the shortest route.

Keywords: Fuzzy C-Means, Modified Ant Colony Optimization, Ant Colony Optimization, Travelling Salesman Problem, Generate Route

• 1.    Pendahuluan

Travelling Salesman Problem (TSP) diibaratkan sebagai seorang kurir yang memiliku kewajiban dalam mengantarkan pesanan kepada pelanggan yang berada di suatu kota atau di sejumlah daerah. Dimana kurir tersebut memiliki ketentuan untuk mendatangi kota atau daerah yang menjadi tujuan hanya dapat dikunjungi tepat satu kali, dengan titik keberangkatan dan titik akhir berada ditempat yang sama. Salah satu hal yang menjadi suatu permasalahan dalam TSP ini yaitu bagaimana cara memperoleh rute tercepat berdasarkan jarak terpendek yang didapatkan dengan mempertimbangkan ketentuan yang telah ada sehingga kurir dapat mengunjungi seluruh pelanggannya. Oleh karena itu permasalahan TSP diketahui sebagai permasalahan yang bersifat nondeterministic polynomial-hard (NP-Hard) [1].

Permasalahan TSP dapat dilakukan dengan menggunakan algoritma Swarm Intelligence seperti Artificial Bee Colony (ABC), Partical Swarm Optimization (PSO), dan Ant Colony Optimization (ACO). Dimana dalam penelitian ini untuk menyelesaikan permasalahan TSP yang dihadapi adalah dengan menggunakan algoritma Ant Colony Optimization (ACO) guna memperoleh rute terpendek berdasarkan jarak yang dijadikan rute paling optimal. Algoritma ACO dipilih didasarkan pada hasil komparasi terhadap algoritma sejenis yang diterangkan pada artikel A Comparison Between Swarm Intelligence

Algorithm For Routing Problem [2]. Artikel tersebut membandingkan algoritma Swarm Intelligence yaitu Genetic Algorithm (GA), Ant Colony Algorithm (ACO), Particle Swarm Optimization (PSO), dan Artificial Bee Colony (ABC). Hasil dari perbandingan terhadap algoritma Swarm Intelligence tersebut menyatakan bahwa algoritma Ant Colony Optimization (ACO) memiliki performa terbaik diantara algoritma Swarm Intelligence lainnya apabila jumlah data yang digunakan saat pengujian kurang dari 80 data. Hal ini dikarenakan ACO memiliki memori, di mana semut yang optimal di masa lalu diarahkan kembali ke arah feromon yang disimpan.

Peningkatan performa dari algoritma ACO dilakukan dengan cara menambahkan algoritma FCM ke dalam algoritma ACO yang telah ada. Seperti penelitian yang dilakukan dengan judul “Clustering Algoritma Fuzzy Ant Untuk Optimalisasi Penentuan Rute Kemacetan Tanah Abang” [3]. Penelitian tersebut bertujuan untuk mengoptimisasi probabilitas dalam pemilihan node dengan menambahkan algoritma FCM ke dalam algoritma ACO sehingga kemungkinan pemilihan jalur selama siklus berlangsung secara berkelanjutan. Hasil dari penelitian tersebut dijadikan sebagai dasar penyelesaian TSP yang dihadapi oleh penulis. Selain itu terdapat beberapa penelitian terdahulu yang dijadikan sebagai acuan dalam pelaksanaan penelitian ini seperti “Modifikasi Algoritma Semut Untuk Optimasi Probabilitas Pemilihan Node Dalam Penentuan Jalur Terpendek”[4], “Penerapan Algoritma Ant System dalam Menemukan Jalur Optimal pada Travelling Salesma Problem (TSP) dengan Kekangan Kondisi Jalan”[5].

• 2.    Metodologi Penelitian
  
  2.1.    Data Penelitian

Pada penelitian ini menggunakan data primer yang didapat dari salah satu agen pengisian mesin ATM yaitu PT. Beringin Gigantara untuk Bank BRI di wilayah Denpasar. Melalui sumber tersebut didapatkan sejumlah 31 data berupa titik latitude dan longitude untuk lokasi ATM. Berdasarkan titik-titik tersebut kemudian dilakukan perhitungan jarak dari setiap titik ATM menggunakan Google MAPS Direction API sehingga didapatkan jarak tempuh dari setiap titik. Setelah mendapatkan jarak dari setiap titiknya, kemudian dilakukan perhitungan menggunakan algortima Modified Ant Colony Optimization (M-ACO). Algoritma M-ACO sendiri merupakan modifikasi terhadap Algoritma Ant Colony Optimization (ACO) dengan menyisipkan algoritma Fuzzy C-Means (FCM) kedalam algoritma ACO.

• 2.2.    Travelling Salesman Problem

Travelling Salesman Problem (TSP) merupakan permasalahan terkenal pada teori graf. Pemberian nama Travelling Salesman Problem (TSP) didasari oleh permasalahan seorang pedagang yang harus mendatangi setiap tujuan tepat satu kali kemudian kembali ke tempat keberangkatannya [6]. Kota atau tujuan digambarkan sebagai simpul (node atau vertex) dari graph, sedangkan sisi digambarkan sebagai rute penghubung antar kota. Nilai pada sisi menyatakan jarak antar kota. Dengan kata lain, permasalahan travelling salesman problem (TSP) merupakan permasalahan untuk menemukan Hamilton Circuit yang memiliki bobot paling kecil (minimum) pada suatu graph terhubung.

Terdapat dua jenis TSP, yaitu simestris dan asimetris. TSP simetris meruapakan permasalah dimana nilai atau bobot dari suatu kota A ke kota B memiliki nilai yang sama kota B ke kota A. Sedangkan untuk TSP asimetris merupakan permasalahan dimana biaya atau bobot dari kota A ke kota B memeiliki nilai yang berbeda dengan kota B ke kota A. Jumlah jalur untuk TSP asimetris adalah permutasi dari jumlah kota yang harus dikunjungi dibagi dengan jumlah kota yang harus dikunjungi, sehingga dapat

dirumuskan sebagai berikut [7]:

n! n(n-k)!

P

(1)

Dimana :

n      = jumlah seluruh kota.

k      = jumlah kota yang diseleksi.

TSP digambarkan sebagai graph lengkap dengan bobot G = (V,E), dimana V merupakan himpunan titik-titik (node atau vertex) sedangkan E merupakan kumpulan dari sisi. Setiap sisi (a, b) ϵ E adalah nilai yang merepresentasikan jarak drs atau jarak dari titik a ke titik b, dengan (a, b) ϵ V. Dalam TSP n!                                           (n-1)!

simetris memiliki (_(n_₂₎,₂J buah sisi, selain itu memiliki —^- buah tour yang mungkin.

• 2.3.    Ant Colony Optimization

Pada awalnya ACO digunakan oleh penemunya yaitu Marco Dorigo [8] untuk menyelesaikan permasalahan TSP. Dimana pada penerapannya algoritma ini meniru perilaku semut yang memiliki suatu memori yang disebut dengan tabu list. Tabu list ini bertugas untuk menyimpan seluruh tempat yang telah di kunjungi oleh semut sehingga semut tidak mengunjungi tempat yang sama lebih dari satu kali.

Peran utama dari penguapan pheromone yaitu untuk mencegahnya keadaan dimana semua semut menemukan rute yang sama secara terus menerus atau dikenal dengan stagnansi. Semua proses ini

dilakukan hingga iterasi mencapai maksimum sesuai yang telah ditentukan oleh user ataupun tidak adanya lagi perubahan pada hasil yang diberikan. Perubahan keadaan oleh Ant System ini dinamakan sebagai random roportional rule, yang dapat dituliskan dengan persamaan berikut.

Pk(_r,s) = ∣∑:^^............................................................(2)

{               0, lainnya

Dimana :

Pk(r, s) τ η(r, s) β a Mk

= Peluang pindah kota dari semut k. = Tingkat pheromone. = Kedekatan antar kota = Pengontrol visibility terhadap tingkat pheromone. = Pengontrol intensitas. = Kumpulan kota-kota yang belum terkunjungi oleh semut k

Berdasarkan rumus diatas, perubahan pada pheromone trail atau tingkat pheromone dapat terjadi secara local maupun global Perubahan pheromone secara global memiliki tujuan untuk menampilkan ruas-ruas yang terdapat dalam rute terpendek Updating pheromone terjadi apabila semua semut telah menyelesaikan satu rute dan kembali ke sarangnya Updating pheromone memiliki aturan yaitu

Dimanap ∈ [0, 1] adalah decay factor atau lebih dikenal dengan faktor penguapan dan ∆τ*_s adalah penambahan jumlah pheromone pada ruas soleh semut k. Dengan tujuan meningkatkan nilai pheromone yang berkaitan dengan lintasan yang menjanjika atau bagus. Adapun langkah – langkah dalam algoritma Ant Colony Optimization, yaitu :

• 1.    Inisialisasi parameter awal, dimana:

• a.    Intensitas jejak semut yang menandakan intensitas feromon (τ_ij)

• b.    Visibilitas jejak semut η_ij = —

^ij

• c.    Tetapan pengendali intensitas [α]

• d.    Tetapan pengendali visibilitas [β]

• e.    Tetapan pengendali jejak semut [p]

• f.    Tetapan siklus semut atau max iterasi [Q]

• 2.    Mengisi titik tujuan kedalam tabu list yang dilakukan secara acak

• 3.    Penyusunan rute kunjungan setiap semut ke setiap titik

• 4.    Menjalankan semut ke titik berikutnya dengan menggunakan persamaan probabilitas, sebagai berikut:

pk _   [^ⁱjl^a[ηij]^

^ij    ∑[τik'l^α[mk'l^β..................................................................................................

• 5.    Hitung panjang rute setiap semut (Lk) setelah satu siklus diselesaikan ^k   ^dtabu_k(n),tabu_k(1) ⁺ ∑s-1 ^dtabu_k(s),tabu._k(s+1)

Dengan dij adalah jarak antara titik i ke titik j yang dihitung berdasarkan:

dij = √(χi - Xj)² +(yi - yj)²(5)

• 6.    Pencarian rute terpendek.

• 7.    Hitung perubahan intensitas jejak semut dengan meninggalkan feromon pada lintasan yang

dilaluinya

Δτij = ∑^ιΔτk(6)

Setiap semut dihitung berdasarkan persamaan

^δ⅛=⅛(7)

^Lk

• 8.    Hitung intensitas feromon semut untuk siklus berikutnya τij = pτij + Δτij(8)

• 9.    Pemberhentian iterasi ketika jumlah siklus sudah maksimm atau konvergensi

• 2.4.    Fuzzy C- Means

Fuzzy C-Means (FCM) merupakan suatu cara pengelompokan (clustering) yang membenarkan bagian data memiliki lebih dari satu kelompok / cluster. Dimana keanggotaan sebuah data dengan nilai berupa derajat keanggotaan pada rentang nol hingga satu [9].

Fuzzy C-Means memiliki konsep dasar sebagai suatu cara untuk menentukan pusat cluster terlebih dahulu, dengan tujuan untuk menandai nilai rata-rata dari setiap clusternya atau dikenal dengan nilai derajat keanggotaan. Dalam Fuzzy C-Means awalnya pusat cluster belum akurat, agar nilai pusat cluster menjadi akurat dilakukan dengan cara mengupdate nilai cluster dari setiap data secara terus-menerus hingga memenuhi kriteria yang ditentukan. Perulangan dengan tujuan untuk mengupdate nilai cluster yang didasarkan pada minimisasi fungsi objektif yang menggambarkan jarak dari titik data yang diberikan ke pusat cluster yang terbobot oleh derajat keanggotaak titik tersebut [10]. Adapun algoritma clustering FCM, yaitu :

• 1.    Menyiapkan data yang akan di cluster berupa matriks n x p, dimana :

• n : jumlah sample data sedangkan

• p : atribut dari setiap data.

Xkj : data sampel ke-k (k = 1, 2, 3, …, n), atribut ke-j (j = 1, 2, 3, …, m) 2. Menentukan input yang dibutuhkan dalam perhitungan FCM, seperti :

• a.    Jumlah cluster

  = c

  = m

  = MaxIter

  
  

• b.  Bobot pangkat

• c.  Iterasi Maksimum

• d.    Batas error                               = f

• e.    Fungsi objektif awal                       = P0 = 0

• 3.    Pembangkinan bilangan random (μ_iki = 1,2,.,c; k — 1,2,.,nj, sebagai elemen matriks partisi

awal U.

r μ_n(^χι)  μι₂(^χ₂j.  μic(^xc)

^0=l ⋮          ⋮    -      ⋮ I(9)

L μ_n(%ι)  μι₂(x₂).  μι_c(x_c)i

• 4.    Matrik partisi pada fuzzy clustering harus memenuhi kondisi sebagai berikut :

μ_ik = [0,1];⁽1 ≤ i ≤c;1 ≤ k ≤ n)(10)

∑⅛k = i; ι≤i≤c(11)

0<∑"ι‰ = 1; 1≤k ≤n (12)

Hitung jumlah setiap kolom (atribut) : Qj= ∑=M(13)

Dengan j = 1, 2, 3, …, m. Kemudian hitung :

,_l = Hlkk

(14)

(15)

(16)

(17)

(18)

^μik    Qj

5.

6.

7.

8.

Hitung pusat cluster ke-k : Vij, dimana i = 1, 2, 3, …, c dan j = 1, 2, 3, …, m.

_v _ ∑^₁((μ_ik)^m*×kj)

^ij      ∑‰ι(μik)^m

v—- ^vH

I Vcl -  Vc_m∖

Hitung fungsi objektif pada iterasi ke-t, Pt dengan menggunakan persamaan : p_t = ∑ⁿ_k=ι∑c=ι([∑m=ι^

Hitung perubahan matriks partisi :

J∑⅛k⅛^

^μik —               21

∑f=₁[∑vaxkj-v_lj)²]v-¹

Melakukan pengecekan kondisi berakhir :

a  Jika (∖P_t - P_t-11 < f) atau (t < iterasi maksimal) maka berakhir;

b  Jika tidak, maka t = t + 1 kemudian ulang langkah keempat.

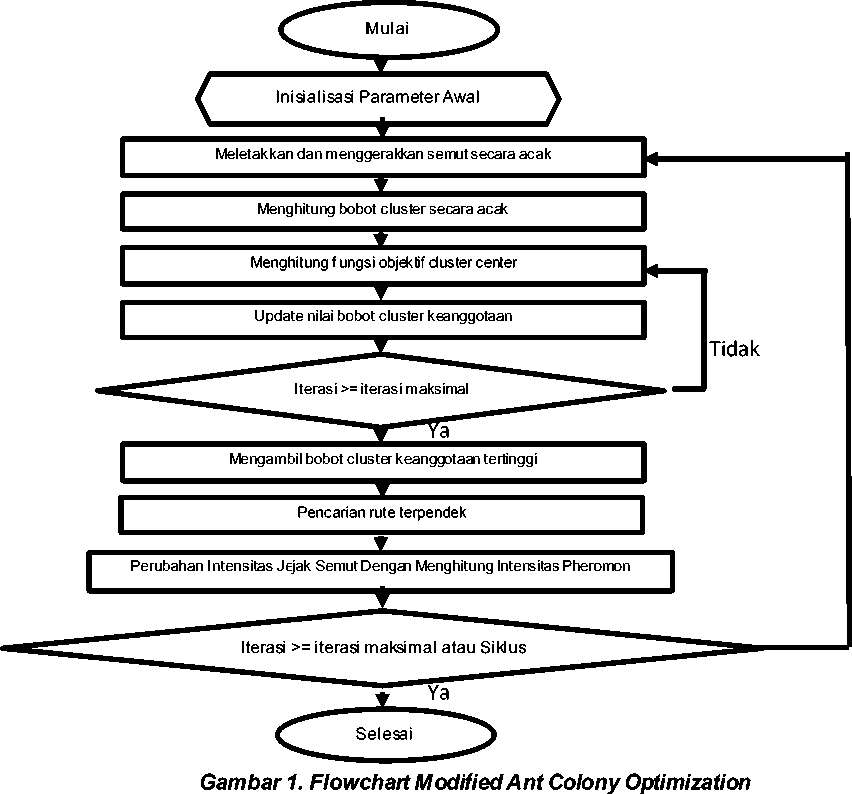
• 2.5.    Modified Ant Colony Optimization

Algoritma Modified Ant Colony Optimization merupakan modifikasi terhadap algoritma Ant Colony Optimization dengan menyisipkan algoritma Fuzzy C-Means kedalam algoritma Ant Colony Optimization [4]. Adapun langkah – langkah dari algoritma Modified Ant Colony Optimization yaitu : 1.      Menginisialisasi parameter awal algoritma Ant Colony Optimization dan Fuzzy C-Means

• 2.     Meletakkan dan menjalankan semut secara acak

• 3.     Menghitung nilai bobot cluster secara acak menggunakan algoritma Fuzzy C-Means

• 4.      Menghitung fungsi objektif cluster center Fuzzy C-Means

• 5.      Update nilai bobot cluster keanggotaan

• 6.      Melakukan pengecekan kondisi, yaitu:

• a.    Jika (∣P_t — P_t-1∣ < ξ atau (t < iterasi maksimal) maka lanjut langkah 7;

• b.    Jika tidak, t = t + 1 kemudian ulang mulai langkah 4.

• 7.      Mengambil bobot cluster keanggottan tertinggi

• 8.      Pencarian rute terpendek

• 9.      Menghitung instensitas jejak semut dengan menghitung intensitas pheromone

• 10.     Melakukan pengecekan kondisi kembali, yaitu :

• a.     Jika (iterasi >= iterasi maksimal, maka berhenti;

• b.     Jka tidak, ulangi dari langkah 3.

Tidak

• 3.    Hasil dan Pembahasan

Berdasarkan implementasi algoritma Modified Ant Colony Optimization yang telah dijelaskan sebelumnya, didapatkan hasil dari penelitian ini yaitu jarak tempuh untuk pengisian uang mesin ATM sejauh 143,12 Km. Hasil tersebut didapatkan sebelum dilakukan optimalisasi parameter, dimana parameter yang menghasilkan hasil tersebut yaitu jumlah cluster adalah 5, maximum iterasi untuk algoritma FCM adalah 100, dan pangkat pembobot (m) untuk algoritma FCM adalah 2, maximum iterasi untuk algoritma ACO adalah 100, jumlah semut yang digunakan adalah 31, jumlah titik atau kota adalah

• 31,    nilai a adalah 1, nilai β adalah 2, dan p adalah 0.9. Untuk nilai a, β, dan p didapatkan melalui bilangan random dengan rentang yang telah ditentukan seperti tabel 1.

Rentang Parameter Uji
Tetapan Pengendali Intensitas (a)	0.1; 0.3; 0.5; 1; 3; 5
Tetapan Pengendali Visibilitas (β)	0; 0.1; 0.3; 0.5; 1; 3; 5
Tetapan Pengendali Jejak Semut (p)	0.1; 0.3; 0.5; 0.7; 0.9

Tabel 1. Rentang Parameter Uji

Setelah mendapatkan hasil tersebut, kemudian dilakukan pengujian untuk mendapatkan kombinasi parameter Tetapan Pengendali Intensitas (a), Tetapan Pengendali Visibilitas (β), dan Tetapan Pengendali Jejak Semut (p) sehingga hasil keluaran berupa jarak tempuh dari algoritma Modified Ant Colony Optimization menghasilkan hasil yang optimial yaitu jarak tempuh terpendek. Adapun setting parameter Tetapan Pengendali Intensitas (a), Tetapan Pengendali Visibilitas (β), dan Tetapan Pengendali Jejak Semut (p) seperti yang terdapat pada tabel 1.

Berdasarkan pengujian tersebut didapatkan hasil kombinasi untuk parameter Pengendali Intensitas (a), Tetapan Pengendali Visibilitas (β), dan Tetapan Pengendali Jejak Semut (p) berada pada saat nilai a = 5, β = 0.1, dan p = 0.9 dengan rata-rata jarak tempuh yang dihasilkan yaitu sejauh 105.087 Km. Dimana hasil tersebut didapatkan berdasarkan pengujian yang dilakukan sebanyak lima kali dengan

hasil sebagai berikut :

a=5 dan p= 0.9

112000

^{110713           110916.4} 110573  110573  110573  110573

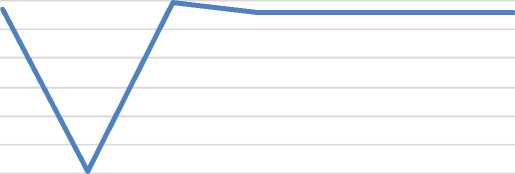
105087

111000

110000

109000

108000 CD

107000

106000 CD

105000 03

104000 K

103000

102000

β = 0     β = 0.1 β = 0.3 β = 0.5     β = 1      β = 3      β = 5

Nilai β

Gambar 2. Grafik Uji Parameter M-ACO

Berdaskarkan garfik diatas, parameter tetapan pengendali intensitas (a) mempengaruhi algoritma M-ACO dan ACO dalam memberikan keluaran dalam hal ini jarak tempuh. Dimana semakin besar nilai tetapan pengendali intensitas (a) akan menghasilkan jarak tempuh yang semakin kecil atau semakin baik, hal tersebut dikarenakan peningkatan nilai tetapan pengendali intensitas (a) membuat semut hanya memedulikan nilai intensitas pheromone tanpa memedulikan nilai jarak antar titik sehingga keragaman akan jalur yang ditemukan semakin kecil. Sehingga hal tersebut mengakibatkan konvergen dini dalam penentuan rute dan jarak tempuh

Sedangkan untuk parameter tetapan pengendali visibilitas (β) mempengaruhi keragaman rute yang dipilih oleh setiap semut. Ketika nilai tetapan pengendali visibilitas (β) = 0 maka rute yang dipilih oleh setiap semutnya beragam. Sedangkan apabila nilai tetapan pengendali visibilitas (β) > 0 maka rute yang telah terpilih oleh suatu semut memiliki kemungkinan untuk terpilih kembali oleh semut lainnya sehingga keragaman rute yang ditemukan semakin kecil.

Parameter tetapan pengendali jejak semut (p) berdasarkan pengujian tersebut memiliki pengaruh dalam menentukan titik tujuan selanjutnya. Dimana semakin besar nilai parameter tetapan pengendali

jejak semut (p) maka titik tujuan selanjutnya yang terpilih merupakan jalur terpendek yang telah ditemukan dari titik keberangkatan.

• 4.    Kesimpulan

Berdasarkan hasil pengujian parameter yang telah dilakukan, didapatkan nilai untuk setiap parameter sehingga menghasilkan hasil yang optimal untuk algoritma Modified Ant Colony Optimization yaitu α = 5, β = 0.1, p = 0.9, jumlah semut = 31, dan maksimum iterasi = 100 dengan rata-rata total jarak 105.087 Km. Dimana setiap parameter memiliki perannya masing – masing seperti Tetapan Pengendali Intensitas (a) yang membuat semut hanya memedulikan nilai intensitas pheromone tanpa memedulikan nilai jarak antar titik sehingga keragaman akan jalur yang ditemukan semakin kecil ketika nilai (a) semakin besar, Tetapan Pengendali Visibilitas (β) yang mempengaruhi keragaman rute yang dihasilkan oleh setiap semut dimana ketika (β) = 0 maka rute yang dipilih oleh setiap semutnya beragam dan ketika (β) > 0 memiliki kemungkinan untuk rute yang telah terpilih akan terpilih kembali oleh semut lainnya sehingga keragaman rute yang ditemukan semakin kecil, sedangkan untuk Tetapan Pengendali Jejak Semut (p) memiliki pengaruh dalam menentukan titik tujuan selanjutnya ketika nilai p semakin besar. Selain itu algoritma Modified Ant Colony Optimization memiliki kelebihan untuk mempercepat konvergensi dalam penemuan rute terpendek.

Daftar Pustaka

• [1]    P. I. Karmila, “Algoritma Fleury Untuk Menyelesaikan Permasalahan TSP (Traveling Salesman Problem),” J. Ilm. d’Computare, vol. Volume 8 E, 2018.

• [2]    S. Sabet, M. Shokouhifar, and F. Farokhi, “a Comparison Between Swarm Intelligence Algorithms for Routing Problems,” Electr. Comput. Eng. An Int. J., vol. 5, no. 1, 2016, doi: 10.14810/ecij.2016.5102.

• [3]    E. W. Ambarsari and S. Khotijah, “Clustering Algoritma Fuzzy Ant Untuk Optimalisasi Penentuan Rute Kemacetan Tanah Abang,” Comput. J. Comput. Sci. Inf. Syst., vol. 1, no. 2, p. 187, 2017, doi: 10.24912/computatio.v1i2.1015.

• [4]    E. W. Ambarsari, “Modifikasi Algoritma Semut untuk Optimasi Probabilitas Pemilihan Node dalam Penentuan Jalur Terpendek,” STRING (Satuan Tulisan Ris. dan Inov. Teknol., vol. 2, no. 2, p. 193, 2017, doi: 10.30998/string.v2i2.2106.

• [5]    A. A. Ismail and S. Herdjunanto, “Penerapan Algoritma Ant System dalam Menemukan Jalur Optimal pada Traveling Salesman Problem ( TSP ) dengan Kekangan Kondisi Jalan,” vol. 1, no. 3, pp. 1–6, 2012.

• [6]    B. P. Silalahi, N. Fathiah, and P. T. Supriyo, “Use of Ant Colony Optimization Algorithm for Determining Traveling Salesman Problem Routes,” J. Mat. “MANTIK,” vol. 5, no. 2, pp. 100– 111, 2019, doi: 10.15642/mantik.2019.5.2.100-111.

• [7]    Fitiyani, Y. Away, and T. A.Gani, “Pengaruh Inisialisasi Populasi Random Search Pada

Algoritma Berevolusi Dalam Optimasi Travelling Salesman Problem (TSP),” J. Nas. Komputasi dan Teknol. Inf., vol. 1. No.2, pp. 49–55, 2018.

• [8]    M. Dorigo and T. Stützle, Handbook of Metaheuristics; Ant colony optimization: Overview and recent advances, vol. 272. 2019.

• [9]    W. Sanusi, A. Zaky, and B. N. Afni, “Analisis Fuzzy C-Means dan Penerapannya Dalam Pengelompokan Kabupaten/Kota di Provinsi Sulawesi Selatan Berdasarkan Faktor-faktor Penyebab Gizi Buruk,” J. Math. Comput. Stat., vol. 2, no. 1, p. 47,  2020, doi:

10.35580/jmathcos.v2i1.12458.

• [10]    S. Tri Kismanti and A. Ard Maidah, “Penentuan Kelompok Jaringan Logistik pada Wilayah Kepulauan menggunakan Fuzzy C-Means,” Borneo Eng. J. Tek. Sipil, vol. 2, no. 2, p. 76, 2018, doi: 10.35334/be.v2i2.615.

This page is intentionally left blank.

308