Diagnosis Penyakit Retinopati Diabetes Menggunakan SVM dengan Optimasi Algoritma Genetika

p-ISSN: 2301-5373

e-ISSN: 2654-5101

Jurnal Elektronik Ilmu Komputer Udayana

Volume 11, No 3. February 2023

Diagnosis Penyakit Retinopati Diabetes Menggunakan SVM dengan Optimasi Algoritma Genetika

Ida Bagus Weda Baskara Adi Putra^a1, Luh Gede Astuti^a2, AAIN Eka Karyawati^a3 I Wayan Santiyasa^a4, Cokorda Rai Adi Pramartha^a5, I Gede Santi Astawa^a6

^aProgram Studi Informatika, Universitas Udayana Kuta Selatan, Badung, Bali, Indonesia ¹[email protected] ²[email protected] ³[email protected] ⁴[email protected] ⁵[email protected] ⁶[email protected]

Abstract

Diabetes mellitus is a non-communicable disease that is widely infected in the community. People with diabetes mellitus often do not realize that they are infected and are only known after complications occur. Diabetic retinopathy is one of the complications of diabetes mellitus. Diabetic retinopathy occurs when the vessels in the retina are damaged, causing visual disturbances. Diabetic retinopathy is divided into 2 stages, namely Non-Proliferative Diabetic Retinopathy (NPDR) and Proliferative Diabetic Retinopathy (PDR).This study diagnoses diabetic retinopathy using classification methods, namely SVM and GLCM as feature extraction methods. In addition, this study adds an optimization method, namely genetic algorithms to determine the optimal parameters for SVM. The amount of data used is 885 images with 3 labels, namely Normal, NPDR, and PDR. The test results in this study, SVM with genetic algorithms get better results than SVM without optimization. In SVM without F1 optimization the highest score was obtained at 0.7372 while in SVM with F1 optimization the highest score was obtained at 0.7578 with an increase in the percentage of F1 Score by 2.06%.

Keywords: Diabetic Retinopathy, Diagnosis, SVM, GLCM, Genetic Algorithm, Parameter

• 1.    Pendahuluan

Penyakit diabetes terus meningkat prevelansinya diseluruh dunia. Berdasarkan data International Diabetes Federation (IDF) penyandang diabetes didunia sebanyak 463 juta orang dewasa pada awal tahun 2020 dengan prevalensi global mencapai 9,3 persen. Di Indonesia angka penderita diabetes mencapai 10,8 juta per tahun 2020 dan menempati peringkat ke-7 dari 10 negara pendertia diabetes terbanyak berdasarkan data International Diabetes Federation [1]. Penyakit diabetes melitus terjadi akibat kurangnya insulin di dalam tubuh sehingga kadar gula akan meningkat [2].

Penyandang diabetes melitus sering tidak menyadari bahwa ia terjangkit dan baru diketahui setelah terjadinya komplikasi[3]. Komplikasi dari penyakit diabetes melitus salah satunya adalah retinopati diabetes. Retinopati diabetes adalah gangguan pada mata akibat pembuluh darah pada retina rusak. Retinopati diabetes berpotensi menyebabkan kebutaan jika tidak diagnosis sedini mungkin.

Diagnosis retinopati diabetes dapat dilakukan dengan menggunakan metode klasifikasi. Klasifikasi adalah metode pengelompokan data berdasarkan label/kelas yang ada. Penelitian mengenai klasifikasi penyakit retinopati diabetes sebelumnya sudah pernah dilakukan pada tahun 2018. Dimana dalam penelitian tersebut dapat mengindenfikasi pasien pengidap retinopati diabetes melalui citra fundus retina. Metode klasifikasi yang digunakan terdapat 4, dimana metode random forest memperoleh hasil terbaik dan metode ekstraksi fitur yang digunakan adalah GLCM [4]. Selain itu penelitian lainnya dengan menggunakan naïve bayes dan GLCM juga dapat melakukan klasifikasi retinopati diabetes [5].

Pada penelitian ini menggunakan Support Vector Machine (SVM) pada metode klasifikasi dan GLCM pada metode ekstraksi fitur. Pada metode SVM terdapat parameter yang harus ditentukan seperti parameter C dan parameter lainnya. Penentuan nilai parameter yang tepat akan berpengaruh terhadap model SVM yang dihasilkan [6].

Penentuan parameter pada SVM biasanya dilakukan manual dengan cara mencoba setiap kombinasi nilai dan akan membutuhkan waktu lebih lama. Dari permasalahan tersebut diperlukan suatu teknik yang dapat mengoptimasi pemilihan nilai parameter tersebut dengan cara otomatis yaitu dengan menggunakan algoritma genetika.

Penelitian mengenai SVM dengan algoritma genetika sebagai optimasi sebelumnya sudah pernah dilakukan pada tahun 2019. Dimana pada penelitian tersebut membandingkan SVM dengan optimasi dan tanpa optimasi dimana SVM dengan optimasi memperoleh akurasi lebih baik dibandingkan dengan metode SVM tanpa optimasi [7]. Selain itu terdapat juga penelitian lainnya yang menggunakan algoritma genetika sebagai penentuan nilai parameter optimal pada SVM pada tahun 2017. Pada penelitian tersebut penentuan nilai parameter SVM dengan algoritma genetika memperoleh hasil lebih baik [8].

Dari penjabaran diatas maka dalam penelitian ini akan menggunakan algoritma genetika dalam menentukan parameter pada SVM untuk diagnosis penyakit retinopati diabetes berdasarkan ciri tekstur pada citra fundus retina dengan GLCM.

• 2.    Metode Penelitian
  
  2.1.  Pengumpulan Data

Data yang digunakan pada penelitian ini adalah data sekunder dari APTOS 2019 Blindness Detection resized version yang didapat dari kaagle.com. Jumlah dataset yang digunakan adalah 800 data citra fundus retina. Dimana dataset yang didapatkan akan dibagi menjadi 3 label yaitu Normal, Non Proliferative Diabetic Retinopathy (NPDR) , dan Proliferative Diabetic Retinopathy (PDR). NPDR adalah fase awal retinopati diabetik yang ditandai dengan adanya microaneurisma, pendarahan, dan eksudat pada retina. PDR adalah fase selanjutnya yang ditandai dengan adanya neovaskularisasi dan pendarahan pada vitreous [9].

• 2.2.    Preprocessing

Seperti terlihat pada Gambar 1, tahap preprocessing diawali dengan melakukan cropping untuk menghilangkan area hitam. Setelah melalui tahap cropping, setiap data citra diresize kedalam dimensi 200x200 piksel. Kemudian setiap citra yang telah diresize dikonversi ke greyscale. Setelah itu setiap citra difilter menggunakan median filter yang bertujuan untuk menghilangkan noise. Setelah noise dihilangkan citra ditingkatkan menggunakan metode CLAHE. Contrast Limited Adaptive Histogram Equalization (CLAHE) digunakan untuk memperoleh kontras yang lebih baik sehingga fitur eksudat, mikroaneurisma dan pembuluh darah lebih terlihat jelas. Dilanjutkan tahap eliminasi optic disk. Eliminasi optic disk dilakukan dengan cara mencari nilai intesitas maksimum pada citra karena optic disk pada retina biasanya memiliki nilai intesitas paling tinggi. Kemudian nilai dari intesitas tersebut dapat digunakan untuk mencari letak titik dari nilai intesitas tersebut. Pada titik tersebut dapat menggunakan masking dengan objek lingkaran untuk menghilangkan optic disk.

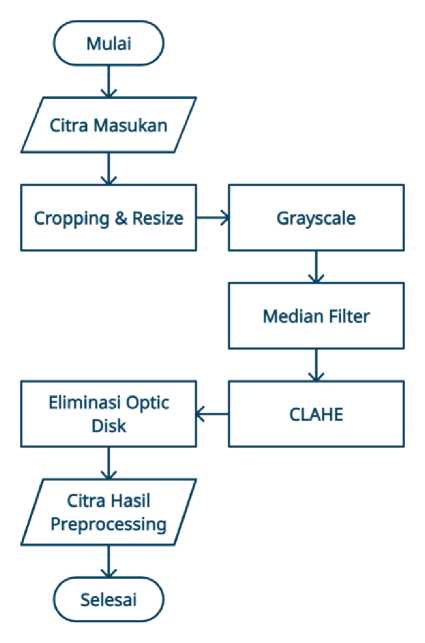
Gambar 1. Preprocessing Citra

• 2.3.    Ekstraksi Fitur dengan GLCM

Setelah tahap preprocessing citra dilanjutkan ke tahap ekstraksi fitur menggunakan GLCM, seperti terlihat pada Gambar 2.

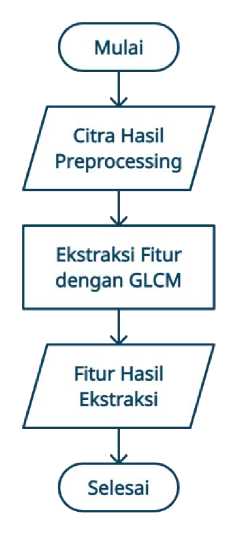
Gambar 2. Tahap Ekstraksi Fitur

Gray Level Co-Occurance Matrix (GLCM) adalah sebuah metode yang dapat digunakan dalam menganalisis dan mengekstrasi fitur pada sebuah citra. GLCM bekerja dengan membuat sebuah matriks yang digunakan untuk menggambarkan hubungan antara dua piksel pada jarak dan arah yang sudah ditentukan dalam suatu gambar [10]. Ekstrasi fitur pada GLCM dilakukan dalam 4 arah sudut yaitu 0, 45, 90, 135.

Adapun beberapa fitur yang dapat diekstraksi oleh GLCM, yaitu

a. Contrast

Contrast adalah fitur yang digunakan untuk mengukur tingkat perbedaan intensitas pada citra.

Contrast = ∑*=₁∑‰(i - j)²P_ij(1)

• b.    Correlation

Correlation adalah fitur untuk mengukur korelasi antar pixel pada citra.

Correlation = _X»_1E* ₁<!-i<⅛S_i*^j

^j

• c.    Energy

Energy adalah fitur untuk mengukur keseragaman intensitas pada citra.

Energy = ∑∙=ι ∑‰ι p²ij(3)

• d.    Entropy

Entropy adalah fitur untuk mengukur ketidakaturan distribusi intensitas suatu citra.

Entropy = ∑^ι ∑f=ι p_ij log₂P_ij(4)

• e.    Homogeneity

Homogeneity adalah untuk mengukur kehomogenan variasi intensitas suatu citra.

Homogeneity = ∑⅛ι ∑‰ -⅛^j-(5)

^1+|t-j|

• 2.4.    Min – Max Normalization

Selanjutnya nilai hasil ekstraksi fitur GLCM ditranformasi ke skala 0 sampai 1 menggunakan metode min – max. Berikut rumus dari metode min - max :

v’ = —v mm_A— (new_maxA — new_minA) + new_minA              (6)

max A- mιnA

Keterangan :

v′ : Nilai data yang telah dinormalisasi

v : Nilai data yang belum dinormalisasi

maxA : Nilai tertinggi dari data

minxA : Nilai terkecil dari data

new_maxA : Nilai tertinggi data baru

new_minA : Nilai terkecil data baru

• 2.5.    Penentuan Parameter Optimal pada SVM dengan Algoritma Genetika

Proses penentuan parameter optimal pada SVM dilakukan dengan menggunakan algoritma genetika. Flowchart dari proses penentuan nilai parameter SVM dengan algoritma genetika dapat dilihat pada Gambar 3.

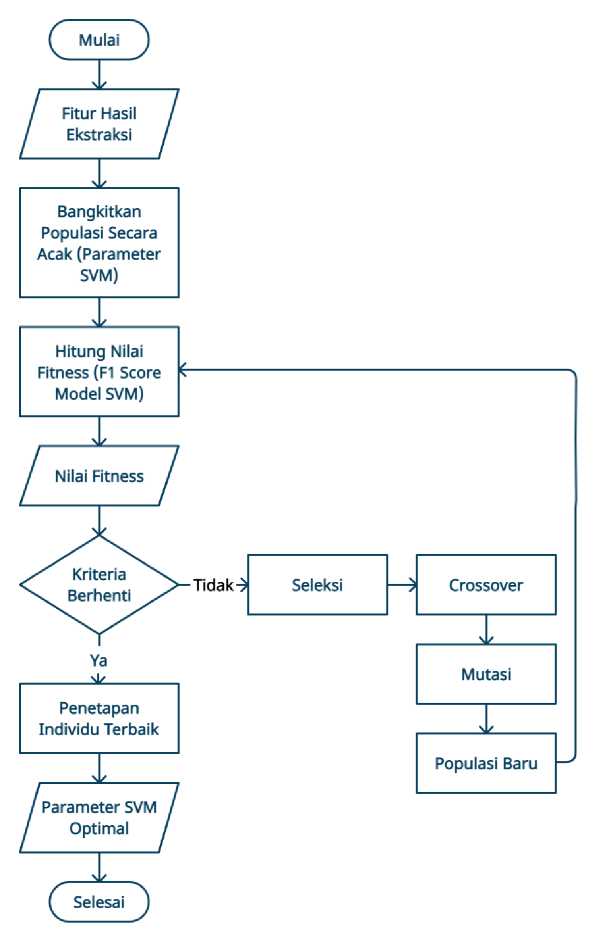
Gambar 3. Flowchart penentuan parameter SVM

• 2.5.1.    Algoritma Genetika

Algoritma genetika adalah algoritma pencarian yang berlandaskan pada prinsip seleksi alam. Algoritma genetika dapat digunakan sebagai solusi untuk permasalahan optimasi pada pencarian.

Terdapat struktur secara umum dari algoritma genetika, sebagai berikut [11].

• 1.    Membangkitkan populasi awal

Tahapan awal dalam algoritma genetika dimulai dengan pembangkitkan populasi yang dibentuk dari sekumpulan N individu secara random. Setiap individu akan memiliki sebuah kromosom. Individu - individu ini mempresentasikan sekumpulan solusi yang diinginkan. Dalam penelitian ini jumlah kromosom setiap individu adalah sama dengan jumlah parameter pada SVM yang ingin dioptimalkan

• 2.    Evaluasi Fitness

Setiap individu pada populasi akan dilakukan evaluasi dengan menghitung nilai fitnessnya. Nilai fitness dalam penelitian ini adalah F1 Score dari model klasifikasi SVM. Nilai F1 Score masing – masing individu akan dievaluasi sampai terpenuhi kriteria berhenti, jika tidak terpenuhi populasi baru akan dibentuk.

• 3.    Seleksi

Proses ini menyeleksi individu yang akan digunakan pada proses crossover nanti sebagai orang tua. Roulette – Wheel merupakan salah satu metode yang dapat digunakan untuk melakukan proses seleksi. Langkah pertama untuk menggunakan seleksi Roulette – Wheel adalah membuat interval nilai kumulatif dari rank nilai fitnes masing – masing individu dibagi total rank semua individu. Langkah selanjutnya membangkitkan bilangan random. Jika bilangan random berada dalam interval nilai kumulatif suatu individu maka individu tersebut akan dipilih.

• 4.    Crossover

Orang tua yang telah dipilih pada proses seleksi akan dilakukan crossover (kawin silang) untuk menghasilkan individu baru. Tetapi sebelum itu ditentukan terlebih dahulu apakah crossover akan dilakukan atau tidak dengan membangkitkan bilangan random. Jika bilangan random yang dibangkitkan lebih kecil dari probabilitas crossover (pc) yang ditentukan maka crossover dilakukan.

• 5.    Mutasi

Mutasi merupakan proses mengubah nilai gen dalam suatu individu. Proses mutasi dilakukan jika kondisi berikut terpenuhi yaitu bilangan random yang dibangkitkan suatu individu lebih kecil dari probabilitas mutasi (pm) yang telah ditentukan.

• 2.5.2.    Support Vector Machine (SVM)

SVM adalah metode klasifikasi yang bekerja dengan cara membuat sebuah garis pemisah untuk memisahkan kelas yang berbeda yaitu +1 dan -1. Garis pemisah ini disebut dengan hyperplane.

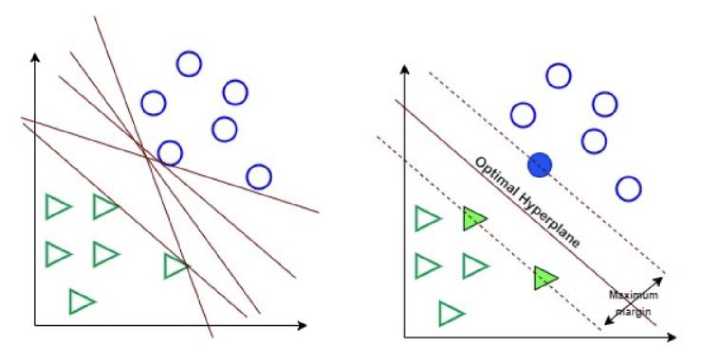
Gambar 4. Hyperplane optimal SVM (Sumber : www.dicoding.com)

Untuk mencari hyperplane yang optimal dapat ditemukan dengan mengukur atau mencari margin dari hyperplane tersebut yang maksimal. Jarak antara hyperplane dengan support vector pada masing – masing kelas disebut dengan margin [12]. Pada Gambar 4, segita berwarna hijau dan lingkaran berwarna biru merupakan sebuah support vector.

SVM dapat digunakan untuk melakukan klasifikasi pada kasus linear dan non linear. Pada kasus non linear SVM menggunakan konsep kernel pada ruang berdimensi tinggi.

Berikut merupakan fungsi kernel pada SVM non linear :

• 1.    Kernel Linear

K(x, y) = x.y                                                           (7)

Keterangan :

• x, y = fitur data

• 2.    Kernel Polynomial

K(x, y) = (γ(x. y) + r)^d                                                   (8)

Keterangan : x, y = fitur data r = koefisien polynomial d = derajat polynomial γ = control variabel

• 3.    Kernel Radial Basis Function (RBF)

K(x, y) = exp (-γ∣∣x-y∣∣²)                                                  (9)

Keterangan : x, y = fitur data γ = control variabel

Untuk melakukan klasifikasi menggunakan SVM dapat menggunakan persamaan berikut : u = ∑=ιyιaiK(Xi,x~)-b                                (10)

Keterangan : u = hasil klasifikasi y∣ = kelas ke - i (+1 atau -1) «i = support vector dari data ke - i K(xi,x) = fungsi kernel b = nilai bias

Nilai support vector dan bias dapat ditemukan pada proses pembelajaran SVM. Metode pembelajaran SVM yang dapat digunakan adalah metode Sequential Minimal Optimization (SMO).

• 3.    Hasil dan Pembahasan

Pengujian dilakukan dengan menghitung nilai rata - rata F1 Score menggunakan k fold cross validation pada proses klasifikasi SVM dengan algoritma genetika. Kemudian dibandingkan dengan SVM tanpa optimasi. Nilai k yang digunakan pada k fold cross validation adalah 5. Dan kernel SVM yang akan diuji adalah kernel polynomial. Terdapat beberapa parameter pada kernel polynomial yakni C, gamma, r dan degree.

• 3.1.    Pengujian Tanpa Optimasi

Pada pengujian ini dilakukan pengujian model SVM kernel polynomial dengan menggunakan beberapa kombinasi nilai parameter yang telah ditentukan.

Tabel 1 menyajikan hasil k fold cross validation untuk model SVM dengan kernel polynomial menggunakan 16 kombinasi nilai parameter. Setiap kombinasi nilai parameter memperoleh nilai rata -rata F1 Score yang berbeda – beda. Dimana pada tabel tersebut terlihat nilai rata – rata F1 Score terbaik diperoleh sebesar 0.7372 dengan mengunakan kombinasi nilai parameter degree = 4, r = 1, gamma = 1 dan C = 0.5.

Tabel 1. Hasil pengujian SVM tanpa optimasi pada kernel polynomial

Degree	r	gamma	C	F1 Score
2	1	0.50	0.50	0.6432
2	1	0.50	1.00	0.6924
2	1	1.00	0.50	0.7222
2	1	1.00	1.00	0.6992
3	1	0.50	0.50	0.6740
3	1	0.50	1.00	0.6725
3	1	1.00	0.50	0.6970
3	1	1.00	1.00	0.7092
4	1	0.50	0.50	0.6547
4	1	0.50	1.00	0.7276
4	1	1.00	0.50	0.7372
4	1	1.00	1.00	0.7283
5	1	0.50	0.50	0.7362
5	1	0.50	1.00	0.7016
5	1	1.00	0.50	0.7117
5	1	1.00	1.00	0.7210

• 3.2.    Pengujian SVM dengan Optimasi

Pada pengujian SVM dengan optimasi terdapat 3 pengujian yaitu pengujian nilai probabilitas mutasi, nilai probabilitas crossover dan jumlah populasi.

• 3.2.1.    Pengujian Probabilitas Mutasi

Pengujian probabilitas mutasi dilakukan 4 kali dimana nilai yang diuji 0.1, 0.2, 0.3, 0.4 dengan menggunakan nilai probabilitas crossover 0.6 dan jumlah populasi 10.

Tabel 2 menyajikan nilai parameter yang dihasilkan dari algoritma genetika serta hasil k fold cross validation untuk model SVM dengan kernel polynomial. Pada tabel tersebut terlihat nilai rata - rata F1 score terbaik adalah 0.7578 dengan nilai parameter degree = 5, r = 0.40586, gamma = 0.59903 dan C = 0.43708. Nilai parameter ini dihasilkan dari algoritma genetika ketika menggunakan nilai probabilitas mutasi 0.2.

Tabel 2. Hasil pengujian nilai mutasi algoritma genetika pada SVM kernel polynomial

Pm	d	r	Gamma	C	F1 Score
0.1	5	0.29757	0.55123	0.68195	0.7455
0.2	5	0.40586	0.59903	0.43708	0.7578
0.3	4	0.69073	0.64586	0.69073	0.7411
0.4	5	0.57659	0.76878	0.13953	0.7437

• 3.2.2.    Pengujian Probabilitas Crossover

Pengujian probabilitas crossover dilakukan 4 kali dimana nilai yang diuji 0.6, 0.7, 0.8, 0.9 dengan menggunakan nilai probabilitas mutasi 0.1 dan jumlah populasi 10.

Tabel 3 menyajikan nilai parameter yang dihasilkan dari algoritma genetika serta hasil k fold cross validation untuk model SVM dengan kernel polynomial. Pada tabel tersebut terlihat nilai rata - rata F1 score terbaik adalah 0.7577 dengan nilai parameter degree = 5, r = 0.12197, gamma = 0.76390 dan C = 0.17465. Nilai parameter ini dihasilkan dari algoritma genetika ketika menggunakan nilai probabilitas crossover 0.7.

Tabel 3. Hasil pengujian nilai crossover algoritma genetika pada SVM kernel polynomial

Pc	d	r	Gamma	C	F1 Score
0.6	5	0.29757	0.55123	0.68195	0.7455
0.7	5	0.12197	0.76390	0.17465	0.7577
0.8	5	0.40489	0.81756	0.17953	0.7460
0.9	5	0.69854	0.89756	0.39708	0.7415

• 3.2.3.    Pengujian Jumlah Populasi

Jumlah populasi yang diuji adalah 10, 20, 30, 40 dengan menggunakan probabilitas crossover 0.6 dan probabilitas mutasi 0.1.

Tabel 4 menyajikan nilai parameter yang dihasilkan dari algoritma genetika serta hasil k fold cross validation untuk model SVM dengan kernel polynomial. Pada tabel tersebut terlihat nilai rata - rata F1 score terbaik adalah 0.7524 dengan nilai parameter degree = 4, r = 0.90829, gamma = 0.95804 dan C = 0.81366. Nilai parameter ini dihasilkan dari algoritma genetika ketika menggunakan jumlah populasi 40.

Tabel 4. Hasil pengujian jumlah populasi algoritma genetika pada SVM kernel polynomial

Pop	d	r	Gamma	C	F1 Score
10	5	0.29757	0.55123	0.68195	0.7455
20	4	0.40099	0.65561	0.92878	0.7404
30	4	0.76976	0.93170	0.32001	0.7405
40	4	0.90829	0.95804	0.81366	0.7524

• 3.3.    Perbandingan Tanpa Optimasi dan Dengan Optimasi

Berikut perbandingan nilai F1 Score tertinggi yang diperoleh dari masing - masing pengujian SVM tanpa optimasi dan dengan optimasi.

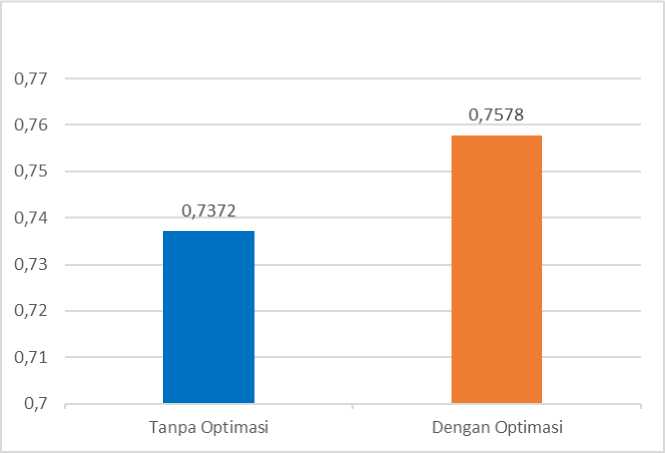
Gambar 5. Perbandingan F1 Score tanpa optimasi dan dengan optimasi

Berdasarkan pada Gambar 5, SVM dengan optimasi memperoleh hasil lebih baik dibandingkan tanpa optimasi dalam diagnosis retinopati diabetik berdasarkan ciri tekstur pada citra fundus retina pada penelitian ini. SVM tanpa optimasi memperoleh F1 Score sebesar 0.7372 sedangan dengan optimasi F1 Score yang diperoleh sebesar 0.7578. Dengan menggunakan optimasi, persentase F1 Score yang diperoleh meningkat sebesar 2,06 %.

• 4.    Kesimpulan

Pada pengujian algoritma genetika, perubahan parameter probabilitas crossover, mutasi dan jumlah populasi berpengaruh terhadap nilai F1 Score yang diperoleh. Jika nilai probabilitas crossover dan mutasi semakin besar, F1 Score yang diperoleh cenderung menurun. Sedangkan pada jumlah populasi, jika nilainya semakin besar, F1 Score yang diperoleh cenderung meningkat.

Model klasifikasi SVM dengan optimasi menghasilkan nilai F1 Score yang lebih tinggi dibandingkan dengan tanpa optimasi. Pada SVM tanpa optimasi F1 score tertinggi diperoleh sebesar 0.7372 sedangkan pada SVM dengan optimasi F1 score tertinggi diperoleh sebesar 0.7578 dengan kenaikan persentase F1 Score sebesar 2,06 %.

Daftar Pustaka

• [1]    IDF, IDF Diabetes ATLAS, 9^th ed, Belgia: International Diabetes Federation, 2019.

• [2]    D. Hardianto, “Telaah Komprehensif Diabetes Melitus: Klasifikasi, Gejala, Diagnosis, Pencegahan, Dan Pengobatan” Bioteknologi & Biosains Indonesia, vol. 7, no. 2, p. 304 – 317, 2020.

• [3]    Kemenkes RI, “Profil Kesehatan Indonesia 2014”, Jakarta: Kemenkes RI, 2014.

• [4]    A. Anitha dan T. Sridevi, “Classifying Diabetic Retinopathy In Retinal Images Utilizing GLCM And Evolutionary PSO Features” International Journal of Computer Engineering and Applications, vol 12, no. 3, p. 168 – 178, 2018.

• [5]    Erwin, A. L. Nurjanah, S. D. Noviyanti dan Yurika, “Klasifikasi Penyakit Diabetik Retinopathy dengan Metode Naïve Bayes pada Citra Retina” Annual Research Seminar, vol. 4, no. 1, p. 126 – 131, 2018.

• [6]    L. C. Huang dan J. C. Wang, “A Ga-based Feature Selection and Parameters Optimization for Support Vector Machines” Expert Systems with Application, vol. 31, no. 2, p. 231 – 240, 2006.

• [7]    H. Harfani dan A. Maulana, “Penerapan Algoritma Genetika pada Support Vector Machine Sebagai Pengoptimasi Parameter untuk Memprediksi Kesuburan” Jurnal Teknik Informatika STMIK Antar Bangsa, vol. 5, no. 1, p. 51-59, 2019.

• [8]    J. Manurung, H. Mawengkang dan E. Zamzani, “Optimizing Support Vector Machine Parameters with Genetic Algorithm for Credit Risk Assessment” Journal of Physics, vol. 930, no. 1, p. 1 – 5, 2017.

• [9]    A. S. Soelistijo, Pengelolaan dan Pencegahan Diabetes Melitus Tipe 2 Dewasa di Indonesia, Jakarta: PB PARKENI, 2019.

• [10]    Rizal, "Analisis Gray Level Co-Occurrence Matrix (GLCM) Dalam Mengenali Citra Ekspresi Wajah" Jurnal Mantix, vol. 3, no. 2, pp. 31-38, 2019.

• [11]    P.G.L.N Suwirmayanti, M. I. Sudarsana dan S. Darmayasa, “Penerapan Algoritma Genetika Untuk Penjadwalan Mata Pelajaran” Journal of Applied Intelligent System, vol. 1, no. 3, p. 220-233, 2016.

• [12]    M. I. Rosadi, C. B. Sanjaya dan L. Hakim, “Klasifikasi Diabetic Retinopathy Menggunakan Seleksi Fitur Dan Support Vector Machine” Jurnal Rekayasa Sistem Komputer System, vol. 1, no. 2, p. 109 - 117, 2018.

This page is intentionally left blank.

468