Gaussian Filtering Method to Remove Noise in Images

p-ISSN: 2301-5373

e-ISSN: 2654-5101

Jurnal Elektronik Ilmu Komputer Udayana

Volume 10 No. 1, August 2021

Gaussian Filtering Method to Remove Noise in Images

I Dewa Gede Rama Satya^a1, I Made Widiartha, S.Si., M.Kom.^a2

^aInformatics Department, Udayana University Bali, Indonesia

¹dewarama.satya@gmail.com

²madewidiartha@unud.ac.id

Abstract

Capturing every moment is not taboo in this era. One way to capture the moment is to use a photo, but the results are often unsatisfactory. Noise, is one of the many causes of unsatisfactory results. Noise is a disturbance caused by digital data storage received by the image data receiver which can interfere with image quality. Noise can be caused by physical (optical) disturbances in the image capturing device, such as dust on the camera lens or due to improper processing. To get rid of this noise, you can use various methods, of which Gaussian Filtering is one of them. In this research, we will implement it using Matlab. The type of file used is a photo that has a jpg format and has noise above 75%. After doing image processing, it shows the results of the image which initially has noise and after the image quality improvement process is carried out, the image quality is clearer and the noise decreases.

Keywords: Image Processing, Noise, Image, Gaussian Filter, Photographic

• 1.    Introduction

The terms photographic and non-photographic images are essentially remote sensing images without reducing the quality of the object being targeted. So, in this corridor, the uniform quality of the image structure will be exactly the same without having the research person come into contact with the object. Especially in this day and age with the sophistication of technology, the retrieval can be done by air, land, or sea. Basically, the image is divided into various types, including: ultraviolet photos, black and white pannomatic photos, color panchromatic photos, orthochromatic photos, black and white infrared photos, and multispectral photos.

The activity of capturing moments with photos is common in today's era. Photo is a still image, both color and black and white, which is produced by a camera that records an object or event or situation at a certain time. When taking pictures and seeing the results, there is an object that makes you feel curious about that object. This usually happens when an object is moving too fast or the object's presence is too far away, especially when the camera is of low quality.

This is the basis for the author to be able to create a system that can make the objects captured in the photo image sharper or clearer. This method aims to make objects that initially are less clear, after processing it becomes sharper so that the object can be identified in the end.

• 2.    Reseach Methods

This research takes the title of Gaussian Filtering Method to Remove Noise in Images. The system design will be illustrated in Figure 1:

Input Image

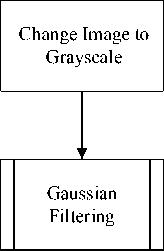
Image Result

Figure 1. Research Design

After changing the image to grayscale, the next step is to determine the mask. The mask that is often used for image refinement is the Gaussian smoothing mask. The weight on the Gaussian smoothing mask follows the normal distribution as stated in the equation below:

1    -(m²+n²)

h(m,ri) = -----e 2σ²

2πσ²

Where:

• a.    σ is the standard deviation value of the normal distribution used. The greater the value of σ, the more neighboring points are included in the calculation.

• b.    x and y are the coordinates of the mask where the coordinates (0,0) are the positions of the midpoint of the mask that have the greatest / highest value.

• c.    π is a constant with the value 3.14.

• d.    e is a natural number constant with the value 2, 718281828.

In this research, using data in the form of the value of each pixel and noise in the image image. In order to find the value for each image pixel, you can use the following sources: c=imread('coba.jpg','jpg');

asci=uint8(c)

134 133	133 132	133 132	133 132	134 134	134 134	134 134	134 134	134 134	134 134	134 134	134 134	138 137	137 136	135 134	133 132	132 131	133 132	134 133	135 134
132	132	132	132	135	135	135	135	135	135	135	135	135	135	134	133	133	133	134	134
134	134	133	133	135	135	135	135	135	135	135	135	134	134	135	136	136	136	135	135
136	135	135	135	135	135	135	135	135	135	135	135	128	130	132	133	134	134	132	132
137	135	133	133	133	134	136	137	137	137	135	134	136	136	136	136	135	135	135	135
133	131	129	129	128	130	132	134	136	136	136	136	132	132	132	132	132	132	132	132
130	128	128	I 128	128	129	131	132	132	133	133	132	129	129	129	129	127	127	127	127
127	125	125	126	133	133	132	131	130	129	128	128	125	125	125	125	125	125	125	125
126	125	125	127	132	132	131	129	128	128	127	127	125	125	125	125	123	123	123	123
123	122	123	125	127	127	127	127	128	130	131	132	123	123	123	123	121	121	121	121
120	120	121	123	123	123	122	123	124	127	129	130	122	122	122	122	120	120	120	120
116	116	117	119	125	124	122	121	122	123	125	126	119	119	119	119	119	119	119	119
119	119	119	120	119	119	119	118	117	116	114	113	115	114	112			112	114	115
116	116	115	115	116	116	116	116	115	113	112		114	113	112			112	113	114
112								IlO	109	107	107	111		110	109	109	IlO	111	111
108	109	109	109	107	108	108	108	108	107	105	105	108	108	108	108	108	108	108	108
105	106	107	107	103	103	104	104	104	103	102	102	102	102	103	103	103	103	102	102
102	103	104	104	98	98	99	100	100	99	98	98	96	96	97	98	98	97	96	96
95	95	95	95	94	94	95	96	96	96	95	95	92	93	94	95	95	94	93	92
92	90	89	89	91	92	93	93	94	93	93	92	89	90	92	93	93	92	90	89
92	92	91	89	92	90	87	86	89	89	88	86	83	82	80	79	80	81	82	83
88	89	88	86	81	78	76	75	78	79	78	77	78	77	75	73	74	74	75	75
81	82	80	79	74	71	69	69	71	72	71	70	74	73	71	69	69	68	68	68
76	76	75	73	69	67	65	65	67	69	68	67	66	65	64	62	63	62	61	61
68	69	67	66	60	58	56	57	59	60	60	59	60	60	59	59	60	59	59	58
61	62	61	59	60	58	56	56	57	58	58	57	60	60	60	60	59	57	55	54
54	54	53	52	58	56	53	53	56	57	56	54	51	51	50	48	47	44	40	38
48	48	47	46	53	51    48    47    48    48    47    45    34    34    32 Figure 2. Value for Each Image Pixel										29	25	19	15	12

• 3.    Result and Discussion

Implementation of this journal is done with Matlab, where the file type used is a JPG file format. Read the image into the workspace.

RGB = imread('snatia.jpg');

Convert the image from truecolor to grayscale.

I = im2gray(RGB);

Add Gaussian noise to the image

J = imnoise(I,'gaussian',0,0.025);

Display the noisy image. Because the image is quite large, display only a portion of the image.

imshow(J(600:1000,1:600));

Remove the noise using the wiener2 function.

K = wiener2(J,[1 1]);

Display the processed image. Because the image is quite large, display only a portion of the image.

figure

imshow(K(100:300,50:400));

Image before processing

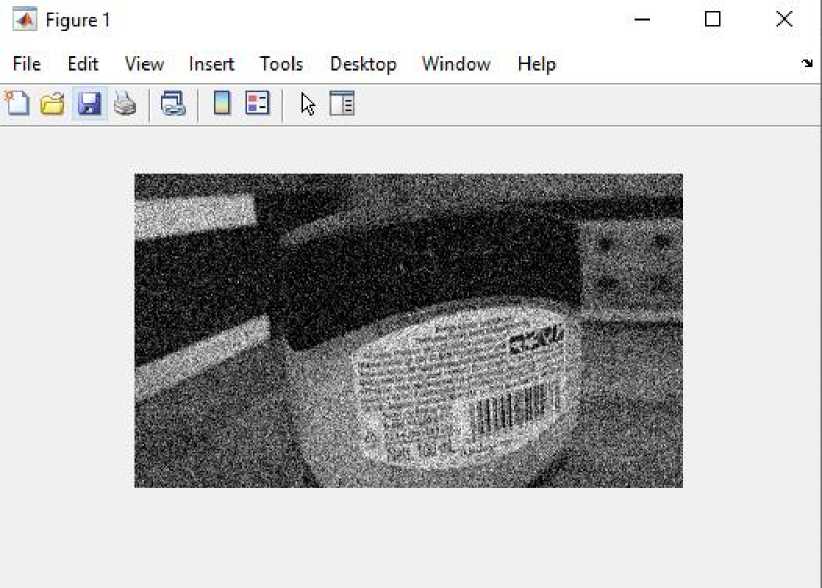
Figure 3. Before

Image after processing

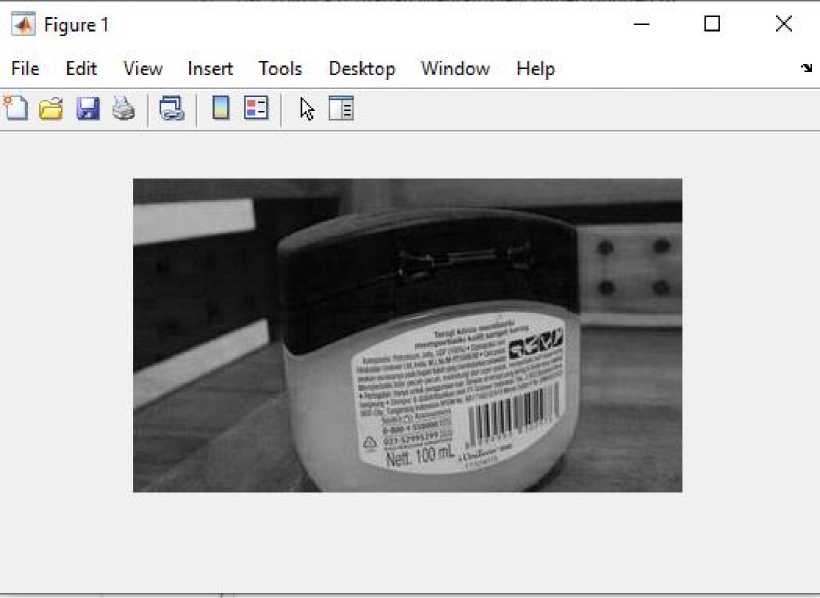
Figure 4. After

• 4.    Conclusion

It can be concluded, after doing the experiment above, it can be seen that the results of the image that initially had noise and after the image quality improvement process using Matlab showed significant results. Where, the noise in images that have undergone an image quality improvement process using Matlab seems to disappear. Seeing these results, the authors hope that further research can further develop the existing system.

References

• [1]    Simangunsong, P. B. (2018). Peningkatan Kualitas Citra Pada Studio Photography Dengan Menggunakan Metode Gaussian Filter. Jurnal Teknik Informatika Unika St. Thomas (JTIUST), 49-63.

• [2]    Sunandar, H. (2017). Perbaikan kualitas Citra Menggunakan Metode Gaussian Filter. MEANS (Media Informasi Analisa dan Sistem), 19-22.

• [3]    Syamsuddin, S. (2019). Aplikasi Peningkatan Kualitas Citra Menggunakan Metode Median Filtering Untuk Menghilangkan Noise. PROSIDING SEMINAR ILMIAH SISTEM INFORMASI DAN TEKNOLOGI INFORMASI, 227-235.

This page is intentionally left blank

58