Optimization of Artificial Neural Network Weighting in Breast Cancer Classification
on
p-ISSN: 2301-5373
e-ISSN: 2654-5101
Jurnal Elektronik Ilmu Komputer Udayana
Volume 9, No 1. August 2020
Optimasi Pembobotan Jaringan Syaraf Tiruan Pada Klasifikasi Kanker Payudara
1Kiki Dwi Prebiana, 2I Gede Santi Astawa, 3I Wayan Supriana 1,2,3Program Studi Teknik Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana
-
1,2,3Raya Kampus UNUD Bukit Jimbaran,Badung, Bali. Kode Pos: 80364. Indonesia 1kikidwiprebiana@gmail.com, 2santiastawa@gmail.com, 3iwayansupriana@gmail.com
Abstract
Klasifikasi adalah proses membedakan sekumpulan model kedalam beberapa kelas data. Salah satu algoritma yang dapat digunakan untuk proses klasifikasi adalah Jaringan Syaraf Tiruan. Salah satu proses yang memepengaruhi proses Jaringan Syaraf Tiruan adalah proses pembobotan jaringan antar neuron pada Jaringan Syaraf Tiruan. Terdapat beberapa metode yang dapat digunakan dalam proses pencarian bobot, seperti algoritma genetika dan Particle Swarm Optimization atau PSO. PSO adalah salah satu metode optimasi pada Artificle Intelegent. Pada penelitian ini akan dilakukan proses pengujian pengaruh parameter PSO terhadap hasil akurasi yang diperoleh oleh Jaringan Syaraf Tiruan. Dari penelitian yang telah dilakukan nilai parameter terbaik PSO yang digunakan adalah w=0.8, c1=1.5, dan c2 = 2.2. Dari penelitian tersebut menunjukan bahwa optimasi pebobotan dengan Particle Swarm Optimization (PSO) dapat meningkatkan rata – rata nilai akurasi sebesar 0.5%.
Keyword : Optimasi Pembobotan, Particle Swarm Optimization(PSO), Jaringan Syaraf Tiruan(JST), Parameter PSO, Akurasi
Klasifikasi merupakan proses membedakan sekumpulan model kedalam beberapa kelas data. Salah satu algortima yang kerap digunakan pada proses klasifikasi adalah Neural Network. Neural network memiliki kemampuan untuk mempelajari pola data yang dimiliki. Salah satu bagian terpenting dalam proses Jaringan Syaraf Tiruan (JST) adalah proses penentuan bobot antar jaringan pada JST. Pemberian nilai bobot pada jaringan JST merupakan salah satu hal yang banyak diteliti. Metode yang paling sering digunakan adalah metode random. Akan tetapi metode random tersebut menjadi kurang tepat dilakukan ketika data yang kita miliki adalah data denormalisasi. Sehingga diperlukan suatu optimasi pembobotan untuk menangani masalah tersebut. Terdapat beberapa metode yang dapat digunakan untuk penentuan pembobotan jaringan JST seperti metode Nguyen Widrow, Algoritma Genetika, dan Particle Swarm Optimization(PSO).
Pada penelitian sebelumnya proses optimasi pembobotan JST pada data klasifikasi kanker payudara dilakukan dengan menerapkan algoritma genetika. Pada penelitian tersebut menunjukan bahwa optimasi dengan Algoritma genetika dapat meningkatkan rata – rata akurasi, akan tetapi pada proses tersebut dibutuhkan waktu komputasi yang cukup lama (Adam Mizza Zamani, 2012). Selain itu proses optimasi pembobotan JST juga dapat menggunkan algoritma PSO, sebagai salah satu metode optimasi yang ada di Artificle Intellegent. Dari penelitian tersebut penelti bertujuan untuk mempercepat waktu kalkulasi pada proses berikutnya (training data) (SN, 2014).
Pada penelitian ini proses optimasi pembobotan jaringan pada JST akan menggunakan metode Particle Swarm Optimization(PSO). Penelitian akan berfokus pada proses pencarian
parameter terbaik PSO untuk digunakan sebagai parameter dalam proses optimasi pembobotan dengan PSO pada Jaringan Syaraf Tiruan. Hasil akurasi yang diperoleh akan dibandingkan dengan hasil akurasi dari JST yang tidak melakukan proses optimasi pembobotan.
Data yang digunakan adalah data sekunder yang diperoleh dari UCI Machine Learning Repository. Data terdiri atas 699 record data, dengan jumlah prosentase data 65.5% (458 record) kelas benign atau jinak serta 34.5% (241 record) data malignant atau ganas. Dilakukan uji korelasi pada data yang digunakan untuk mengetahui atribut yang tidak berpengaruh terhadap hasil klasifikasi. Uji korelasi dilakukan dengan menggunakan tool statistika SPSS. Uji korelasi yang dilakukan adalah korelasi bivariate. Uji korelasi bivariate digunakan untuk mengetahui hubungan antara dua buah variabel. Dari uji korelasi yang dilakukan menunjukan bahwa atribut sample code, memiliki hubungan yang lemah dengan kelas. Sehingga atribut tersebut tidak akan digunakan. Selain itu, terdapat 15 data yang satu atau lebih atributnya tidak diketahui (missing value). Pada proses preprocessing akan dilakukan proses pereduksian missing value record tersebut.
Pada penelitan ini jaringan syaraf tiruan yang digunakan terdiri atas 1 buah layer input, 1 buah hadden layer, dan 1 buah output layer. Arsitektur Jaringan Syaraf Tiruan yag digunakan ditunjukan pada gambar 1.
Gambar 1 tersebut menunjukan bahwa, input layer terdiri atas 9 buah neuron input(sesuai dengan atribut yang digunakan pada data), enam buah neuron pada hidden layer, dan satu buah neuron output. Serta terdapat bias pada input layer dan hidden layer. Arsitektur Jaringan Syaraf Tiruan adalah tetap, karena pada penelitian tidak berfokus pada pengaruh arsitektur jaringan syaraf tiruan terhadap hasil klasifikasi, melainkan pada parameter dari metode optimasi yang digunakan yaitu PSO.
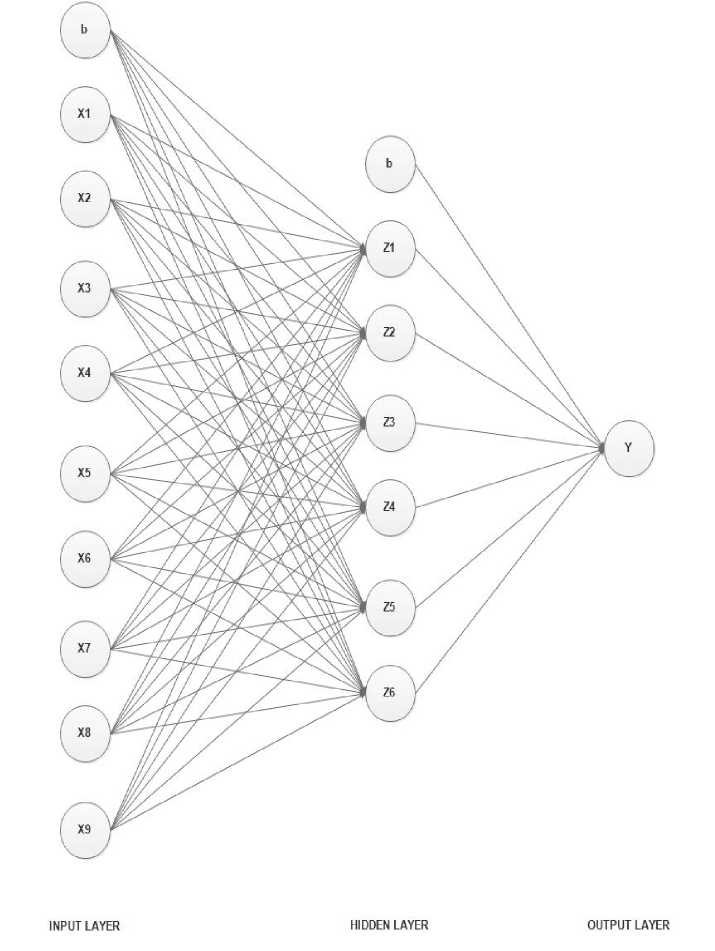
Gambar 1. Arsitektur Jaringan Syaraf Tiruan
Berikut ini adalah alur penelitian dalam optimasi pembobotan jaringan syaraf tiruan dengan menggunkan Particle Swarm Optimization (PSO).
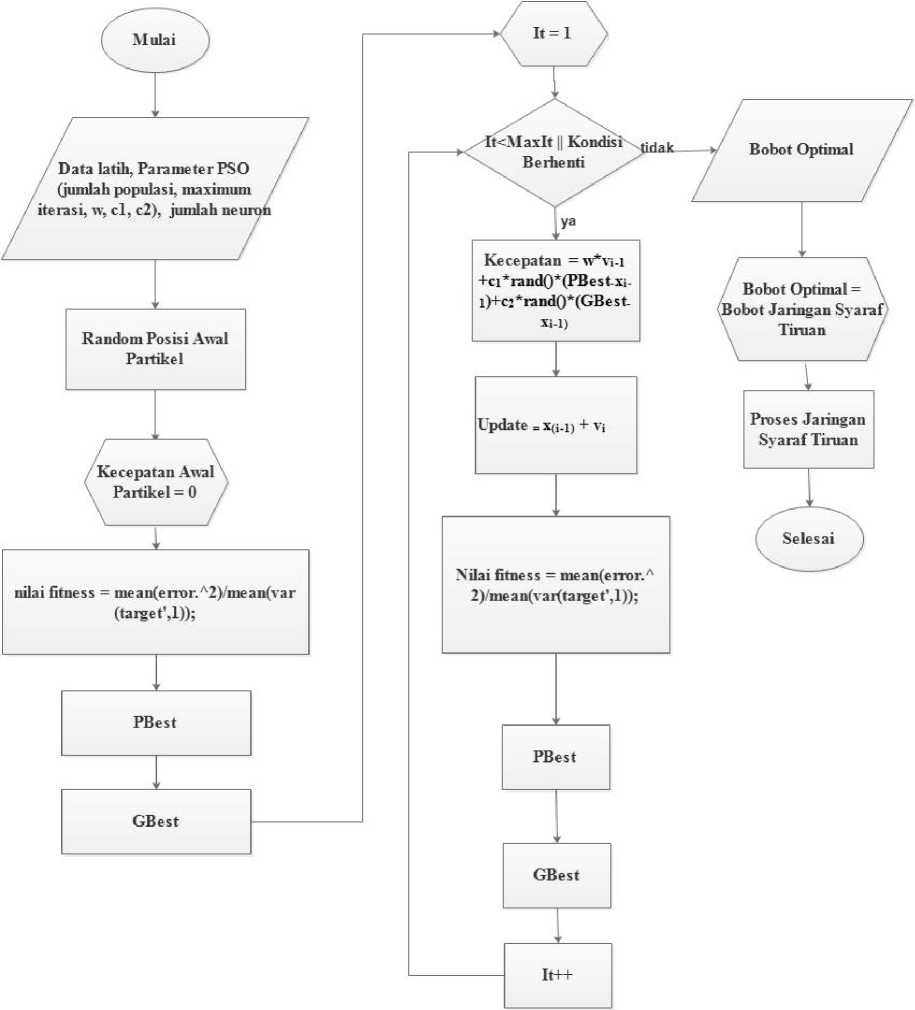
Gambar 2. diagram alir penelitian pembobotan NN dengan PSO
Gambar 2 merupakan diagram alir dari proses pembobotan dengan PSO pada Jaringan Syaraf Tiruan. Pada gambar 2 tersebut terdapat inputan berupa nilai dari parameter pso serta jumlah neuron yang dibutuhkan pada hidden layer. Dalam proses PSO akan dibangiktkan posisi awal dan kecepatan awal PSO sesuai dengan ukuran partikel yang ingin dibuat serta jumlah bobot jaringan yang dibutuhkan. Pada hasil terakhir (kondisi selesai PSO) bobot terbaik yang dihasilkan akan digunakan sebagai bobot pada jaringan syaraf tiruan. Selanjutnya akan dilakukan proses klasifikasi terhadap data uji yang ada.
Proses pengujian dilakukan terhadap 30% data yang dimiliki. Akan dilakukan proses analaisis terhadap hasil akurasi serta waktu yang dibutuhkan untuk proses train pada JST dengan menggunakan optimasi pembobotan atau tanpa optimais pembobotan. Pada proses optimasi
pembobotan akan digunakan parameter terbaik dari PSO yang telah diuji sebelumnya. Proses pencarian parameter terbaik dilakukan dengan menganalisis hasil dari masing – masing parameter yang dibangkitkan dan dipilih satu buah nilai yang paling tepat pada masng – maisng partikel. Parameter yang akan dianalisis pada penelitian ini adalah nilai w dengan rentang 0.5 sampai 1, nilai c1 antara 1.5 sampai 2, dan nilai c2 antara 2 sampai 2.5.
Perubahan pada nilai w, c1, dan c2 bertujuan untuk mendapatkan nilai parameter terbaik untuk proses optimasi pembobotan pada JST. Berikut ini adalah hasil yang diperoleh untuk pengujian yang telah dilakukan :
Berikut ini adalah hasil yang diperoleh untuk pengujian parameter w:
Tabel 1 Hasil Pengujian Parameter W
|
w=0.5 |
w=0.6 |
w=0.7 |
w=0.8 |
w=0.9 |
w=1 | |
|
Mean Iterasi |
100 |
67,4 |
42,2 |
39,8 |
28,2 |
34,6 |
|
Mean Akurasi |
98,82 |
98,14 |
97,55 |
98,73 |
95,20 |
96,08 |
Pada tabel 1 menunjukan bahwa pada pengujian parameter w, nilai w menjadi parameter independen. Dari kelima rata – rata hasil yang diperoleh menunjukan bahwa besar nilai w yang digunakan maka proses iterasi PSO yang dibutuhkan akan semakin pendek, sedangkan semakin kecil nilai w yang digunakan maka jumlah iterasi yang dibutuhkan untuk mencapai keadaan konvergen akan semakin besar. Akan tetapi hal tersebut berbanding terbalik dengan nilai akurasi yang diperoleh, semakin cepat proses PSO menunjukan rata – rata hasil akurasi yang lebih kecil dibandingkan pada proses PSO yang jumlah iterasinya cukup banyak.
Dari tabel 1 tersebut nilai w yang akan digunakan dalam optimasi pembobotan adalah w=0.8. Hal tersebut karena pada w dengan nilai 0.8 memiliki nilai akurasi yang cukup baik yaitu 98,73% dengan rata – rata iterasi yang dibutuhkan sebesar 39,8 kali.
Berikut ini adalah hasil yang diperoleh untuk pengujian parameter w:
Tabel 2 Hasil Pengujian Parameter C1
|
C1=1.5 |
C1=1.6 |
C1=1.7 |
C1=1.8 |
C1=1.9 |
C1=2 | |
|
Mean Iterasi |
25,6 |
25,2 |
26,6 |
34,6 |
27,4 |
34,6 |
|
Mean Akurasi |
95,78 |
94,61 |
94,22 |
94,61 |
95,20 |
96,08 |
Pada tabel 2 menunjukan bahwa pada pengujian parameter C1, nilai w menjadi parameter independen. Dari kelima rata – rata hasil yang diperoleh menunjukan bahwa semakin kecil nilai C1 yang digunakan menghasilkan rata – rata proses iterasi yang lebih besar dibandingkan pada C1 yang nilainya lebih kecil, akan tetapi hasil akurasi yang diperoleh tidak sebaik nilai akurasi yang diperoleh pada C1 yang nilainya lebih besar, hal tersebut dapat dilihat bahwa pada C1 dengan nilai 1.8, 1.9, dan 2 membutuhkan proses iterasi yang lebih besar dibandingkan 3 perlakuan yang lain (C1 dengan nilai 1.5 sampai 1.7). Nilai rata – rata akurasi yang diperoleh pada C1 sama dengan 2 merupakan rata – rata iterasi terbaik dibandingkan pada lima perlakuan lainnya. Akan tetapi rata – rata iterasi yang dibutuhkan meurupakan rata – rata iterasi dengan nilai tertinggi, dibandingkan pada nilai yang lain.
maka nilai C1 yang akan digunakan dalam proses optimasi pembobotan adalah C1 dengan nilai 1.5. Hal tersebut karena pada C1 dengan nilai 1.5 memiliki nilai akurasi yang cukup
baik dibandingkan pada hasil rata – rata akurasi perlakuan lainnya, selain itu jumlah rata – rata iterasi yang dibutuhkan merupakan rata – rata nilai terkecil dibandingkan pada perlakuan lainnya.
Berikut ini adalah hasil dari pengujian parameter C2 :
Tabel 3 Hasil Pengujian Parameter C2
|
C2=2 |
C2=2.1 |
C2=2.2 |
C2=2.3 |
C2=2.4 |
C2=2.5 | |
|
Mean Iterasi |
34,6 |
27,6 |
27,2 |
31,4 |
33,6 |
36,2 |
|
Mean Akurasi |
96,08 |
93,43 |
96,76 |
96,57 |
95,88 |
94,51 |
Dari tabel 3 menunjukan bahwa semakin besar nilai C2 yang digunakan, maka rata iterasi yang dibutuhkan akan semakin kecil. Begitupun dengan rata – rata akurasi yang diperoleh akan semakin kecil. Dari tabel 4.3 tersebut, maka dalam proses optimasi nilai C2 yang akan digunakan adalah 2.2, hal tersebut karena pada hasil pengujian nilai C2 sama dengan 2.2, memiliki nilai rata – rata iterasi paling baik dibandingkan pada hasil pengujian lainnya, meskipun rata – rata iterasi yang dibutuhkan bukan yang laing cepat.
Dari proses pengujian pengaruh parameter w, c1, dan c2 yang telah dilakukan maka masing – masing nilai parameter terbaik akan digunakan sebagai nilai parameter PSO dalam proses optimasi pembobotan jaringan syaraf tiruan pada klasifikasi kanker payudara. Masing – masing perlakuan (JST tanpa optimasi, JST dengan bobot optimal PSO sebagai bobot akhir, dan JST dengan bobot optimal PSO sebagai bobot awal) akan dilakukan percobaan sebanyak 10 kali percobaan. Hal ini dilakukan untuk melihat kecenderungan nilai yang diperoleh pada masing – masing perlakuan. Nilai terbaik w yang akan digunakan adalah 0.8, c1 adalah 1.6 , dan nilai dari c2 adalah 2.2. Sedangkan parameter lain dari PSO yang akan digunakan adalah 10 buah partikel, dengan maksimal iterasi sebanyak 100 iterasi. Sedangkan untuk jumlah neuron hidden yang akan digunakan adalah 6 buah neuron. Hasil pengujian optimasi pembobotan JST akan ditampilkan pada gambar berikut :
Trendline Nilai Akurasi
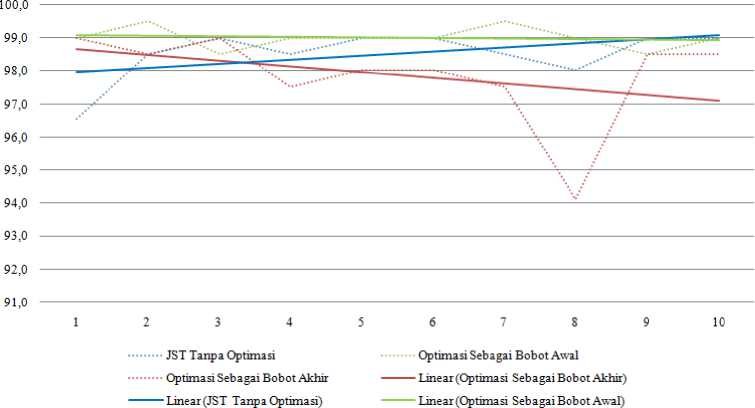
Gambar 3 Trendline Hasil Pengujian Optimasi Pembobotan
Dari gambar 3 menunjukan bahwa pada masing – masing percobaan untuk ketiga perlakuan memiliki trendline fungsi linier yang bergerak naik, dari gambar 3 menunjukan bahwa bahwa optimasi pembobotan jaringan syaraf tiruan sebagai bobot akhir memiliki trendline yang lebih rendah daripada dua perlakuan yang lain, hal tersebut juga dapat dilihat pada tabel 4.5 dimana perlakuan tersebut memiliki rata – rata akurasi yang lebih kecil yaitu 97,9 (dalam persen). Sedangkan pada kedua proses JST yang sama – sama melakukan training data, optimasi pembobotan jaringan syaraf tiruan dari sepuluh percobaan yang dilakuakan memiliki trendline yang lebih baik dibandingkan pada JST yang tidak melakukan optimasi pembobotan pada delapan percobaan pertama, sedangkan pada percobaan ke 9, trendline berada pada titik temu yang sama, dan pada percobaan ke 10, trendline pada JST yang tidak melakukan proses optimasi lebih baik dari pada trendline yang dimilki oleh JST yang melakukan proses optimasi pembobotan. Pada JST dengan melakukan proses optimasi pembobotan memiliki rentang hasil diantara nilai 98.5 – 99.5 (dalam persen), sedangkan pada JST yang tidak melakukan proses optimasi berada pada rentang nilai 96.6 – 99.00 (dalam persen). Selain nilai akurasi berikut ini adalah traindline yang menyajikan waktu tarin yang dibuthkan oleh Jaringan Syaraf Tiruan ketika melakukan optimasi pembobotan dan tanpa melakukan optimasi pembobotan :
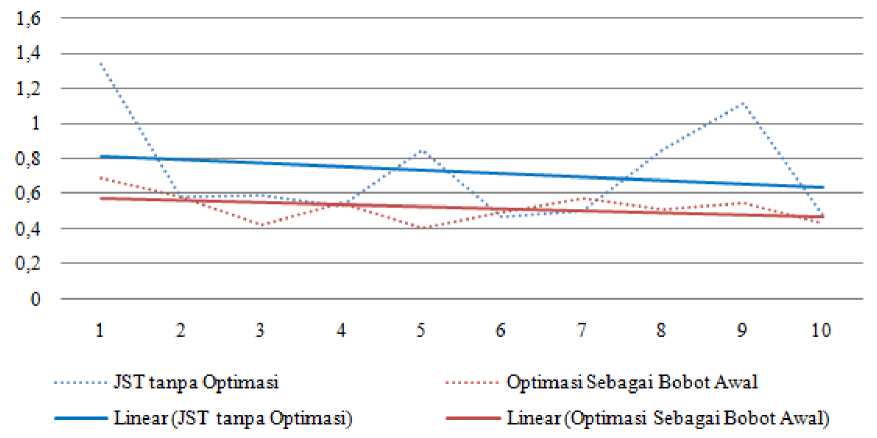
Gambar 4 Traindline Waktu Train
Dari gambar 4 menunjukan bahwa traindline waktu train yang dibutuhkan oleh JST yang tidak melakukan proses optimasi selalu lebih tinggi dibandingkan oleh waktu train yang dibutuhkan pada JST yang sebelumnya melakukan proses optimasi pembobotan. Proses JST membutuhkan waktu train antara 0.46639 – 1.335638 sedangkan pada JST yang melakukan optimasi pembobotan waktu train yang dibutuhkan berada ada rentang nilai antara 0,40561 -0.687815.
Dari penelitian yang telah dilakukan dapat diimpulkan bahwa parameter terbaik Partcle Swarm Optimization (PSO) yang digunakan adalah nilai w = 0.8, C1=1.5, dan C2 = 2.2. Dari proses pengujian yang dilakukan menunjukan bahwa optimasi pembobotan JST memiliki rata – rata akurasi yaitu 0.5 % lebih baik dibandingkan rata – rata JST yang tidak melakukan proses optimasi pembobotan. Sedangkan pada waktu yang dibutuhkan untuk proses train, proses optimasi pembobotan memiliki rata – rata waktu train yang lebih kecil dibandingkan waktu train JST tanpa proses optimasi pembobotan.
Saran yang dapat diberikan untuk penelitian lebih lanjut dalam melakukan klasifikasi kanker payudara dapat dilakukan dengan mengetahui parameter PSO yang lain seperti jumlah partikel yang digunakan, serta maximum iterasi yang dibutuhkan pada proses pencarian bobot optimal.
Abraham Ishak Bekalani, Y. A. (2013). Prediksi Tinggi Signifikansi Gelombang Laut di Bagian Wilayah Perairan Indonesia Menggunakan Jaringan Syaraf Tiruan Metode Propagasi Balik. Prima Fisika , 40-49.
Adam Mizza Zamani, B. A. (2012). Implementasi Algoritma Genetika pada Struktur
Backpropagation Neural Network untuk Klasifikasi Kanker Payudara. Jurnal Teknik ITS , 1-6.
Arif Jurnarwanto, R. H. (2009). Aplikasi Jaringan Syaraf Tiruan Backpropagation Untuk Memprediksi Penyakit Hati di Rumah Sakit Mardi Rahayu Kudus. Jurnal Teknik Elektro , 11-21.
Azhari, H. G. (2014). Pelatihan Bobot Jaringan Syaraf Tiruan Menggunakaan PArticle Swarm Optimization Untuk Peramalan Tingkat Inflasi. Berkala MIPA , 292-302.
Dongshu Wang, D. T. (2018). Particle Swarm Optimization algorithm : an overview. Soft Comput , 387-408.
Lubis, M. R. (2017). Meode Hybrid Particle Swarm Optimization - Neural Network Backpropagation untuk Prediksi Hhasil Pertandingan Sepak Bola. Jurnal Sains Komputer & Informatika (j-SAKTI) , 1-13.
Lubis, M. R. (2017). Metode Hybrid Particle Swarm Optimization- Neural Network Backpropagation Untuk Prediksi HAsil Pertandingan Sepak Bola. Jurnal Sains Komputer & Informatika (J-SAKTI) , 72-83.
Maickel Tuegeh, A. S. (2009). Optimal Generator Scheduling Based On Particle Swarm
Optimization. Seminar Nasional Informatika 2009 , 25-32.
Miftah Rahmalia Ariyati, A. R. (2018). Autonomous Robot Path Planning Menggunakan Perbandingan Metode Particle Swarm Optimization dan Genetic Algorithm. Jurnal Buana Informatika , 61-70.
N.K, B. M. (2015). Predicting Cummulative Number of Failures in Softwere Using an ANN-PSO Based Approach. IEEE , 9-14.
Rani, L. N. (2015). Klasifikasi Nasabah Menggunakan Algoritma C4.5 Sebagai Dasar Pemberian Kredit. Jurnal KomTekInfo fakultas Ilmu Komputer , 33-38.
Ridla, M. A. (2018). Particle Swarm OPtimization sebagai penentu nilai bobot pada Artificial Neural Network Berbasis Backpropagation Untuk Prediksi Tingkat Penjualan Minyak Pelumas Pertamina. Jurnal Ilmiah Informatika , 183-192.
Rusell C. Eberhart, Y. S. (2001). Particle Swarm Optimization : Develompment, APplications and Resources. IEEE , 81-86.
SN, H. G. (2014). Optimasi Bobot Jaringan Syaraf Tiruan Menggunakan Particle Swarm Optimization. IJCCS , 25-36.
159
Discussion and feedback