Pengaruh Membership Function pada Fuzzy Dempster- Shafer
on
p-ISSN: 2301-5373
e-ISSN: 2654-5101
Jurnal Elektronik Ilmu Komputer Udayana
Volume 9, No 1. August 2020
Pengaruh Membership Function pada Fuzzy Dempster-Shafer
Frisca Olivia Goriantoa1, I Gede Santi Astawaa2, I Gusti Agung Gede Arya Kadyanana3
aProgram Studi Teknik Informatika, Universitas Udayana
Bali, Indonesia 1fgorianto@gmail.com 2santiastawa@gmail.com 3gungde@unud.ac.id
Abstract
Pada proses klasifikasi selalu akan muncul ketidakpastian. Ketidakpastian berupa kemungkinan bahwa label kelas yang dipilih tidak tepat sehingga menyebabkan keraguan. Salah satu metode untuk menangani hal ini adalah menggunakan metode Fuzzy dan Dempster – Shafer (DS). Penelitian ini akan mengkombinasikan tahap Fuzzification dari metode Fuzzy untuk mendapatkan nilai Belief yang kemudian akan digunakan pada perhitungan klasifikasi DS. Penelitian ini bertujuan untuk mengetahui pengaruh dari penggunaan Membership Function (MF) yang berbeda – beda dalam proses klasifikasi serta parameter optimal masing-masing MF yang digunakan. Dari penelitian yang telah dilakukan didapatkan hasil bahwa parameter yang optimal bagi bentuk MF segitiga adalah a1 = a2 = 4, b1 = b2 = 10, c1 = 0 dan c2 = 11 dan bentuk MF bell adalah a1 = -11, b1 = 0, c1 = 11 dan a2 = 0, b2 = 1, c2 = 22. 2. Hasil penelitian menunjukkan bahwa bentuk MF bell dengan akurasi 88,87% lebih baik daripada MF segitiga.
Keywords: Fuzzification, Dempster – Shafer, Parameter, Membership Function
Proses klasifikasi adalah proses pemberian label kelas terhadap sekumpulan data yang belum memiliki label kelas [1]. Label kelas akan ditentukan dengan memilih label kelas yang memiliki probabilitas terbesar. Pada proses klasifikasi selalu akan muncul ketidakpastian. Ketidakpastian berupa kemungkinan bahwa label kelas yang dipilih tidak tepat sehingga menyebabkan keraguan. Salah satu metode yang dapat digunakan untuk mengatasi ketidakpastian dalam klasifikasi adalah menggunakan metode Fuzzy dan Dempster – Shafer (DS).
Metode ini dapat menghitung probabilitas suatu label kelas berdasarkan data yang diinputkan dan menetapkan label kelas berdasarkan nilai probabilitas yang paling besar. Penelitian ini akan mengkombinasikan tahap Fuzzification dari metode Fuzzy untuk mendapatkan nilai Belief yang kemudian akan digunakan pada perhitungan klasifikasi DS. Kelebihan dari menggunakan ini adalah tidak perlu mencari pakar untuk mendapatkan nilai Belief yang akan digunakan pada DS.
Tahap Fuzzification menggunakan Membership Function (MF) untuk menghasilkan nilai kepercayaan atau nilai Belief terhadap kelas. MF sendiri memiliki banyak bentuk yang berbeda-beda [2] sehingga muncul pertanyaan bentuk MF manakah yang lebih optimal dalam melakukan proses klasifikasi. Beberapa penelitian sebelumnya juga sudah melakukan perbandingan menggunakan bentuk – bentuk MF yang berbeda. Salah satunya adalah penelitian mendiagnosis penyakit tanaman cabai dengan menggunakan metode Fuzzy dan Dempster – Shafer. Penelitian ini menggunakan proses Fuzzification untuk mencari nilai Belief berdasarkan tingkatan kerusakan gejala yang dipilih. Nilai Belief tersebut digunakan pada perhitungan Dempster – Shafer dalam menghasilkan persentase besarnya kemungkinan penyakit tersebut menyerang tanaman cabai. MF atau Fungsi Keanggotaan yang digunakan pada penelitian ini adalah kombinasi bentuk fungsi linear dan fungsi segitiga [3].
Penelitian selanjutnya adalah evaluasi bentuk MF pada induksi motor drive yang dikontrol menggunakan Fuzzy. Penelitian ini melakukan evaluasi sensitivitas dan perbandingan antar bentuk-bentuk MF yang berbeda. Bentuk MF yang dibandingkan adalah bentuk segitiga, gaussian, bell, sigmoid, dan trapesium. Penelitian ini menunjukkan bahwa bentuk MF segitiga
menghasilkan performa yang lebih baik daripada bentuk MF lainnya [4]. Penelitian selanjutnya yang dilakukan oleh Mashaly adalah melakukan perbandingan bentuk MF non-linear (bell, gaussian, dan sigmoid) untuk mengoptimasi Adaptive Neuro-Fuzzy Inference System (ANFIS) dalam memodelkan produktivitas tenaga surya. Hasil penelitiannya menunjukkan bahwa menggunakan bentuk MF bell menghasilkan performa yang paling baik dan menghasilkan nilai eror yang paling kecil [5].
Metode Fuzzy Dempster – Shafer akan diuji untuk melakukan klasifikasi menggunakan data kanker payudara Wisconsin Breast Cancer Data (WBCD) yang didapatkan dari UCI Machine Learning Repository. Penelitian ini akan melakukan perbandingan bentuk MF bell dan segitiga untuk menghasilkan nilai Belief masing – masing gejala. Nilai Belief tersebut digunakan dalam perhitungan kombinasi DS untuk mendapatkan nilai kemungkinan suatu kejadian atau penyakit berdasarkan data yang digunakan.
Penelitian ini berjudul “Pengaruh Membership Function pada Fuzzy Dempster – Shafer” dengan tujuan untuk mengetahui pengaruh dari penggunaan Membership Function (MF) yang berbeda – beda dalam proses klasifikasi. Penelitian ini melakukan proses klasifikasi yang secara garis besar membandingkan hasil klasifikasi Fuzzy Dempster – Shafer ketika menggunakan bentuk MF segitiga dan ketika menggunakan bentuk MF bell.
Proses klasifikasi dalam penelitian ini dibagi menjadi dua tahap utama, yaitu tahapan Fuzzification dan tahapan perhitungan Dempster – Shafer (DS). Pada tahap Fuzzification, hal pertama yang dilakukan adalah menentukan parameter yang digunakan. Hal selanjutnya adalah sistem akan melakukan perhitungan nilai Belief yang didapatkan dari nilai hasil rumus MF atau fungsi keanggotaan Fuzzy dengan bentuk dan parameter yang sudah ditentukan sebelumnya. Bentuk MF yang digunakan adalah bentuk segitiga dan bell. Nilai Belief yang dihasilkan memiliki rentang 0 sampai 1 di mana nilai 0 memiliki arti kemungkinan kelas tersebut tidak ada atau tidak mungkin sedangkan nilai 1 memiliki arti sudah pasti kelas tersebut dan tidak ada keraguan atau ketidakpastian.
Percobaan parameter kurva MF yang digunakan dibagi menjadi dua bagian, yaitu bagian pertama adalah di mana parameter titik pusat kurva berada di dalam rentang data input dan kedua adalah menggunakan parameter titik pusta kurva yang berada di luar rentang data input. Hal ini dilakukan karena dengan menggunakan parameter yang berada di dalam rentang data input dapat menghasilkan nilai Belief = 1 sedangkan proses klasifikasi selalu memiliki ketidakpastian [6]. Oleh karena itu, dilakukan bagian kedua, yaitu menggunakan parameter titik pusat kurva yang berada di luar rentang data input sehingga dalam tahap Fuzzification menghasilkan nilai Belief yang tidak bernilai 1 untuk merepresentasikan data yang memiliki ketidakpastian. Nilai – nilai parameter yang digunakan dalam kurva MF dibentuk sedemikian rupa sehingga menghasilkan kurva MF bentuk segitiga dan bell yang simetris [7]. Jika parameter dan bentuk kurva MF sudah ditetapkan dan menghasilkan nilai Belief, selanjutnya masuk ke tahap perhitungan Dempster – Shafer.
Tahapan Dempster – Shafer akan menerima nilai Belief yang didapatkan dari tahap Fuzzification kemudian melakukan perhitungan nilai kemungkinan setiap kelas dengan cara menghitung nilai densitas (m) atau nilai keyakinan menggunakan Dempster’s Rule of Combination (DRC). DRC akan menghasilkan nilai densitas masing – masing kelas. Nilai densitas masing – masing kelas inilah yang digunakan sebagai nilai keyakinan sehingga proses klasifikasi dilakukan dengan memilih kelas dengan nilai densitas terbesar.
Penelitian ini berhubungan dengan melakukan diagnosis suatu kelainan atau penyakit berdasarkan gejala yang ada sehingga data yang digunakan adalah Wisconsin Breast Cancer Data (WBCD). Data tersebut berupa data sekunder yang didapatkan dari UCI Machine Learning Repository [8] berisikan data – data pengukuran menentukan tumor malignant (tumor abnormal) atau tumor benign (tumor normal).
Tabel 1. Atribut dan Nilai Korelasinya
|
No |
Atribut Data |
Nilai Atribut |
|
1 |
Sample code number |
Nomor ID |
|
2 |
Clump Thickness |
1 - 10 |
|
3 |
Uniformity of Cell Size |
1 - 10 |
|
4 |
Uniformity of Cell Shape |
1 - 10 |
|
5 |
Marginal Adhesion |
1 - 10 |
|
6 |
Single Epithelial Cell Size |
1 - 10 |
|
7 |
Bare Nuclei |
1 - 10 |
|
8 |
Bland Chromatin |
1 - 10 |
|
9 |
Normal Nucleoli |
1 - 10 |
|
10 |
Mitoses |
1 - 10 |
|
11 |
Class |
2 untuk normal dan 4 untuk abnormal |
Data ini memiliki 11 atribut yang memiliki nilai dengan rentang 1 sampai 10 (kecuali atribut Sample code number dan class) dan atribut Class yang memiliki dua nilai, yaitu kelas malignant (abnormal) direpresentasikan dengan nilai 4 dan kelas benign (normal) direpresentasikan dengan nilai 2. Data ini memiliki 699 data item, dengan 241 item adalah data kelas abnormal dan 458 item data kelas normal.
-
2.3. Parameter Membership Function
Bentuk MF yang digunakan akan dibuat berdasarkan analisis atribut data sebelumnya. Dua bentuk MF yang digunakan adalah segitiga dan bell, dimana masing-masing MF memiliki 3 parameter. Keterangan parameter yang digunakan dalam masing – masing bentuk dapat dilihat pada Tabel 2. Bentuk MF segitiga memiliki parameter a adalah titik mulai, b adalah titik pusat kurva, dan c adalah titik akhir kurva. Bentuk bell memiliki parameter a adalah lebar kurva, b tingkat kemiringan kurva, dan c titik pusat kurva. Dalam penelitian ini akan dilakukan proses klasifikasi menggunakan bentuk MF serta parameter yang berbeda – beda. Nilai – nilai parameter yang digunakan dalam kurva MF dibentuk sedemikian rupa sehingga menghasilkan kurva MF bentuk segitiga dan bell yang simetris [7].
Tabel 2. Parameter Bell dan Segitiga
|
No. |
Parameter |
Bentuk MF Segitiga |
Bentuk MF Bell |
|
1 |
a |
Titik mulai kurva |
Lebar kurva |
|
2 |
b |
Titik pusat kurva |
Tingkat kemiringan kurva |
|
3 |
c |
Titik akhir kurva |
Titik pusat kurva |
Pada Gambar 1, kurva segitiga pertama memiliki tiga parameter a1, b1, dan c1. Pada gambar tersebut parameter a1 tidak terlihat karena berada diluar rentang data yang digunakan. Sedangkan pada kurva segitiga kedua memiliki parameter a2, b2, dan c2. Pada kurva kedua ini parameter c2 tidak terlihat karena berada diluar rentang data. Seperti pada gambar diatas, kurva bell memiliki tiga parameter akan tetapi hanya parameter c1 dan c2 yang menunjukkan titik pusat kurva karena parameter lainnya menunjukkan lebar dan tingkat kemiringan. Bentuk MF segitiga dan bell dibuat simetris dan ukuran yang sama. Penggunaan perbedaan parameter yang digunakan dalam kurva Membership Function (MF) dibagi menjadi dua bagian. Bagian pertama adalah dengan menggunakan titik pusat kurva yang berada di dalam rentang data. Bagian kedua adalah dengan menggunakan titik pusat kurva yang berada diluar rentang data. Rentang data yang dimaksud adalah rentang nilai atribut data WBCD dengan nilai antara 1 sampai 10 dan
memiliki karakteristik data dimana semakin kecil nilai cenderung menunjukkan kelas normal sedangkan semakin besar nilai cenderung menunjukkan kelas abnormal.
Bagian pertama adalah dimana bentuk MF segitiga dan bell menggunakan titik pusat kurva kelas normal dan kelas abnormal yang berada di dalam rentang data, dalam hal ini berarti titik pusat kelas normal = 1 dan berarti titik pusat kelas abnormal = 10. Akan tetapi penggunaan parameter dalam rentang data ini dapat menghasilkan nilai Belief = 1 yang artinya tidak ada keraguan atau ketidapastian. Oleh karena itu dilakukan bagian kedua, atau penggunaan parameter titik pusat kurva diluar rentang data. Pada bagian kedua dilakukan dua kali percobaan, yaitu dengan menggunakan parameter titik pusat kurva kelas normal = 0 serta titik pusat kurva kelas abnormal = 11 dan menggunakan parameter titik pusat kurva kelas normal = -1 serta titik pusat kurva kelas abnormal = 12. Nilai titik pusat kurva untuk kedua kelas terjadi perubahan yang sama, yaitu jika titik pusat kurva kelas normal berpindah dari 0 ke -1 maka titik pusat kurva abnormal juga akan berpindah satu kali dari 11 ke 12. Hal ini dilakukan agar bentuk masing – masing kurva tetap simetris [7].
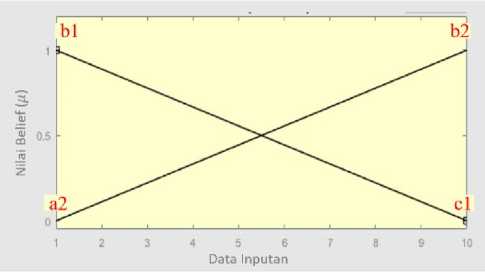
Gambar 1. Bentuk MF Segitiga
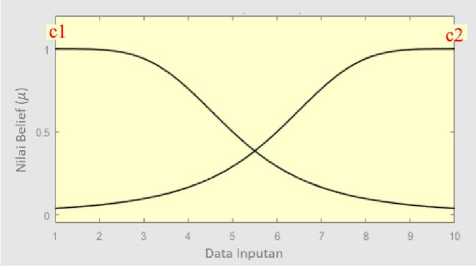
Gambar 2. Bentuk MF Bell
Gambar 3 adalah diagram alir sistem dalam melakukan proses klasifikasi. Sistem dimulai dengan membaca data WBCD lalu menetapkan beberapa variabel. Variabel baris menyimpan jumlah baris yang ada di dalam data WBCD, dalam penelitian ini jumlah baris data yang digunakan adalah 683 sesuai dengan jumlah data item setelah dilakukan pengolahan data sebelumnya.
Variabel baris_ke berfungsi sebagai counter dalam perhitungan iterasi setiap baris data. Sedangkan maxite adalah jumlah iterasi yang harus dilakukan Dempster – Shafer’s Rule of Combination (DRC) dan ite adalah sebagai counter perhitungan iterasi maxite. Lalu dilakukan pemilihan bentuk MF yang diinginkan dan parameternya seperti yang sudah ditentukan. Setelah itu sistem masuk ke bagian proses klasifikasi pada baris data pertama yang dimulai dengan tahap fuzzifikasi. Sistem akan menghitung nilai Belief setiap gejala yang ada di baris data pertama menggunakan rumus fungsi keanggotaan yang sesuai dengan bentuk MF yang dipilih. Gejala yang dimaksud disini adalah atribut data, data WBCD memiliki 9 atribut sehingga pada tahap ini sistem akan melakukan perhitungan nilai Belief untuk kesembilan atribut.
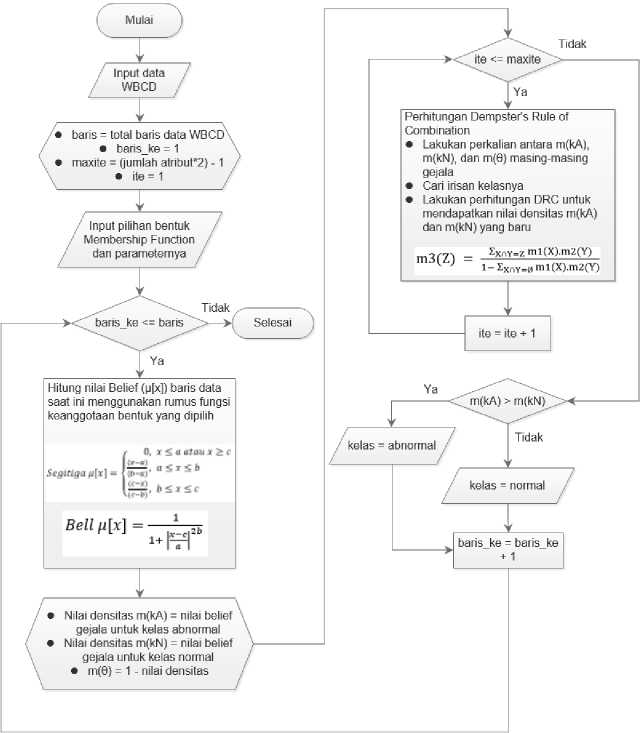
Gambar 3. Diagram Alir
Setiap satu gejala akan menghasilkan dua nilai Belief, yaitu nilai Belief untuk kelas normal dan abnormal. Setelah mendapatkan nilai Belief, tetapkan nilai – nilai tersebut sebagai nilai densitas sesuai kelasnya masing – masing. Dengan m(kA) adalah nilai densitas kelas abnormal, m(kN) adalah nilai densitas kelas normal, dan hitung juga nilai plausibility masing – masing kelas.
Langkah selanjutnya adalah memulai iterasi menghitung nilai keyakinan menggunakan Dempster’s Rule of Combination (DRC). Proses perhitungan DRC dilakukan untuk setiap nilai densitas masing – masing gejala. Nilai densitas masing – masing kelas tersebut akan terus diperbarui sampai iterasi selesai. Setelah iterasi selesai, dilakukan pengujian jika nilai densitas m(kA) lebih besar dari m(kN) maka data dengan gejala – gejala yang sudah dihitung tadi termasuk ke dalam kelas abnormal, jika tidak maka termasuk ke dalam kelas normal. Klasifikasi pada baris pertama data selesai, nilai baris_ke bertambah dan sistem memulai proses klasifikasi ke baris data selanjutnya. Semua proses ini dilakukan terus sampai ke baris data terakhir.
Berdasarkan [9], pengertian Fuzzy secara Bahasa adalah kabur atau samar-samar. Logika Fuzzy merupakan suatu logika yang memiliki nilai kekaburan atau kesamaran (fuzzyness) antara benar atau salah. Namun berapa besar keberadaan dan kesalahan suatu tergantung pada bobot keanggotaan yang dimilikinya. Logika fuzzy digunakan untuk menterjemahkan suatu besaran yang diekspresikan menggunakan bahasa(linguistik), misalkan besaran kecepatan laju kendaraan yang diekspresikan dengan pelan, agak cepat, cepat, dan sangat cepat. Logika Fuzzy pertama kali dikenalkan oleh [10] dimana integrasi logika fuzzy ke dalam sistem dapat membuat keputusan sendiri dan terkesan seperti memiliki perasaan, karena memiliki keputusan lain selain iya (logika 1) dan tidak (logika 0). Membership Function (MF) atau fungsi keanggotaan adalah suatu kurva yang menunjukkan pemetaan titik-titik input data ke dalam nilai keanggotaannya
(derajat keanggotaan) yang memiliki interval antara 0 sampai 1 [11]. MF sendiri memiliki banyak jenis yang dapat digunakan [12]:
-
1. Fungsi Segitiga
Kurva segitiga pada dasarnya merupakan gabungan antara 2 garis, yaitu linear naik dan
linear turun. Bentuk ini memiliki 3 parameter, yaitu a sebagai titik mulai, c sebagai
titik akhir, dan b sebagai titik tengah kurva dan memiliki fungsi keanggotaan:
-
r 0, x ≤
(x-a) _
, a ≤ μ[x] = < (b-a),
∖ (⅛ b≤
V(c-b)'
a atau x≥ c
x ≤ b
x ≤ c
(1)
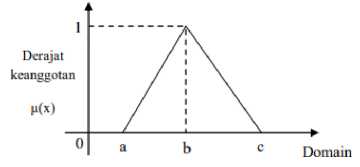
Gambar 4. Fungsi Segitiga
-
2. Fungsi Bell
Karena kelancaran dan notasi singkatnya, MF Bell menjadi semakin populer untuk menentukan set fuzzy. Bentuk MF ini memiliki bentuk simetris dan ditentukan oleh tiga parameter (a, b, c) di mana b parameter kemiringan kurva, parameter c menempatkan pusat kurva dan a menunjukkan lebar kurva. Fungsi keanggotaan bell:
1
f(χ; a,b, c) = 2t (2)
1+ l^-"1
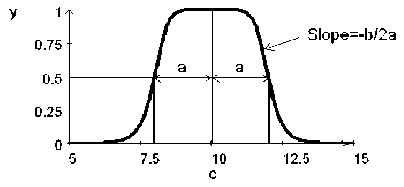
Gambar 5. Fungsi Bell
Teori Dempster-Shafer (DS) adalah suatu teori matematika untuk pembuktian berdasarkan Belief functions (fungsi kepercayaan) dan plausible reasoning (pemikiran yang masuk akal), yang digunakan untuk mengkombinasikan potongan informasi yang terpisah (bukti) untuk mengkalkulasi kemungkinan dari suatu peristiwa [13]. Dempster-Shafer akan digunakan untuk menghitung keyakinan apakah dari gejala-gejala (atribut) yang dialami, tumor tersebut termasuk tumor ganas (malignant) atau jinak (benign).
Secara umum teori Dempster-Shafer ditulis dalam suatu interval [Belief, Plausibility]. Belief (Bel) adalah ukuran kekuatan evidence dalam mendukung suatu himpunan proposisi. Jika bernilai 0 maka mengindikasikan bahwa tidak ada evidence, dan jika bernilai 1 menunjukkan adanya kepastian. Dan plausibility (Pl) dinotasikan sebagai:
Pl(x) = 1- Bel(x) (3)
Pada teori Dempster-Shafer dikenal adanya frame of discernment atau semesta pembicaraan dari sekumpulan hipotesis yang dinotasikan dengan θ. Sedangkan mass function atau bisa disebut juga probabilitas mass value atau fungsi densitas (m) dalam teori Dempster-
Shafer adalah tingkat kepercayaan dari suatu bukti. Nilai m(A) adalah ukuran probabilitas dari bukti – bukti yang mendukung hipotesis A. Untuk mengatasi sejumlah evidence pada teori DS menggunakan aturan yang lebih dikenal dengan Dempster’s Rule of Combination (DRC). Jika diketahui X adalah subset dari Θ dengan m1 sebagai fungsi densitasnya, dan Y juga subset dari Θ dengan m2 sebagai fungsi densitasnya maka dapat dibentuk fungsi kombinasi DRC m1 dan
m2 sebagai m3 dengan persamaan:
ΣX∩Y=Z m1(X).m2(Y)
1- ΣX∩Y=Ø m1(X).m2(Y)
(4)
m3(Z) =
m1 (X) = nilai densitas dari evidenceX
m2 (Y) = nilai densitas dari evidenceY
m3 (Z) = nilai densitas dari evidenceZ
m3(Z) adalah nilai densitas terbaru dari hasil kombinasi dua nilai densitas pertama. Caranya adalah dengan mengkalikan nilai densitas yang memiliki hipotesis yang beririsan. Lalu dibagi oleh hasil pengurangan 1 dan nilai densitas yang tidak memiliki irisan hipotesis.
Proses penentuan parameter-parameter yang digunakan dalam penelitian ini dibagi menjadi dua bagian utama, yaitu bagian pertama menggunakan nilai titik pusat kurva dalam rentang data dan bagian kedua diluar rentang data. Setiap satu grafik MF terdapat dua kurva yang merepresentasikan dua kelas data, yaitu kelas normal dan kelas abnormal. Sehingga setiap satu grafik MF memiliki dua kurva juga, yaitu kurva kelas normal dan kelas abnormal.
Bentuk MF segitiga memiliki parameter a adalah titik mulai, b adalah titik pusat kurva, dan c adalah titik akhir kurva. Pada penelitian bagian pertama ini, digunakan parameter titik pusat kurva kelas normal (b1) dan kelas abnormal (b2) yang termasuk dalam rentang data, yaitu b1 = 1 dan b2 = 10. Parameter a1, b1, dan c1 adalah parameter kurva pertama, yaitu kurva kelas normal. Sedangkan parameter a2, b2, c2 adalah parameter kurva kedua, yaitu kelas abnormal. Pada penelitan bagian pertama ini parameter b1 dan b2 sebagai titik pusat tidak berubah atau tetap menggunakan nilai b1 = 1 dan b2 = 10.
Tabel 3. Parameter MF Segitiga dalam Rentang Data
|
Percobaan ke- |
Nilai Parameter yang Digunakan | |||||
|
a1 |
b1 |
c1 |
a2 |
b2 |
c2 | |
|
1 |
-8 |
1 |
10 |
1 |
10 |
19 |
|
2 |
-7 |
1 |
9 |
2 |
10 |
18 |
|
3 |
-6 |
1 |
8 |
3 |
10 |
17 |
|
4 |
-5 |
1 |
7 |
4 |
10 |
16 |
|
5 |
-4 |
1 |
6 |
5 |
10 |
15 |
Parameter c1 dan a2 akan mengalami pergeseran nilai, hal ini dikarenakan kedua parameter tersebut mempengaruhi panjang lebar garis kurva di dalam rentang data inputan yang secara langsung juga mempengaruhi nilai Belief dalam tahap fuzzifikasi. Sedangkan parameter a1 dan c2 tidak berpengaruh karena berada diluar rentangan data inputan.
Selanjutnya adalah menentukan parameter MF bentuk bell. Bentuk bell memiliki parameter a adalah lebar kurva, b tingkat kemiringan kurva, dan c titik pusat kurva. Parameter titik pusat MF bell berada di dalam rentang nilai data inputan, yaitu c1 =1 untuk titik pusat kurva kelas normal dan c2 = 10 untuk titik pusat kurva kelas abnormal. Pada bentuk bell ini parameter yang berubah adalah parameter lebar kurva (a) dan tingkat kemiringan kurva (b). Dimana untuk satu nilai parameter a1 dan a2 akan diuji dengan sepuluh parameter b1 dan b2 yang berbeda
seperti pada Tabel 4.2. Nilai parameter a1 = a2 serta nilai b1 = b2 untuk setiap percobaan agar bentuk MF bell tetap simetris.
Tabel 4. Parameter MF Bell dalam Rentang Data
|
Percobaan ke- |
Nilai Parameter yang Digunakan | |||||
|
a1 |
b1 |
c1 |
a2 |
b2 |
c2 | |
|
1 |
1 |
1 |
1 |
1 |
1 |
10 |
|
2 |
1 |
2 |
1 |
1 |
2 |
10 |
|
3 |
1 |
3 |
1 |
1 |
3 |
10 |
|
. . dst. |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
70 |
7 |
10 |
1 |
7 |
10 |
10 |
Total percobaan yang dilakukan adalah 70 percobaan dengan perubahan nilai parameter a dari 1 sampai 7, parameter b dari 1 sampai 10, sedangkan parameter c1 dan c2 tidak berubah. Parameter a dilakukan percobaan sampai 7 karena semakin besar nilai a maka kurva bell akan semakin lebar sampai menutupi daerah data inputan seperti garis lurus.
Pada bagian ini dilakukan dua kali percobaan, yaitu yang pertama menggunakan titik pusat kurva 0 untuk kelas normal dan 11 untuk kelas abnormal, dan yang kedua adalah menggunakan titik pusat kurva -1 untuk kelas normal dan 12 untuk kelas abnormal.
Bentuk MF segitiga memiliki parameter a adalah titik mulai, b adalah titik pusat kurva, dan c adalah titik akhir kurva. Setiap bentuk MF akan dilakukan dua kali percobaan menggunakan titik pusat kurva yang berbeda.
Tabel 5. Parameter MF Segitiga Titik Pusat 0 dan 11
|
Percobaan ke- |
Nilai Parameter yang Digunakan | |||||
|
a1 |
b1 |
c1 |
a2 |
b2 |
c2 | |
|
1 |
-11 |
0 |
11 |
0 |
11 |
22 |
|
2 |
-10 |
0 |
10 |
1 |
11 |
21 |
|
3 |
-9 |
0 |
9 |
2 |
11 |
20 |
|
4 |
-8 |
0 |
8 |
3 |
11 |
19 |
|
5 |
-7 |
0 |
7 |
4 |
11 |
18 |
|
6 |
-6 |
0 |
6 |
5 |
11 |
17 |
Tabel 6. Parameter MF Segitiga Titik Pusat -1 dan 12
|
Percobaan ke- |
Nilai Parameter yang Digunakan | |||||
|
a1 |
b1 |
c1 |
a2 |
b2 |
c2 | |
|
1 |
-14 |
-1 |
12 |
-1 |
12 |
25 |
|
2 |
-13 |
-1 |
11 |
0 |
12 |
24 |
|
3 |
-12 |
-1 |
10 |
1 |
12 |
23 |
|
4 |
-11 |
-1 |
9 |
2 |
12 |
22 |
|
5 |
-10 |
-1 |
8 |
3 |
12 |
21 |
|
6 |
-9 |
-1 |
7 |
4 |
12 |
20 |
|
7 |
-8 |
-1 |
6 |
5 |
12 |
19 |
Parameter b1 dan b2 sebagai titik pusat tidak berubah atau tetap menggunakan nilai b1 = 0 dan b2 = 11 atau b1 = -1 dan b2 = 12. Sedangkan parameter c1 dan a2 akan mengalami pergeseran nilai, hal ini dikarenakan kedua parameter tersebut mempengaruhi panjang lebar garis kurva di dalam rentang data inputan yang secara langsung juga mempengaruhi nilai Belief dalam tahap fuzzifikasi. Sedangkan parameter a1 dan c2 juga bergeser mengkuti perubahan c1 dan a2 agar bentuk kurva tetap simetris. Kedua parameter ini tidak berpengaruh karena berada diluar rentangan data inputan.
Pada bentuk bell ini parameter yang berubah adalah parameter lebar kurva (a) dan tingkat kemiringan kurva (b). Dimana untuk satu nilai parameter a1 dan a2 akan diuji dengan sepuluh parameter b1 dan b2 yang berbeda. Nilai parameter a1 = a2 serta nilai b1 = b2 untuk setiap percobaan agar bentuk MF bell tetap simetris.
Tabel 7. Parameter MF Bell Titik Pusat 0 dan 11
|
Percobaan ke- |
Nilai Parameter yang Digunakan | |||||
|
a1 |
b1 |
c1 |
a2 |
b2 |
c2 | |
|
1 |
1 |
1 |
0 |
1 |
1 |
11 |
|
2 |
1 |
2 |
0 |
1 |
2 |
11 |
|
3 |
1 |
3 |
0 |
1 |
3 |
11 |
|
. . dst. |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
70 |
7 |
10 |
0 |
7 |
10 |
11 |
Tabel 8. Parameter MF Bell Titik Pusat -1 dan 12
|
Percobaan ke- |
Nilai Parameter yang Digunakan | |||||
|
a1 |
b1 |
c1 |
a2 |
b2 |
c2 | |
|
1 |
1 |
1 |
-1 |
1 |
1 |
12 |
|
2 |
1 |
2 |
-1 |
1 |
2 |
12 |
|
3 |
1 |
3 |
-1 |
1 |
3 |
12 |
|
. . dst. |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
70 |
7 |
10 |
-1 |
7 |
10 |
12 |
Perubahan nilai parameter a adalah dari 1 sampai 7, parameter b dari 1 sampai 10, sedangkan parameter c1 dan c2 tidak berubah. Parameter a dilakukan percobaan sampai 7 karena semakin besar nilai a maka kurva bell akan semakin lebar sampai menutupi daerah data inputan seperti garis lurus. Sedangkan parameter b dilakukan percobaan sampai 10 karena semakin besar nilai b maka semakin tegak dan lurus kurva bell tersebut.
Klasifikasi menggunakan MF segitiga dibagi menjadi dua bagian utama, yaitu bagian pertama adalah dengan menggunakan parameter titik pusat kurva di dalam rentang data dan diluar rentang data.
Grafik Tingkat Akurasi MF Segitiga
b1=1 dan b2=10
-
76.20% 76.13%
-
76.10% 75.99% 75.99% 75.99%
2 76.00% • ∙ ∙ ”•“ c1 = 10
I 75.90% 75.84% —•— c1 = 9
≤ 75.80% —c1 = 8
-
75.70% —c1 = 7
75.60%
1
—•— c1 = 6
2345
Parameter a2
Gambar 6. Grafik MF Segitiga dalam Rentang Data
Grafik Tingkat Akurasi MF Segitiga b1=0 dan b2=11
-
86.50% 86.38%86.38%
∙C5 86.40% • ∙ __________________
(U 86.24%86.24%86.24%
D 86.30%
< 86.20% 86.09%
Tu 86.10% —•—
⅛ 86.00%
—•—c1 = 11
—•—c1 = 10
—•—c1 = 9
—•—c1 = 8
85.90%
0
12345
Parameter a2
—^c1 = 7
—^c1 = 6
Gambar 7. Grafik MF Segitiga Titik Pusat 0 dan 11
|
Grafik Tingkat Akurasi MF Segitiga b1 = -1 dan b2 = 12 86.30% 86.24%86.24%86.24% 86.24%86.24% ∙ ∙ ∙ ∙ ∙ —c1 = 12 | |
|
∖λ ro < 76 Z |
85.80% —•— c1 = 8 85.70%
|
Parameter a2 —•— c1 = 6
Gambar 8. Grafik MF Segitiga Titik Pusat -1 dan 12
Parameter c1 adalah parameter titik akhir kurva kelas normal dan a2 adalah parameter titik mulai kurva kelas abnormal. Grafik ini hanya menggunakan kedua parameter tersebut untuk menunjukkan tingkat akurasi karena perubahan atau pergeseran kedua parameter itulah yang mempengaruhi perubahan nilai Belief yang kemudian akan mempengaruhi nilai keyakinan setiap kelas pada perhitungan Dempster – Shafer. Dapat dilihat pada Gambar 6 bahwa dengan menggunakan parameter dalam rentang data cenderung menghasilkan nilai akurasi yang menurun seiring dengan pergeseran parameter c1 dan a2. Nilai akurasi yang paling baik adalah 76,13% dengan menggunakan parameter b1 = 1, c1 = 10, b2 = 10, dan a2 = 1. Sedangkan berdasarkan Gambar 7 dengan menggunakan titik pusat diluar rentang data menghasilkan nilai akurasi yang paling baik adalah 86,38% pada parameter b1 = 0, b2 = 11, c1 = 11 dan c1 = 10, a2 = 0 dan a2 = 1. Antara parameter di dalam rentang dan diluar data, hasil akurasi yang lebih baik adalah menggunakan parameter diluar rentang data dimana di dalam rentang mendapatkan akurasi 76,13% sedangkan diluar rentang data 86,38%.
Lalu pada percobaan selanjutnya adalah masih menggunakan parameter diluar rentang data tetapi titik pusat kurva berpindah lebih jauh, yaitu b1 = -1 dan b2 = 12. Hasil percobaan ini dapat dilihat pada Gambar 8 dimana nilai akurasi yang paling baik adalah 86,24% pada parameter b1 = -1, b2 = 12 dan parameter c1 dari nilai 12, 10, 11, 7, dan 6 serta parameter a2 dari nilai -1, 0, 1, 4, dan 5.
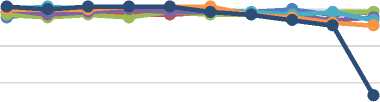
Gambar 9 menunjukkan grafik tingkat akurasi menggunakan parameter titik pusat dalam rentang data, yaitu c1 = 1 (titik pusat kurva kelas normal) dan c2 = 10 (titik pusat kurva kelas abnormal). Dapat dilihat bahwa dengan menggunakan parameter dalam rentang data cenderung menghasilkan nilai akurasi yang menurun seiring dengan pergeseran parameter a dan b. Nilai akurasi yang paling baik adalah 76,13% dengan menggunakan parameter b1 dan b2 pada nilai 4 dan 5, parameter a1 dan a2 pada nilai 5, 6, dan 7.
Selanjutnya pada Gambar 10 adalah hasil akurasi menggunakan parameter diluar rentang data cenderung menghasilkan nilai akurasi yang meningkat seiring dengan perubahan parameter a dan b. Nilai akurasi yang paling baik adalah 88,87% pada penggunaan parameter a1 = a2 = 4 dan b1 = b2 = 10. Antara penggunaan parameter titik pusat kurva di dalam dan diluar rentang data menghasilkan nilai akurasi yang cukup berbeda. Pada parameter titik pusat kurva di dalam menghasilkan nilai akurasi 76,13% sedangkan penggunaan parameter titik pusat kurva diluar rentang data menghasilkan nilai akurasi yang lebih besar, yaitu 88,87%.
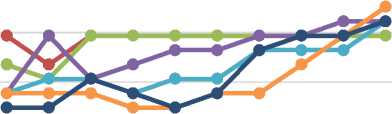
Kemudian dilakukan percobaan penggunaan parameter titik pusat kurva diluar rentang data yang lebih jauh, yaitu c1 = -1 dan c2 = 12. Hasil percobaan dapat dilihat pada Gambar 11 cenderung meningkat dan pada penggunaan parameter a1 = a2 = 1 dan a1 = a2 = 2 memiliki nilai akurasi sama. Nilai akurasi paling besar adalah 87,26% pada parameter a1 = a2 = 6 dan b1 = b2 = 10. Dari ketiga jenis percobaan pada bentuk MF bell, dihasilkan nilai akurasi yang paling baik pada penggunaan parameter titik pusat diluar rentang data sebesar 88,87% dengan menggunakan parameter a1 = a2 = 4, b1 = b2 = 10, c1 = 0, dan c2 = 11.
Grafik Tingkat Akurasi MF Bell c1 = 1 dan c2 = 10
78.00%
76.00%
GH CU
⊃ 74.00%
<
ra 72.00%
70.00%
68.00%
1 2 3 4 5 6 7 8 9 10
Parameter b1 dan b2
Parameter a1 dan a2
—•— 1
—•— 2
—•— 3
—•— 4
—•— 5
—•— 6
—•— 7
Gambar 9. Akurasi MF Bell dalam Rentang Data
Grafik Tingkat Akurasi MF Bell c1 = 0 dan c2 = 11
Parameter a1 dan a2
—•— 1
—•— 2
—•— 3
—•— 4
—•— 5
—•— 6
90.00%

85.00%
GH
CU
J∣ 80.00%
<
≤ 75.00%
70.00%
65.00%
1 2 3 4 5 6 7 8 9 10
Parameter b1 dan b2
Gambar 10. Akurasi MF Bell Titik Pusat 0 dan 11
Grafik Tingkat Akurasi MF Bell c1 = -1 dan c2 = 12
Parameter a1 dan a2
—•— 1
—•— 2
—•— 3
—•— 4
—•— 5
—•— 6
—•— 7
87.50%
*(Λ 87.00%
CU
ZS
< 86.50%
≡ 86.00%
85.50%
1 2 3 4 5 6 7 8 9 10
Parameter b1 dan b2
Gambar 11. Akurasi MF Bell Titik Pusat -1 dan 12
Dari penelitian yang dilakukan, diperoleh kesimpulan sebagai berikut:
-
1. Hasil perbandingan parameter titik pusat kurva Membership Function (MF) menunjukkan bahwa menggunakan titik pusat di luar rentang data menghasilkan nilai akurasi yang lebih baik. Parameter yang optimal bagi bentuk MF segitiga adalah a1 = a2 = 4, b1 = b2 = 10, c1 = 0 dan c2 = 11 dan bentuk MF bell adalah a1 = -11, b1 = 0, c1 = 11 dan a2 = 0, b2 = 1, c2 = 22.
-
2. Hasil penelitian menunjukkan bahwa bentuk MF bell dengan akurasi 88,87% lebih baik daripada MF segitiga dengan akurasi 86,38%. Penggunaan bentuk Membership Function (MF) yang berbeda dan dengan parameter yang berubah – ubah akan menghasilkan nilai Belief yang berbeda – beda pula dan di saat yang bersamaan mempengaruhi tingkat akurasi.
Data Pustaka
-
[1] C. C. Aggarwal, Data Classification: Algorithms and Applications. CRC press, 2014.
-
[2] G. Klir and B. Yuan, Fuzzy Sets and Fuzzy Logic. Prentice hall New Jersey, 1995.
-
[3] M. Muliadi, I. Budiman, M. A. Pratama, and A. Sofyan, "Fuzzy Dan Dempster-Shafer
Pada Sistem Pakar Diagnosa Penyakit Tanaman Cabai," vol. 4, no. 2, pp. 209-222, 2017.
-
[4] J. Zhao and B. K. Bose, "Evaluation Of Membership Functions For Fuzzy Logic Controlled
Induction Motor Drive " in IEEE 2002 28th Annual Conference of the Industrial Electronics Society. IECON 02, 2002, vol. 1, pp. 229-234: IEEE.
-
[5] A. F. Mashaly and A. A. Alazba, "Membership Function Comparative Investigation on
Productivity Forecasting of Solar Still Using Adaptive Neuro-Fuzzy Inference System Approach," vol. 37, no. 1, pp. 249-259, 2018.
-
[6] B. Shinkins and R. Perera, "Diagnostic uncertainty: dichotomies are not the answer," ed:
British Journal of General Practice, 2013.
-
[7] A. Sadollah, Fuzzy Logic Based in Optimization Methods and Control Systems and Its
Applications. BoD–Books on Demand, 2018.
-
[8] C. L. Blake and C. J. Merz. (1998). UCI Repository of Machine Learning Databases,
1998. Available: http://www.ics.uci.edu/~mlearn/MLRepository.html
-
[9] H. Nasution, "Implementasi Logika Fuzzy pada Sistem Kecerdasan Buatan," vol. 4, no.
-
2, 2012.
-
[10] L. A. Zadeh, "Fuzzy sets," vol. 8, no. 3, pp. 338-353, 1965.
-
[11] S. Kusumadewi and I. Guswaludin, "Fuzzy Multi-Criteria Decision Making," vol. 3, no. 1,
2005.
-
[12] B. K. Bose, Modern power electronics and AC drives. Prentice hall Upper Saddle River,
NJ, 2002.
-
[13] M. Dahria, R. Silalahi, and M. J. U. T. D. Ramadhan, Medan, "Sistem Pakar Metode
Dampster Shafer Untuk Menentukan Jenis Gangguan Perkembangan Pada Anak," 2013.
89
Discussion and feedback