OPTIMASI TRAVELING SALESMAN PROBLEM (TSP) UNTUK RUTE PAKET WISATA DI BALI DENGAN ALGORITMA GENETIKA
on
Jurnal Ilmiah
ILMU KOMPUTER
Universitas Udayana
Vol. X, No. 1, April 2017
ISSN 1979 - 5661
OPTIMASI TRAVELING SALESMAN PROBLEM (TSP) UNTUK RUTE PAKET WISATA DI BALI DENGAN ALGORITMA GENETIKA
Luh Gede Ayu Candrawati1, Gusti Agung Gede Arya Kadyanan 2
1, 2Program Studi Teknik Informatika, Jurusan Ilmu Komputer, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana E-mail: ayucandrawatii@gmail.com1, gungde.arya@gmail.com2
ABSTRAK
Bali merupakan salah satu destinasi favorit bagi wisatawan mancanegara. Biasanya perusahaan jasa atau hotel tempat menginap bagi wisatawan menawarkan berbagai macam paket wisata. Akan tetapi ada wisatawan yang merasa kurang puas terhadap paket-paket wisata yang ditawarkan. Hal ini dikarenakan tempat yang ingin dikunjungi tidak sesuai dengan tempat yang mereka inginkan. Selain itu juga karena terbatasanya waktu yang dimiliki wisatawan untuk berlibur di Bali berbanding terbalik dengan banyaknya destinasi wisata yang ada di Bali. Yang terakhir adalah karena kepadatan lalu lintas yang berbeda tiap waktu sehingga waktu yang dimiliki oleh wisatawan menjadi semakin sempit. Untuk itu penulis mencoba memecahkan masalah ini yaitu dengan mengoptimasi rute dan penjadwalan paket wisata di Bali menggunakan algoritma genetika. Sehingga pada peneiltian ini dapat menghasilkan penjadwalan perjalanan paling optimal dengan mempertimbangkan rute terpendek di Pulau Bali.
Kata Kunci: Optimasi Rute, Traveling Salesman Problem, Algoritma Genetika
ABSTRACT
Bali is a favorite destination for foreign tourists. Usually a service company or hotel accommodation for tourists offer a variety of tour packages. But there are tourists who feel less satisfied with the tour packages offered. This is because the places you want to visit is not in accordance with the place they want. In addition, because the time owned terbatasanya tourists to vacation in Bali is inversely proportional to the number of tourist destinations in Bali. The latter is due to the density of traffic is different each time so that time owned by tourists become increasingly narrow. To the authors tried to solve this problem is to optimize the scheduling of routes and travel packages in Bali using genetic algorithms. So at this peneiltian can produce the most optimal trip scheduling by considering the shortest route on the island of Bali.
Keywords: Route Optimization, Traveling Salesman Problem, Genetic Algorithm
Pulau Bali dikenal juga dengan pulau dewata. Salah satu hal yang identik dengan pulau ini adalah sektor pariwisatanya. Pariwisata di Bali menyediakan berbagai macam tempat
wisata yang menarik untuk dikunjungi oleh wisatawan. Terdapat ratusan bahkan ribuan destinasi wisata di pulau ini. Wisata alam, wisata budaya hingga wisata spiritual pun tersedia disini. Pulau Bali menjadi salah satu tujuan destinasi wisata favorit bagi para traveler dikancah dunia Internasional.
Menurut data Badan Pusat Statistik Provinsi Bali wisatawan mancanegara yang berkunjung ke pulau ini mencapai 4.927.937 orang pada tahun 2016[1]. Hal ini tentu menjadi peluang bagi perusahan jasa atau hotel untuk menyediakan paket wisata di Bali.
Pada tiap paket wisata, rute perjalanan dan tempat wisata sudah ditentukan oleh perusahaan jasa atau hotel tempat wisatawan menginap. Sering kali wisatawan merasa kurang puas terhadap paket wisata tersebut. Banyak faktor yang menyebabkan hal itu terjadi. Yang pertama adalah keterbatasan waktu liburan yang dimiliki wisatawan. Yang kedua, banyaknya tempat wisata yang ada di Bali. Yang ketiga, ketidaksesuaian tempat wisata yang ingin dikunjungi oleh wisatawan. Yang terakhir adalah karena kepadatan lalu lintas yang berbeda-beda tiap waktu. Banyak wisatawan beralih berwisata backpacker. Dengan berwisata backpacker para wisatawan akan lebih leluasa memilih tujuan wisata yang mereka inginkan. Namun tetap saja waktu yang terbatas dan banyaknya tempat wisata yang dipilih mengharuskan para wisatawan menjadwalkan perjalanan wisata menjadi seefektif dan seefisien mungkin.
Berdasarkan permasalahan yang telah diuraikan, maka diperlukan solusi yang tepat untuk memecahkan masalah tersebut. Sebuah sistem yang dapat menentukan rute dan penjadwalan paket wisata. Untuk menentukan rute dan penjadwalan paket wisata dibuat berdasarkan jarak antar tempat wisata dengan algoritma genetika.
Permasalahan matematika adalah cikal bakal dari permasalahan Travelling Salesman Problem (TSP), dikemukakan oleh matematikawan Irlandia William Rowan Hamilton dan matematikawan Inggris Thomas Penyngton pada tahun 1800. Matematikawan Karl Menger di Vienna dan Harvard pada tahun 1930 mempelajari pertama kali bentuk umum
dari Travelling Salesman Problem. Kemudian Hassler Whitney dan Merrill Flood di Princeton adalah orang yang mempublikasikan permasalahan ini. Pembicaraan detail tentang hubungan antara Menger dan Whitney, dan perkembangan dari TSP sebagai topik studi dapat dilihat di makalah Alexander Schrijver yang berjudul “On the history of combinatorial optimization (till 1960)” [2].
Definisi dari Traveling Salesman Problem adalah permasalahan untuk mencari biaya tour minimal dari sekumpulan kota, dimana tiap kotanya hanya dikunjungi satu kali (Pesant, 1998). Dalam Traveling Salesman Problem berhubungan dengan total jarak travel (total jarak destinasi wisata yang dituju). Traveling Salesman Problem memiliki bobot sisi minimum, dimana bobot pada sisi adalah jarak dimana dengan menentukan jarak yang terpendek. Dalam penelitian ini konsep Traveling Salesman Problem dengan mengansumsikan setiap wisatawan memulai dan mengakhiri perjalanan wisatanya dari hotel tempat mereka menginap. Setiap destinasi wisata hanya dikunjungi satu kali pada tiap paketnya. Dalam proses pencarian rute, terlebih dahulu harus mengetahui jarak antar destinasi wisata.

Gambar 1. Titik-titik destinasi wisata yang akan dilewati
Setelah jarak yang menghubungkan tiap destinasi wisata diketahui, maka rute terpendek dapat dicari dengan mencoba semua kombinasi dan menjumlahkan jarak dari kombinasi tersebut sehinga didapatkan rute seperti pada gambar 2.
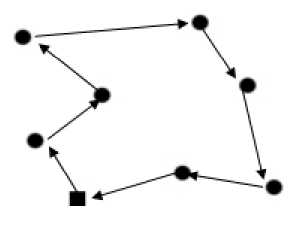
Gambar 2. Rute terpendek destinasi wisata yang didapatkan
Algoritma genetika adalah
percabangan dari Algoritma Evolusi. Algoritma genetika adalah algoritma yang menggunakan prinsip atau konsep seleksi alam yang ada dalam ilmu genetika guna mengembangkan solusi terhadap
permasalahan (Haupt, 2004). Algoritma genetika merupakan metode adaptive yang biasa digunakan untuk memecahkan suatu pencarian nilai dalam sebuah masalah optimasi. Algoritma ini didasarkan pada proses genetik yang ada dalam makhluk hidup dengan prinsipnya yaitu seleksi alam. Algoritma ini bekerja dengan sebuah populasi yang terdiri dari individu-individu yang tiap individu mempresentasikan sebuah solusi yang mungkin bagi persoalan yang ada. Masing-masing individu dilambangkan dengan sebuah nilai fitness yang akan digunakan untuk mencari solusi terbaik dari persoalan yang ada berdasarkan nilai fitness tertinggi dari semua generasi.
Hasil akhir dari algortima genetika adalah menampilkan kromosom yang memiliki nilai fitness tertinggi dari semua generasi. Parameter algoritma genetik yang digunakan pada penelitian ini adalah:
-
a. PopSize, yaitu banyaknya individu
yang dilibatkan pada setiap generasi.
-
b. Crossover Rate (Cr), adalah
kemungkinan terjadinya
persilangan (crossover) pada suatu generasi.
-
c. Mutation Rate (Mr), adalah kemungkinan terjadinya mutasi pada setiap individu.
-
d. Banyaknya generasi yang akan dibentuk dimana akan menentukan lama penerapan algoritma genetik.
Tiap anggota populasi disebut dengan kromosom. Kromosom adalah solusi dari masalah yang dihadapi. Untuk mendapatkan kromosom yang baik yaitu dengan cara kawin silang dan mutasi. Representasi chromosome yang digunakan untuk algoritma genetika pada penelitian ini adalah representasi permutasi. Dalam satu individu terdapat beberapa gen yang direpresentasikan dalam bentuk angka-angka. Dalam penelitian ini, setiap angka dalam setiap kromosom akan mewakili destinasi-destinasi wisata. Satu kromosom atau susunan gen akan mewakili sebuah urutan destinasi wisata mana yang akan di kunjungi terlebih dahulu.
Nilai fitness adalah nilai yang menyatakan baik tidaknya suatu solusi (individu). Semakin tinggi nilai fitness maka semakin tinggi nilai kromosom. Dalam penelitian ini nilai fitness adalah untuk persamaan.
::i'7:.i-i-:€ii = ---—— (1)
H,cyJ+iPt
dimana:
-
- Cij adalah jarak tempuh dari titik i ke titik j.
-
- pi merupakan penalti jika wisatawan mengunjungi tempat wisata diluar waktu buka/terbaik.
-
2.2.3 Crossover
Crossover (pindah silang)
merupakan salah satu operator dalam algoritma genetika yang melibatkan dua buah induk untuk menghasilkan keturunan baru. Cara kerja crossover adalah dengan membangkitkan offspring baru dengan mengganti sebagian informasi dari parents[3]. Pada penelitian ini akan digunakan metode partially matched crossover (PMX) karena metode ini dapat mencegah adanya gen ganda pada suatu individu.
Mutasi adalah proses untuk
menciptakan individu baru dengan
memodifikasi gen dalam suatu individu. Mutasi akan meningkatkan variasi populasi dengan mengganti gen yang hilang dari populasi selama proses seleksi serta menyediakan gen yang tidak ada dalam populasi awal. Pada penelitian menggunakan metode mutasi reciprocal exchange. Metode mutasi reciprocal exchange tidak akan menghasilkan gen yang sama pada anaknya dimana cara kerjanya adalah dengan memilih dua posisi secara random, kemudian menukar kedua posisi tersebut.
Seleksi adalah proses pemilihan calon induk. Pada penelitian ini akan dilakukan perbandingan dua metode seleksi yaitu Roulette Wheel dan Elitism. Konsep kerja metode Roulette Wheel sama seperti sebuah roda roulette dengan isi kemungkinan adalah semua kromosom. Besarnya nilai kemungkinan bagi setiap kromosom adalah tergantung dari nilai fitnessnya. Dari konsep kerja metode ini, semakin baik nilai fitness-nya maka semakin besar kemungkinannya untuk terpilih. Metode Seleksi Elitis adalah Metode dengan mempertahankan individu-individu yang mempunyai nilai fitness tinggi untuk menjadi generasi selanjutnya. Individu yang telah dipertahankan akan dibandingkan dengan individu hasil proses regenerasi.
Metodelogi yang digunakan pada penelitian ini dapat digambarkan dengan diagram fishbone seperti berikut :
Pada diagram diatas dapat kita lihat bahwa sistem ini mulai dibuat berawal dari permasalahan seperti yang ada pada gambar diatas dan dibuat melalui tahapan-tahapan yang pada akhirnya akan menghasilkan sebuah sistem.
Dalam penelitian ini dilakukan dengan menggunakan data sejumlah 7 destinasi wisata yang diambil secara acak dari daftar destinasi wisata yang ada di Bali. Tiap destinasi wisata lama kunjungannya adalah 2 jam. Dan kecepatan perjalanan antar destinasi wisata adalah 60 km/jam. Berikut merupakan tabel daftar wista di Bali.
Tabel 1. Daftar Wisata di Bali
|
Tujuan Wisata |
Lama Kunjungan (jam) |
Kecepatan (km/jam) |
|
Gunung Kawi |
2 |
60 |
|
Tanah Lot |
2 |
60 |
|
Jatiluwih |
2 |
60 |
|
Kintamani |
2 |
60 |
|
Danau Beratan |
2 |
60 |
|
Goa Lawah |
2 |
60 |
|
Taman Ayun |
2 |
60 |
Pada tabel diatas dipilih beberapa destinasi wisata yang ada di Bali sebagai sampel. Penerapan aplikasi pada penelitian ini, destinasi tersebut dipilih secara acak oleh sistem sesuai dengan jarak terdekat dari hotel atau tempat wistawan menginap. Berikut merupakan contoh destinasi wisata (gen) yang terlah diacak oleh sistem yang dikelompokan pada masing-masing kromosom.

Gambar 3. Diagram Fishbone
Tabel 2. Contoh individu dan susunan gen pada kromosom
|
Individu |
Kromosom | ||||||
|
K1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
K2 |
1 |
3 |
2 |
7 |
4 |
5 |
6 |
|
K3 |
1 |
7 |
5 |
4 |
6 |
3 |
2 |
Pada tabel diatas destinasi wisata (gen) di simbolkan dengan angka yang disusun pada sebuah kromosom.
Adapun flowchart dari sistem pada penelitian ini adalah sebagai berikut :

Gambar 4. Flowchart sistem
Proses pencarian rute destinasi wisata dengan algoritma genetika adalah seperti pada flowchart gambar 4. Poses pertama adalah menganalisa parameter apa saja yang akan digunakan. Setelah itu membuat populasi sesuai dengan panjang kromosom yaitu banyaknya destinasi yang akan dituju. Setelah itu melakukan crossover dan mutasi untuk diambil dan dijadikan sebagai calon induk. Setelah itu menghitung nilai fitness. Proses pemilihan kromosom terbaik yaitu dengan cara membandingkan nilai fitness terbaik pada setiap generasi. Proses selanjutnya adalah menyimpan kromosom terbaik. Hasil akhir dari algoritma genetika adalah menapilkan kromosom dengan nilai fitness terbaik.
Pada tahap ini dilakukan dengan penerapan algoritma genetika untuk paket
wisata di Bali. Sistem ini dibuat dengan menggunakan bahasa PHP. Sistem ini merupakan sebuah sistem yang dinamis dan hanya menginputkan jarak antar destinasi wisata. Berikut tampilan halaman utama pada sistem.

Gambar 5. Tampilan halaman utama
Gambar diatas merupakan tampilan halaman utama pada sistem. Pada sistem ini tiap kromosom terdapat 7 gen. Jumlah populasi, maksimal generasi, dan elitism bisa disesuaikan dengan kebutuhan. Akan tetapi pada percobaan ini jumlah populasi diset menjadi 50, maksimal generasi diset menjadi 100 generasi, dan elitism diset menjadi 1. Untuk jarak antar destinasi wisata diinputkan sesuai dengan kebutuhan. Adapun contoh perhitungan untuk 1 populasi adalah sebagai berikut :
-
a) Menentukan populasi
-
b) Menghitung nilai fitness
AB+BC+CE+EF+FG+GD+DA = 11
AB+BC+CF+FG+GD+DE+EA = 14
AB+BG+GF+FE+ED+DC+CA = 12
AC+CB+BE+ED+DF+FG+GA = 16
AD+DB+BC+CE+EF+FG+GA = 16
-
c) Menetukan nilai roullete
Kromosom 1 = 11/69 = 0,159
Kromosom 2 = 14/69 = 0,202
Kromosom 3 = 12/69 = 0,173
Kromosom 4 = 16/69 = 0,231
Kromosom 5 = 16/69 = 0,231
Kromosom 1 = 16%
Kromosom 2 = 20%
Kromosom 3 = 18%
Kromosom 4 = 23%
Kromosom 5 = 23%
R1 = 10
R2 = 91
R3 = 29
R4 = 50
R5 = 99
Kromosom 1 = 1 = [A B C E F GD]
Kromosom 2 = 5 = [A D B C E FG]
Kromosom 3 = 2 = [A B C F G DE]
Kromosom 4 = 3 = [A B G F E DC]
Kromosom 5 = 5 = [A D B C E FG]
-
d) Melakukan crossover
Kromosom 1 = [A B C E F G D]
Kromosom 5= [A D B C E G F]
Child 1 = [A D B C E G F]
-
e) Melakukan mutasi
Range 1-49
Mutasi 1%
Random = 20 -> gen ke 20
Range 1-7
Random = 2
Kromosom3 = [ A D C F G B E ]
-
f) Menghitung fitness
Child 1 = [A D B C E G F]
Child 1 = AD + DB +BC + CE + EG +
GF + FA = 13
-
g) Hasil generasi baru
Kromosom 1 = 11
Kromosom 2 = 14
Kromosom 3 = 12
Kromosom 5 = 16
Child 1 = 13
Pada sistem ini akan menghitung secara otomatis jarak mana yang paling pendek yang nantinya akan menjadi hasil akhir dari perhitungan pada sistem dan iiterasi akan berhenti ketika urutan destinasi wisata pada masing-masing kromoson sama.
Berdasarkan dari penelitian yang telah dilakukan maka dapat disimpulkan bahwa, penggunaan algoritma Genetika dapat digunakan dalam menetukan rute terpendek untuk menetukan destinasi wisata di Bali dengan parameter-parameter yang digunakan adalah crossover dengan metode partially matched crossover (PMX), mutasi dengan metode mutasi reciprocal exchange, seleksi dengan metode Roulette Wheel dan Elitism.
-
[1] Kementerian Pariwisata Republik Indonesia.Destinasi Wisata Indonesia: Bali. 2016. URL:https://bali.bps.go.id
-
[2] History of the TSP. 2007.
URL:http://www.math.uwaterloo.ca/ts p/history/
-
[3] Dwi.N.,Firdaus.W. 2015. "Optimasi Traveling Salesman Problem with Time Windows (TSP-TW) Pada Penjadwalan Rute Wisata di Pulau Bali Menggunakan Algoritma Genetika". Seminar Nasional Sistem Informasi Indonesia. 2-3 November 2015.
-
[4] Mahmudy, W. F., 2013. Modul
Matakuliah Algoritma Evolusi. Malang: Program Teknologi Informasi dan Ilmu Komputer Universitas Brawijaya.
-
[5] Anonim. 2006. Tentang Kami,
<URL:
https://www.waze.com/id/about>.
-
[6] Widodo, W. A., & Mahmudy, W. F. 2010. Penerapan Algoritma Genetika Pada Sistem Rekomendasi Wisata Kuliner., Jurnal Ilmiah KURSOR. Vol. 5, No. 4, Juli 2010
Discussion and feedback