RANCANGAN ARSITEKTUR SARBAGITA-APPS : APLIKASI BERBASIS MOBILE UNTUK MEMBANTU PEMILIHAN RUTE BAGI PENGGUNA BUS SARBAGITA MENGGUNAKAN TEORI GRAPH
on
Jurnal Ilmiah
ILMU KOMPUTER
Universitas Udayana
Vol. X, No. 2, September 2017
ISSN 1979 - 5661
RANCANGAN ARSITEKTUR SARBAGITA-APPS : APLIKASI BERBASIS MOBILE UNTUK MEMBANTU PEMILIHAN RUTE BAGI PENGGUNA BUS SARBAGITA MENGGUNAKAN TEORI GRAPH
I Gede Oka Gartria Atitama 1
Program Studi Teknik Informatika, Jurusan Ilmu Komputer, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana
E-mail: oka.gartria@cs.unud.ac.id1
ABSTRAK
Aplikasi Sarbagita-Apps merupakan aplikasi yang diharapkan dapat digunakan dalam menyediakan informasi mengenai rute dan lokasi dari halte bus sarbagita yang terdekat dari lokasi pengguna. Untuk membangun aplikasi ini, rute bus Sarbagita direpresentasikan dalam sebuah bidirectional graph. Pada pengembangannya, Sarbagita-Apps akan menggunakan Metode Haversine untuk menentukan lokasi halte terdekat dari pengguna. Untuk mencari rute ke halte tujuan digunakan Algoritma Dijkstra.
Kata Kunci: Sarbagita,bus, mobile, graph, haversine, dijkstra
ABSTRACT
Sarbagita-Apps is an application that will provide information about the nearby shelter and route of Sarbagita Bus.In this application, Sarbagita Bus routes are represented by using bidirectional graph. In its development, Sarbagita-Apps will use haversine method to finding nearby bus shelter from user. Dijkstra algorithm will use for search route to destination bus shelter.
Keywords: Sarbagita,bus, mobile, graph, haversine, dijkstra
Bus Sarbagita merupakan moda transportasi umum masal dimunculkan oleh pemerintah provinsi Bali sebagai salah satu cara mengurangi kemacetan. Rute yang dilalui oleh bus ini umumnya dekat dengan fasilitas umum dan destinasi wisata yang ada di Bali, khususnya di kawasan Denpasar, Badung, Gianyar dan Tabanan (SARBAGITA).
Keberadaan bus sarbagita sebagai moda transportasi darat masal belum optimal. Salah satu penyebabnya adalah kurangnya sosialisasi bagi pengguna baru. Pengguna baru umumnya belum mengetahui rute serta posisi halte yang dapat mengantarkan ke tujuan.
Melihat permasalahan tersebut, kami melihat kesempatan dalam menangani permasalahan ini dengan memanfaatkan teknologi smartphone yang saat ini sudah
menjadi trend tersendiri. Dengan teknologi GPS yang sudah tertanam pada smartphone kami bermaksud membuat sebuah aplikasi yang bertujuan menyediakan informasi mengenai rute dan lokasi dari halte bus sarbagita yang terdekat bagi penggunanya.
Penelitian mengenai sistem transportasi publik yang pintar (Intelligent urban transportation systems) sangat penting untuk menunjang visi smart city. Beberapa penelitian terkait telah dilakukan untuk mewujudkan sistem ini. Salah satu masalah utama yang diteliti dalam penerapan sistem ini adalah mencari rute yang optimal dari titik asal ke tempat tujuan diantara sekumpulan rute yang ada pada jaringan transportasi publik yang tersedia (Ni, Vo, Dahlmeier, Ivanchev, & Aydt, 2015).
Dalam mencari rute optimal pada jaringan transportasi publik dengan cepat beberapa penelitian telah dilakukan. Penelitian tersebut, umumnya menggunakan teknik dasar dari algoritma Dijkstra untuk menemukan rute yang optimal dari suatu titik asal ke tempat tujuan (Bast, et al., 2016).
Beberapa penelitian mengenai pencarian rute optimal untuk sistem transportasi publik juga telah dilakukan di Indonesia. Sofyan et al. dalam tesisnya mengembangkan sistem untuk menentukan
rute transportasi umum multimoda di Jakarta. Pada penelitiannya Sofyan et al. menggunakan algoritma Dijkstra untuk menemukan rute yang optimal (Sofyan, Suryono, & Suhartono, 2012). Muhammad Irawan dalam penelitiannya juga menggunakan algoritma Dijkstra dalam mencari rute optimal untuk angkot di Bogor (Irawan, 2013). Penelitian mengenai pencarian rute optimal untuk bus Trans Semarang dilakukan oleh Ardana & Saputra menggunakan Dijkstra (Ardana & Saputra, 2016).
Dalam penelitian ini akan memanfaatkan GPS Receiver yang tertanam pada smartphone. GPS atau Global Positioning System adalah sistem navigasi radio berbasis satelit yang dimiliki oleh Pemerintah Amerika Serikat (U.S. Air Force, 2017). GPS adalah salah satu dari beberapa sistem navigasi satelit di dunia yang memberikan informasi geolokasi dan juga waktu. Selain GPS, beberapa sistem navigasi satelit atau Global Navigation Satellite System (GNSS) adalah GLONASS milik Rusia, Galileo milik Eropa, dan BeiDou milik Cina.
GNSS Receiver adalah receiver untuk menerima data dari satelit GNSS. Pada smartphone, umumnya GNSS Receiver yang tertanam hanya dapat menerima data dari GPS milik Amerika, sehingga sering disebut GPS Receiver. GPS terdiri dari 24 atau lebih satelit

Gambar 1 Cara Kerja GPS (U.S. Air Force, 2017)
Gambar 1 menunjukkan cara kerja GPS secara umum. Adapun cara kerjanya adalah :
-
1. Satelit GPS akan mengirimkan data secara broadcast yang berisi lokasi, status dan waktu dari jam atom yang ada pada satelit
-
2. Sinyal GPS kemudian mengirimkan data tersebut dengan kecepatan cahaya
pengguna aplikasi. Dari posisi pengguna tersebut, kemudian akan dicari lokasi halte yang paling dekat dengan pengguna. Metode yang digunakan untuk mencari jarak antara posisi pengguna dan lokasi halte adalah metode haversine.

Gambar 2 Ilustrasi jarak orthodomic antara titik P dan Q
Metode haversine adalah metode yang dapat digunakan untuk mencari jarak antara 2 titik pada bangun ruang bola berdasarkan garis lintang (longitude) dan

-
3. GPS Receiver menerima data dari satelit dan mencatat waktu penerimaan data yang akan digunakan untuk menentukan jarak antara receiver dengan satelit.
-
4. Jika GPS Receiver telah menerima data dan mendapatkan jarak dari minimal 4 satelit, GPS receiver dapat
menggunakan rumus geometri untuk menentukan lokasi pada bumi.
Pemanfaatan GPS pada penelitian ini adalah untuk mengetahui posisi dari
garis bujur (latitude). Untuk bentuk berupa bola, jarak yang didapatkan antara dua titik pada bola terebut adalah jarak orthodromic atau jarak lingkaran terbesar. Gambar 2 menggambarkan ilustrasi jarak lingkaran terbesar atau jarak orthodromic dari titik P dan Q (Mwemezi & Huang, 2011).
Untuk mencari jarak antara dua titik pada bumi menggunakan metode haversine, diasumsikan bumi berbentuk bola yang sempurna. Dengan jari – jari bumi r 6.367,45 km, dan posisi dari kedua titik masing – masing pada koordinat bujur dan
lintang γ1, φ1, dan γ2, φ2, maka jarak kedua titik tersebut dapat dicari dengan metode haversine seperti pada Persamaan 1.
Dalam bidang ilmu komputer, permasalahan pencarian rute dianalogikan sebagai sebuah graph. Graph merupakan sebuah representasi dari sebuah grup objek yang disebut verteks, dan verteks tersebut dapat terhubung satu sama lain oleh sebuah link yang biasanya disebut dengan edge.
Algoritma dijkstra adalah salah satu algoritma untuk memecahkan permasalahan pencarian jarak terpendek untuk sebuah graph. Syarat graph yang dapat dicari rutenya menggunakan algoritma ini adalah graph yang berarah dengan bobot edge bernilai positif.
for each v E G.V do d [v ] =inf p M =NULL end for S = NULL Q = G.V
while Q and w [Q[l] = inf do u = ξxtract-min(Q) S=SU {u) for each v adjacent to u do if d[v] > d[u] + w[u,v] then d[v] = d[u] + w[u, v] p[v] = u DECREASE KEY[v, Q] end if end for
end while
Gambar 3 Pseudocode Algoritma Dijkstra
Gambar 3 merupakan pseudocode dari algoritma Dijkstra. Algoritma Dijkstra menggunakan strategi greedy, hal ini ditandai dengan pemilihan verteks yang selalu memilih jarak terkecil. Selanjutnya algoritma Dijkstra akan menelusuri verteks
lain melalui arah verteks tersebut, dan akan kembali ke verteks yang memiliki jarak paling kecil selanjutnya, jika jarak yang lebih kecil tidak ditemukan pada arah yang ditempuh sebelumnya (Cormen, Leiserson, Rivest, & Stein, 2001).
Untuk merepresentasikan graph, diperlukan beberapa properti. Properti umum dalam pembuatan graph adalah Node, Edge, dan weight.
Representasi rute bus Sarbagita dalam graph juga memerlukan properti graph. Node adalah halte bus Sarbagita, Edge menunjukkan hubungan antar halte, dan weight adalah bobot dari masing edge.
Tabel 1 Contoh properti graph untuk representasi rute bus Sarbagita
|
No |
NODE |
EDGE |
|
1 |
Kedonganan |
Kedonganan-> Jimbaran 1, Kedonganan->Patasari Kuta |
|
2 |
Jimbaran 1 |
Jimbaran 1-> Kedonganan, Jimbaran 1->Udayana 1 Jimbaran 1-> Taman Griya |
|
3 |
Patasari Kuta |
Patasari Kuta -> Kedonganan |
|
4 |
Taman Griya |
Taman Griya -> Mumbul Taman Griya-> Jumbaran 1 |
|
5 |
Mumbul |
Mumbul -> Taman griya |
|
6 |
Udayana 1 |
Udayana 1-> Jimbaran 1 |
Pada penelitian ini, rekomendasi rute yang akan diberikan adalah sesuai dengan rute bus sarbagita yang ada. Tidak ada kriteria lain yang digunakan dalam penentuan rute bus Sarbagita. Untuk itu, pada penelitian ini, weight yang diberikan pada masing – masing edge adalah konstan yaitu 1. Sehingga rute terpendek adalah rute dengan jumlah halte paling minimum.
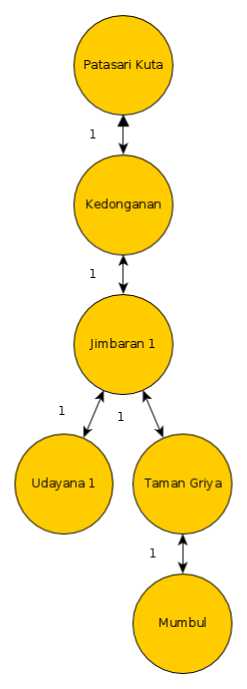
Gambar 4 Contoh representasi rute bus Sarbagita dalam graph
Karakteristik rute bus Sarbagita adalah dapat menuju dua arah, bolak – balik pada masing – masing jalur. Karakteristik graph tersebut dapat digambarkan dalam sebuah bidirectional graph atau bisa juga disebut undirected graph. Gambar 4
menunjukkan contoh representasi rute bus sarbagita menjadi sebuah graph.
Arsitektur sistem SarbagitaApps diilustrasikan pada Gambar 5.

Gambar 5 Arsitektur Sistem SarbagitaApps
Pada arsitektur sistem terdapat beberapa komponen untuk membangun aplikasi ini yaitu :
-
3.2.1. Komponen GPS Receiver
Komponen ini bertugas untuk menerima sinyal dari satelit GPS untuk menentukan lokasi aktual pengguna aplikasi. Data lokasi yang didapatkan kemudian di gunakan oleh komponen metode Haversine untuk diproses lebih lanjut.
-
3.2.2. Komponen Metode Haversine
Komponen ini berfungsi untuk mencari lokasi halte terdekat dari posisi aktual pengguna aplikasi. Dengan memanfaatkan metode Haversine, komponen ini akan menentukan lokasi halte
awal dan akhir yang diperlukan pada komponen algroitma dijkstra.
-
3.2.3. Komponen Graph Rute Sarbagita
Komponen ini bertugas sebagai database untuk menyimpan rute bus sarbagita. Data yang disimpan berupa graph. Data graph didapatkan pada saat pre-processing data. Dari data graph ini kemudian dapat dilakukan pencarian rute yang optimal.
-
3.2.4. Komponen Algoritma Dijkstra
Komponen ini bertugas untuk mencari rute yang optimal dari asal ke tujuan. Komponen ini menerima data dari komponen metode Haversine untuk mendapatkan titik halte asal dan komponen graph rute sarbagita yang menyimpan data semua rute bus sarbagita. Dari komponen ini kemudian didapatkan rute optimal dari posisi halte asal menuju ke tujuan. Rute ini kemudian dapat digunakan oleh komponen UI.
-
3.2.5. Komponen UI Sarbagita Apps
Komponen ini bertugas sebagai UI antara aplikasi dengan pengguna. Rute yang didapatkan dari komponen algoritma dijkstra kemudian di tampilkan dalam UI sehingga dapat mudah dimengerti oleh pengguna.
Aplikasi Sarbagita-Apps
merupakan aplikasi yang diharapkan dapat digunakan dalam menyediakan informasi bagi penggunanya. Informasi yang dimaksud adalah informasi mengenai rute dan lokasi dari halte bus sarbagita yang terdekat dari lokasi pengguna.
Pada penelitian ini, rute bus Sarbagita direpresentasikan dalam sebuah bidirectional graph. Dengan Node adalah halte bus, dan Edge adalah hubungan antar halte. Weight pada masing – masing edge diasumsikan konstan yaitu 1, hal ini dikarenakan penentuan rute adalah berdasarkan urutan halte yang dilalui oleh bus Sarbagita.
Aplikasi Sarbagita-Apps saat ini sedang dalam tahap pengembangan. Sesuai dengan rancangan arsitektur yang dibuat, terdapat beberapa komponen yang akan dibangun. Pada pengembangannya, Sarbagita-Apps akan menggunakan Metode Haversine untuk menentukan lokasi halte terdekat dari pengguna. Untuk mencari rute ke halte tujuan digunakan Algoritma Dijkstra.
Ardana, D., & Saputra, R. (2016).
]Penerapan Algoritma Dijkstra pada Aplikasi Pencarian Rute Bus Trans Semarang . Seminar Nasional Ilmu Komputer (SNIK 2016). Semarang: Universitas Negeri Semarang.
Bast, H., Delling, D., Goldberg, A., Muller-Hannemann, M., Pajor, T., Sanders, P. D., & Werneck, R. F. (2016). Route planning in transportation networks. In H. Bast, D. Delling, A. Goldberg, M. Muller-Hannemann, T. Pajor, P. D. Sanders, & R. F. Werneck, Algorithm Engineering.
Switzerland: Springer International Publishing.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2001). Introduction to Algorithms (Second ed.). The MIT Press.
Irawan, M. (2013). Penerapan algoritme Dijkstra pada rute angkot Bogor berbasis Android. Institut Pertanian Bogor.
Mwemezi, J. J., & Huang, Y. (2011). Optimal facility location on spherical surfaces: algorithm and
application. New York Science Journal, 21-28.
Ni, P., Vo, H. T., Dahlmeier, D. a., Ivanchev, J., & Aydt, H. (2015). Depart: Dynamic route planning in stochastic time-dependent public transit networks. 2015 IEEE 18th International Conference on Intelligent Transportation Systems (ITSC), (pp. 1672-1677). Spain.
Sofyan, A., Suryono, & Suhartono. (2012). Sistem Aplikasi Penentuan Rute Terpendek Pada Jaringan Multi Moda Transportasi Umum Menggunakan Algoritma Dijkstra. Universitas Diponegoro.
U.S. Air Force. (2017, 2 6). GPS: The Global Positioning System. Retrieved 2 11, 2017, from GPS: The Global Positioning System: http://www.gps.gov/
Discussion and feedback