PENERAPAN METODE ANT COLONY OPTIMZATION PADA METODE K-HARMONIC MEANS UNTUK KLASTERISASI DATA

Jurnal Ilmu Komputer - Volume 5 - No 1 - April 2012

PENERAPAN METODE ANT COLONY OPTIMZATION PADA METODE K-HARMONIC MEANS UNTUK KLASTERISASI DATA

I Made Kunta Wicaksana, I Made Widiartha

Jurusan Ilmu Komputer, Fakultas MIPA, Universitas Udayana, Bali

ABSTRAK

Proses pengelompokan data ke dalam beberapa klaster atau yang lebih dikenal dengan Klasterisasi Data (Data Clustering) dapat dilakukan dalam beberapa metode, salah satunya adalah metode K-Means (KM). KM adalah salah satu metode klasterisasi data yang populer karena implementasi yang sederhana, dapat menangani data dalam jumlah besar dan prosesnya yang relatif singkat. Namun Demikian KM memiliki beberapa kelemahan, diantaranya hasil klaster sensitif pada penentuan awal (inisialisasi) pusat klaster dan hasil klaster yang mengarah pada lokal optimal. Metode klasterisasi penyempurnaan dari metode KM disebut dengan K-Harmonic Means (KHM). Walaupun KHM dapat mengurangi permasalahan pada inisialisasi, namun KHM belum dapat mengatasi masalah lokal optimal. Maka dari itu diperlukan suatu metode yang memiliki solusi global.

Ant Colony Optimization (ACO) merupakan suatu algoritma semut didalam membentuk suatu koloni. Algoritma ACO dapat menghindari dari permasalahan lokal optimal dan terbukti memiliki solusi global. Dalam penelitian ini diterapkan sebuah algoritma untuk klasterisasi data yang berbasis ACO dan KHM yang disebut ACOKHM. Performa dari ACOKHM telah dibandingkan dengan algoritma ACO dan KHM dengan menggunakan lima dataset. Algoritma ACOKHM ini terbukti memiliki performa yang lebih baik dari ACO dan KHM dimana ACOKHM mampu mengoptimalkan titik pusat klaster yang mengarah ke global optimal.

Kata kunci : K-Means Clustering, K-Harmonic Means Clustering, Ant Colony Optimization, ACOKHM.

ABSTRACT

Data can be classified into several clusters, better known as Data Clustering using several methods, one of which is referred to as K-Means method (KM). It is one of the popular data clustering method. Its implementation is simple and can cope with a great number of data and the process is relatively short. However, KM has several weaknesses; the clustering result is sensitive to the initialization of the cluster center and leads to optimal local. It is the betterment of KM method referred to as K-Harmonic Means (KHM). Although it can minimize in the initialization, it could not overcome the problem of optimal local yet.

Ant Colony Optimization (ACO) is an ant algorithm used to form a colony. ACO could avoid the problem of local optimal and was proved to have global solution. In this study, an algorithm was applied to clusterizing the ACO and KHM-based data referred to as ACOKHM. The performance of ACOKHM was compared to the algorithms of ACO and KHM using five data sets. The ACOKHM algorithm was proved to have better performance than ACO and KHM, in which ACOKHM could maximize the cluster center which directs to optimal global.

Keywords: K-Means Clustering, K-Harmonic Means Clustering, Ant Colony Optimization, ACOKHM.

• 1.    Pendahuluan

Klasterisasi data merupakan bagian data mining yang bersifat tanpa arahan (unsupervised) K-Means (KM) merupakan salah satu metode klasterisasi data non hirarki yang berusaha mempartisi data yang ada ke dalam bentuk satu atau lebih klaster/kelompok. KM adalah salah satu

algoritma populer yang digunakan untuk proses partisi klasterisasi karena kelayakan dan efisiensinya pada saat berurusan dengan data yang banyak [5]. KM sangat sensitif pada inisialisasi awal, untuk mengatasi masalah yang terjadi pada inisialisasi centroid atau pusat klaster, Changhai Zhang (1999) mengusulkan sebuah

algoritma baru yang diberi nama K-Harmonic Means (KHM). Tujuan dari algoritma ini adalah meminimalisasi rata-rata harmonik dari semua titik pada data set ke seluruh pusat klaster. Meskipun algoritma KHM tidak sensitif terhadap inisialisasi, namun KHM masih belum dapat mengatasi masalah lokal optimal [5]. Ant Colony Optimization (ACO) adalah suatu algoritma yang dirancang oleh Urszula Boryczka (2008) yang diinspirasi oleh perilaku semut dalam membentuk suatu koloni [2]. Pada paper ini penulis mencoba mengekplorasi bagaimana algoritma ACO dapat membantu algoritma KHM untuk terlepas dari lokal optimal. Dengan menggunakan kedua algoritme tersebut, sebuah algoritma hibrid klasterisasi data yang disebut Ant Colony Optimization K-Harmonic Means (ACOKHM) dikenalkan oleh Hua Jiang. Berdasarkan hasil uji coba dari lima dataset didapatkan bahwa hasil dari algoritma ACOKHM lebih baik daripada KHM dan ACO [5].

Paper ini dapat dibagi menjadi 6 bagian yaitu : Bagian 1 pendahuluan, Bagian 2 memperkenalkan algoritma K-Harmonic means. Pada bagian 3 dijelaskan bagaimana algoritma ACO dipakai pada proses klasterisasi. Bagian 4 menjelaskan algoritma hibrid ACOKHM. Bagian 5 berisi implementasi dan hasil ujicoba terhadap 5 dataset, yaitu Balance Scale, Haberman, Hayesroth, Lenses, dan TAE (Teaching Assistant Evaluation). Dan bagian terakhir pada bagian 6 berisi kesimpulan.

• 2.    Metode K-Harmonic Means

K-Harmonic means merupakan salah satu metode klasterisasi data berbasis terpusat yang diperkenalkan oleh Zhang pada tahun 1999 yang kemudian dikembangkan oleh Hammerly dan Elkan pada tahun 2002. Tujuan dari algoritma ini adalah meminimalisasi rata-rata harmonik dari semua titik pada data set ke seluruh pusat klaster. Pada algoritme KHM, setiap titik data dicari jaraknya ke semua centroid. Rata-rata harmonik sensitif terhadap fakta adanya 2 atau lebih centroid yang berada dekat suatu titik data. Algoritma ini secara natural akan menukar satu atau lebih centroid ke area dimana terdapat suatu titik data yang tidak memiliki

centroid di dekatnya. Sehingga semakin baik hasil clusternya, nilai fungsi objektifnya akan semakin kecil [8].

Algoritma KHM dapat dilihat pada Gambar 2.1 dan 2.2.

Gambar 2.1 Flowchart Algoritma KHM bag.1

• 3.    Algoritma Ant Colony Optimization

Algoritma ACO diperkenalkan oleh Lumer dan Faieta (1994). Algoritma merupakan algoritma yang meniru perilaku semut mayat dan menyortir larva semut. Prinsip semut dalam mengumpulkan dan memilah larva semut ini dipakai acuan dalam algoritma ini. Algoritma ACO menyediakan partisiyang relevan dari data tanpa pengetahuan pusat klaster awal. Terdapat semut agen yang melakukan perpindahan secara acak pada grid dua dimensi dimana dalam grid tersebut terdapat objek yg tersebar secara acak, dan ukuran grid tergantung pada jumlah objek. Agen semut yang dipilih atau diizinkan untuk bergerak dalam grid, akan mengambil objek dan juga menjatuhkan

objek yang dipengaruhi oleh kesamaan dan kepadatan objek [2].

Gambar 2.2 Flowchart Algoritma KHM bag.2

Probabilitas pengambilan objek (P_pick) dari agen semut akan ditingkatkan dalam lingkungan kepadatan rendah, dan menurun jika kesamaan objek yang tinggi disekitarnya. Sebaliknya probabilitas menjatuhkan objek (P_drop) akan meningkat lingkungan kepadatan yang tinggi. Semut dan objek di grid dapat berada dalam dua situasi yaitu (a) satu semut agen memegang objek dan mengevaluasi kemungkinan menjatuhkannya pada posisi saat itu (Pdrop). (b) agen semut tanpa memegang objek bergerak dalam grid dan mengevaluasi kemungkinan mengambil suatu objek (Ppick). Akhirnya, semut agen akan mengelompokan objek berdasarkan objek yang mirip satu sama lain [2].

Fungsi probabilitas mengambil objek (P_pick) di dalam grid dan menjatuhkan objek (Pdrop) didalam grid adalah sebagai berikut :

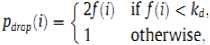
(1)

(2)

dimana :

k_p dan k_d  : nilai konstan,

f(i)        : ukuran ketetanggaan dilokasi

lingkungan tertentu π.

Rumus fungsi ukuran ketetanggan f(i) adalah

f⅛ ∑ α-¾j>) iff(o>o, f (i) = ∕   j∈Ne⅛⅛(τ)

I O                       otherwise.

(3)

dimana :

s²      : ukuran π pada lingkungan sekitar

posisi agen semut pada saat di grid.

α      : nilai konstanta yang menjelaskan

perbedaan yang mengukur d(i, j) (jarak Euclidean Distance ) antara objek i dan j [2].

Algoritma ACO dapat dilihat pada gambar

3.1

Gambar 3.1 Flowchart Algoritma ACO

• 4.    Metode ACOKHM

Metode ini merupakan hibridasi klasterisasi data antara algoritma Ant Colony Optimazition (ACO) dengan algoritma K-Harmonic Means (KHM) dan kemudian disebut dengan ACOKHM. Algoritma ini memecahkan permasalahan yang ada pada K-Harmonic Means yaitu mengatasi permasalahan lokal optima pada K-Harmonic Means. Secara garis besar algoritma ini sebagai langkahnya adalah pertama untuk penentuan inisiasi awal menggunakan algoritma ACO dan kemudian pusat klaster yang diperoleh dari algoritma ACO dijadikan pusat klaster awal pada algoritma K-Harmonic Means. Algoritma K-Harmonic Means dapat menerima inisialisasi baik dari algoritma ACO, dan memberikan masukan yang lebih baik untuk algoritma ACO pada akhirnya untuk mempercepat algoritma K-Harmonic Means (KHM) [5]. Algoritma ACOKHM dapat dilihat pada gambar 4.1 dan 4.2.

Gambar 4.1 Flowchart Algoritma ACOKHM bag 1

Gambar 4.2 Flowchart Algoritma ACOKHM bag 2.

• 5.     Pengujian

Tahapan uji coba juga akan dilakukan melalui beberapa sekenario untuk menguji performa dari metode-metode yang ada. Sekenario ini dibuat dengan menggunakan fungsi tujuan klasterisasi data yang berbeda-beda. Perbedaan fungsi tujuan ini terletak pada parameter p. Parameter p pada metode KHM merupakan parameter kunci dalam menghasilkan nilai fungsi tujuan (Yang, 2009). Hal ini menjadi dasar untuk dilakukan sekenario terhadap pemberian nilai p yang berbeda-beda.

Pada penelitian ini, terdapat tiga buah sekenario sebagai berikut:

• ■  Uji coba dengan parameter p= 2,5

• ■  Uji coba dengan parameter p= 3

• ■  Uji coba dengan parameter p= 3,5

Lima data set digunakan sebagai input untuk uji coba terhadap sistem. Data set yang digunakan adalah Balance Scale, Haberman, Hayesroth, Lenses dan TAE (Teaching Assistant Evaluation). dimana kelima dataset tersebut disimpan pada file bernama

sama dengan ekstensi data. Dataset tersebut didapatkan       dari       website       :

ftp://ftp.ics.uci.edu./pub/machine-learning-databases/. Karakteristik setiap data set dapat dilihat pada Tabel 5.1.

Tabel 5.1 Karakteristik dataset
Nama dataset	Jumlah kelas (k)	Jumlah fitur (d)	Jumlah data (n)
Balance	3	4	625
Scale
Haberman	2	3	306
Hayesroth	3	5	132
Lenses	3	4	24
TAE	3	5	151

Selain lima data set yang telah disebutkan di atas, terdapat beberapa input parameter yang dapat dilihat pada Tabel 5.2.

Tabel 5.2 Nilai parameter masukan

Parameter	Nilai
p	2,5, 3, dan 3,5
kp	0,15
kd	0,15
s	5
α	4
Gnewmax	100

Pada pengujian sistem nilai parameter p yang digunakan adalah 2,5, 3, dan 3,5. Nilai parameter k yang diinputkan tergantung dari banyak kelas dari tiap data set yang dapat dilihat pada kolom jumlah kelas (k) pada Tabel 5.1. Sedangkan nilai parameter yang lain yaitu nilai k_p , k_d, s, α, dan G_newmax sesuai yang ada pada tabel 5.2. Nilai parameter tersebut dipilih berdasarkan penelitian seleksi parameter ACO yang dilakukan oleh Hua Jiang.

Masing-masing algoritma dijalankan sebanyak 10 kali untuk setiap data set, kemudian kualitas dari hasil clustering dari ketiga algoritma dibandingkan berdasarkan : 1. Nilai fungsi tujuan KHM(X,C) yaitu hasil penjumlahan rata-rata harmonik antara titik data dengan seluruh centroid. Semakin kecil nilai KHM(X,C), semakin baik kualitas cluster tersebut.

• 2.    F-Measure adalah nilai yang didapatkan dari pengukuran precision dan recall antara class hasil cluster dengan class sebenarnya yang terdapat pada data masukan.

Precision dan recall bisa didapatkan dengan dengan

rumus sebagai berikut :

Precision (ij)^:

Recall (ij) = -ⁱ-

(4)

(5)

Sedangkan rumus untuk menghitung nilai F-Measure kelas i dengan cluster j adalah sebagai berikut :

b2.p(i.j)+r(i.j) (6)

n_i adalah jumlah data dari kelas i yang diharapkan sebagai hasil query, nj adalah jumlah data dari cluster j yang dihasilkan oleh query, dan n_ij adalah jumlah elemen dari kelas i yang masuk di cluster j. Untuk mendapatkan pembobotan yang seimbang antara precision dan recall, digunakan nilai b = 1.

Untuk mendapatkan nilai F-Measure dari dataset dengan jumlah data n, maka rumus yang digunakan adalah sebagai berikut :

F = Σ₁ -mαx_z{F(iJ)} Tl ^,

(7)

Semakin besar nilai F-Measure, semakin baik kualitas cluster tersebut [3].

Metode diimplementasikan menggunakan bahasa pemrograman Java J2SE Pada Intel Pentium Dual Core 1.73 GHz dengan RAM 1 GB. Dari hasil uji coba sistem terhadap 3 skenario yaitu parameter p = 2.5, 3, dan 3.5 didapatkan hasil Fungsi Tujuan (objective function), F-Measure, dan waktu (proses waktu yang dihabiskan untuk sebuah algoritma) dari ketiga algoritma yang dapat dilihat pada Tabel 5.3, Tabel 5.4 dan Tabel 5.5. Nilai yang dicetak tebal adalah nilai terbaik. Nilai yang di dalam kurung adalah nilai standar deviasi.

Tabel 5.3 Rata-rata dan standar deviasi dari

metode KHM, ACO dan ACOKHM dengan p =2,5.

p=2,5	KHM	ACO	ACOKH M
Balance Scale
Fs. Tujuan	330,08 (0,008)	344,658(3,40 )	329,164 (0)
F-Measure	0,476 (0)	0,449 (0,02)	0,476 (0)
Waktu	0,945 (0,014)	2,018 (0,006)	1,437(0,00 2)
Haberman
Fs. Tujuan	0,08 (0,002)	0,25 (0,014)	0,07(0,000 6)
F-Measure	0,644 (0,001)	0,573 (0,005)	0,646(0,00 1)
Waktu	0,9327 (0,002)	2,1131 (0,55)	1,414(0,00 3)
Hayesroth
Fs. Tujuan	31,144 (0,005)	32,95 (0,827)	30,25 (0)
F-Measure	0,476 (0)	0,443 (0,019)	0,479 (0)
Waktu	0,9339 (0,002)	1,826 (0,003)	1,424(0,00 2)
Lenses
Fs. Tujuan	59,911 (0,002)	61,61 (1,00)	58,768 (0)
F-Measure	0,592 (0)	0,567 (0,001)	0,599 (0)
Waktu	0,9567 (0,004)	2,133 (0,004)	1,433(0,00 2)
TAE
Fs. Tujuan	0,6334 (0,01)	0,753 (0,018)	0,542(0,00 4)
F-Measure	0,4770 (0)	0,447 (0,011)	0,477(0,00 4)
Waktu	0,9062 (0,002)	1,828 (0,004)	1,381 (0,01)

Tabel 5.4 Rata-rata dan standar deviasi dari

metode KHM, ACO dan ACOKHM dengan p =3.

p=3      ∖	KHM ∖	ACO ∖	ACOKHM
Balance Scale
Fs. Tujuan	505,51 (0,03)	512,5 (0,23)	503,35 (0)
F-Measure	0,541 (0)	0,427(0,00 1)	0,541 (0)
Waktu	0,916 (0,011)	2,083 (0,03)	1,388(0,01 4)
Haberman
Fs. Tujuan	0,02 (0,018)	0,14 (0,007)	0,01(0,000 4)
F-Measure	0,730 (0,0006)	0,83 (0,002)	0,7269(0,0 1)
Waktu	0,94 (0,002)	1,93 (0,05)	1,40 (0,001)
Hayesroth
Fs. Tujuan	26,48 (0,002)	27,69 (0,42)	25,37 (0)

F-Measure	0,4223 (0)	0,422(0,00 4)	0,454 (0)
Waktu	0,906 (0,003)	1,98 (0,056)	1,421(0,00 2)
Lenses
Fs. Tujuan	67,76 (0,007)	68,85 (0,52)	66,34 (0)
F-Measure	0,472 (0)	0,46 (0,002)	0,472 (0)
Waktu	0,912 (0,002)	2,09 (0,27)	1,413(0,00 3)
TAE
Fs. Tujuan	0,208 (0,0009)	0,55 (0,01)	0,134 (0)
F-Measure	0,474 (0)	0,453(0,00 2)	0,474 (0)
Waktu	0,90 (0,002)	1,8 (0,005)	1,393(0,00 2)

Tabel 5.5 Rata-rata dan standar deviasi dari

metode KHM, ACO dan ACOKHM dengan p =2,5.

p=3	KHM	ACO	ACOKH M
Balance Scale
Fs. Tujuan	830,69 (0,003)	844,07 (0,5)	829,73 (0)
F- Measure	0,534 (0)	0,513 (0,003)	0,534 (0)
Waktu	0,9377 (0,001)	1,792 (0,02)	1,42 (0,001)
Haberman
Fs. Tujuan	0,003 (0,001)	0,02 (0,001)	0,001 (0)
F- Measure	0,689 (0)	0,674 (0,003)	0,689 (0)
Waktu	1,045 (0,003)	1,863 (0,003)	1,49 (0,003)
Hayesroth
Fs. Tujuan	25,7548 (0,008)	27,73 (0,27)	25,45 (0)
F- Measure	0,455 (0)	0,424 (0,003)	0,455 (0)
Waktu	0,9358 (0,004)	1,976 (0,01)	1,42 (0,004)
Lenses
Fs. Tujuan	60,4804 (0,004)	61,814 (0,46)	59,323 (0)
F- Measure	0,523 (0)	0,421 (0,002)	0,523 (0)
Waktu	0,9288 (0,002)	2,0003(0,005 )	1,417 (0004)
TAE
Fs. Tujuan	0,0737 (0,004)	0,0737 (0,03)	0,053 (0)
F- Measure	0,4810 (0)	0,426 (0,007)	0,481 (0)
Waktu	0,9461 (0,0022)	1,839 (0,003)	1,42 (0,002)

• a)     Pada Tabel 5.3, dari lima dataset

yang diujicobakan dengan parameter p= 2,5 dengan percobaan yang dilakukan sepuluh kali, menunjukan metode ACOKHM memiliki performa yang terbaik. Dengan nilai fungsi tujuan yang terkecil dan F-measure yang terbesar.

• b)     Pada Tabel 5.4, percobaan yang

dilakukan dalam sepuluh kali dengan parameter p = 3, terlihat dari lima dataset, ACOKHM memiliki performa yang paling bagus. Dengan nilai fungsi tujuan yang kecil dan nilai F-Measure yang besar. Kecuali pada dataset Haberman dengan nilai F-Measure yang terbesar ada pada metode ACO.

• c)     Pada percobaan dengan parameter p

= 3,5 sebanyak sepuluh kali pada setiap dataset, metode ACOKHM memiliki performa yang paling bagus dari pada kedua metode pembanding yaitu ACO dan KHM.

• 6.    Kesimpulan

berdasarkan hasil rangkaian uji coba dan analisa penelitian yang dilakukan dapat diambil beberapa kesimpulan sebagai berikut

• 1.    Dalam metode ACOKHM, posisi titik pusat klaster telah berhasil dioptimalkan dengan mengarahkan hasil klaster menuju solusi global optimum. Hal ini dapat dibuktikan dengan hasil penelitian yang menunjukkan nilai fungsi tujuan (objective   function)   dari metode

ACOKHM merupakan yang terkecil dari kedua metode pembanding yang digunakan yaitu KHM dan ACO.

• 2.    Pada nilai F-Measure yaitu nilai yang didapat dari pengukuran hasil klaster secara eksternal (kelas label), metode ACOKHM memperoleh nilai terbesar dari kedua metode lainnya. Dari lima belas hasil rekapan uji coba (kombinasi tiga parameter p dan lima dataset), hanya terdapat satu nilai F-Measure dari metode ACOKHM yang lebih rendah dari nilai yang dihasilkan dari metode pembanding.

• 3.    Dari hasil waktu yang dibutuhkan untuk melakukan proses klasterisasi data, metode ACOKHM membutuhkan waktu yang lebih lama jika dibandingkan dengan metode KHM, tetapi ACOKHM

membutuhkan waktu yang lebih singkat daripada metode ACO.

Daftar Pustaka

• [1]    Anil, K.Jain.2010. Data clustering: 50 years beyond K-means. Michigan : Michigan State University.

• [2]    Boryczka, Urszula. 2008. Ant Clustering Algorithm. Poland : Institute of Computer Science University of Silesia.

• [3]    Dalli, Angelo. 2002. Adaptation of the F-Measure to Cluster Based Lexicon Quality Evaluation. England : University of Sheffild.

• [4]    Gungor, Zulal. 2007. K-Harmonic Means Data Clustering With Simulated Annealing Heuristic. Turkey : Gazi University Engineering Faculty.

• [5]    Jiang, Hua. 2010. Ant Clustering Algorithm with K-Harmonic Means Clustering. China : Northeast Normal University.

• [6]    Sclove, Stanley L. 2001. Statistics for Information Systems and Data Mining. Chicago : University of Illinois.

• [7]    Yang, Fengqin. 2010. An efficient hybrid data clustering method based on K-harmonic means and Particle Swarm Optimization. China : Northeast Normal University, Changchun, Jilin

• [8]    Zhang, Bin. 1999. K-Harmonic Means - A Data Clustering Algorithm. HP Laboratories Palo Alto.

[Halaman ini sengaja dikosongkan]

62