How Big Poverty in Central Java: Mixed Regressive-Spatial Autoregressive Models
on
pISSN : 2301 - 8968
eISSN : 2303 - 0186
JEKT ♦ 11 [1] : 53-60
Analisis Kemiskinan Di Provinsi Jawa Tengah Dengan Pendekatan Spatial Autoregressive Model
Rezzy Eko Caraka*
Departement of Statistics Diponegoro University
ABSTRACT
Spatial Autoregressive Model (SAR) is also called Spatial Lag Model (SLM) is one area of spatial models approach taking into account the spatial lag effect on the dependent variables. Testing spatial effect is made to see if a variable has an influence on the spatial location. In these discussions, the model used Spatial Autoregressive (SAR) to identify and analyze the factors that affect the category of poor people in Central Java. Retrieved 3 variables were significant at α = 10 %, i.e. the GDP of Central Java in 2010, the population in Central Java in 2010 who did not finish primary and primary schooling, the number of people in Central Java in 2010 who graduated from high school.
Keywords: SAR;Spatial; Poverty; East Java
ABSTRAK
Spatial Autoregressive Model (SAR) disebut juga Spatial Lag Model (SLM) adalah salah satu model spasial dengan pendekatan area dengan memperhitungkan pengaruh spasial lag pada variabel dependen. Pengujian efek spasial dilakukan untuk melihat apakah variabel memiliki pengaruh spasial di suatu lokasi. Pada pembahasan ini digunakan model Spatial Autoregressive (SAR) untuk menentukan dan menganalisis faktor-faktor yang mempengaruhi kategori penduduk miskin di Jawa Tengah. Diperoleh 3 variabel yang signifikan pada α = 10% yaitu PDRB Jawa Tengah tahun 2010, jumlah penduduk di Jawa Tengah tahun 2010 yang tidak tamat SD dan tamat SD, jumlah penduduk di Jawa Tengah tahun 2010 yang tamat SMA.
Kata kunci: SAR; Spatial; Kemiskinan; Jawa Tengah
PENDAHULUAN
Permasalahan ekonomi sering kali menjadi hal yang akan selalu ada di belahan bumi manapun termasuk Indonesia yaitu kemiskinan. Kemiskinan tentunya akan berpengaruh pada sektor pendidikan, semakin tinggi angka kemiskinan artinya akan lebih banyak anak yang putus sekolah dengan alasan tidak punya biaya untuk sekolah. Padahal selama ini diketahui bahwa pendidikan itu penting untuk membangun sumber daya manusia yang handal. Tanpa
sumber daya manusia yang handal maka sebuah negara akan sulit berkembang.
Masalah kemiskinan di Jawa Tengah masih menjadi beban pemerintah dalam menyejahterakan masyarakat. Menurut Kepala Bidang Statistik Sosial BPS Jawa Tengah jumlah penduduk miskin di Jawa Tengah pada tahun 2010 yaitu 5,369 juta orang dengan persentase sebesar 57,93% penduduk miskin berada di wilayah perdesaan dan oleh pemerintah pusat penduduk di Jawa Tengah masih tergolong penduduk miskin. Penentuan
53
suatu wilayah tergolong miskin berdasarkan pada faktor-faktor yang berpengaruh dalam masalah kemiskinan dan menggunakan analisis yang biasanya masih bersifat umum, misalnya analisis regresi yang hanya mampu memberikan informasi yang tepat jika wilayah penelitian kecil, penduduk bersifat homogen, dan antar wilayah diasumsikan independen atau saling tidak mempengaruhi. Akan tetapi, kondisi kemiskinan suatu wilayah sangat mungkin dipengaruhi oleh lokasi pengamatan atau kondisi geografis wilayah, termasuk posisinya terhadap wilayah lain di sekitarnya. Jika model regresi klasik digunakan sebagai alat analisis pada data spasial, maka bisa menyebabkan kesimpulan yang kurang tepat karena unsur spasial tidak tercakup didalamnya sehingga model regresi spasial diharapkan mampu untuk menentukan dan menganalisis faktor-faktor yang mempengaruhi kategori penduduk miskin di Jawa Tengah sehingga hasilnya dapat digunakan sebagai sumber referensi yang lebih tepat dalam pengentasan kemiskinan di Jawa Tengah. Untuk menentukan faktor-faktor yang berpengaruh terhadap kemiskinan, penelitian ini menggunakan model regresi spasial yaitu Spatial Autoregressive (SAR).
KAJIAN TEORITIS DAN PENGEMBANGAN HIPOTESIS
Regresi Ordinary Least Square
Persamaan regresi linear yang biasa didefinisikan dengan menggunakan metode pendugaan parameter Ordinary Least Square (OLS), secara umum dapat dituliskan:
k
Z= β0 +∑ βjxi + εi
j=1
Vektor galat ε diasumsikan menyebar N (0, σ2)
Keterangan :
i : variabel respon pada
pengamatan ke-i (i = 1,2,…,n)
0 : konstanta
j : parameter regresi ke- j(j =
-
1,2, ...,k)
ij : variabel prediktor ke- j pada
pengamatan ke -i
: residual dengan asumsi identik,
independen, dan berdisribusi
normal dengan mean nol dan varians σ2
n : banyaknya amatan atau lokasi
(k+1)
Dalam bentuk matriks dapat diuraikan sebagai berikut :
y=Xβ+ ε
(2)

dimana :
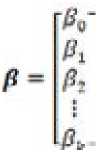
Spatial Autoregressive Model (SAR)
Dalam permodelan, apabila model regresi klasik digunakan sebagai alat analisis pada data spasial, dapat menyebabkan kesimpulan yang kurang tepat karena asumsi residual saling bebas dan asumsi homogenitas tidak terpenuhi.
Menurut(Anselin, 1998) model umum regresi spasial dinyatakan dengan :
y = ρW1y + Xβ + u (3)
u = λW2u + ε (4)
ε ~ N(0, σ2I)
dengan
y : Vektor variabel dependen, ukuran n x 1
X : matriks variabel independen, ukuran n x (k+1)
β : Vektor parameter koefisien regresi, berukuran (k+1) x 1
ρ : Parameter koefisien spasial lag variabel dependen
λ : Parameter koefisien spasial lag pada residual
u : Vektor residual pada persamaan (4) berukuran n x 1
ε : Vektor residual pada persamaan (4) berukuran n x 1, yang berdistribusi normal dengan mean nol dan varians σ2I
W1,W2 : Matriks pembobot, berukuran n x n
I : Matriks Identitas, berukuran n x n n : Banyaknya amatan/lokasi (i = 1,2,…, n) k : Banyaknya variabel independen.
Residual regresi (u) yang diasumsikan memiliki efek lokasi random dan mempunyai autokorelasi secara spasial. W1dan W2 merupakan pembobot yang menunjukkan hubungan contiguity antar lokasi dan diagonalnya bernilai nol.
Ada beberapa model yang bisa dibentuk dari model umum regresi spasial ini, yaitu:
-
(i) Apabila ρ = 0 dan λ = 0, maka persamaan
menjadi
Y = Xβ + ε
Persamaan ini disebut model regresi klasik atau lazim dikenal sebagai model regresi Ordinary Least Square (OLS), yaitu regresi yang tidak mempunyai efek spasial.
-
(ii) Jika nilai W2 = 0 atau λ = 0 maka akan menjadi model regresi spasial Mixed Regressive-Autoregressive atau Spatial Autoregressive Model (SAR)
y = ρW1y + Xβ + ε (5)
ε ~ N(0, σ2I)
Model ini mengasumsikan bahwa proses autoregressive hanya pada variabel dependen (iii) Jika nilai W1 = 0 atau ρ = 0 maka akan menjadi model Spatial Residual Model (SEM) seperti pada persamaan (6)
y = Xβ + λW2u + ε (6)
ε ~ N(0, σ2I)
λW2u menunjukkan spasial struktur λW2 pada spatially dependent residual (ε)
(iv) Nilai W1,W2 ≠ 0, λ ≠ 0 atau ρ ≠ 0 maka disebut Spatial Autoregressive Moving Average (SARMA)
Spatial Autoregressive Model (SAR) disebut juga Spatial Lag Model (SLM) adalah salah satu model spasial dengan pendekatan area dengan memperhitungkan pengaruh spasial lag pada variabel dependen saja. Model ini dinamakan juga Mixed Regressive-Autoregressive karena mengkombinasikan model regresi biasa dengan model regresi spasial lag pada variabel dependen (Anselin, 1988). Variasi dalam y sebagai kombinasi
linear dari unit yang berdekatan tanpa variabel independen.
Penaksiran parameter pada model autoregressive spatialmenggunakan metode penaksiran maximumlikelihood dimana parameter-parameter yang belum diketahui diperoleh dengan memaksimumkan suatu fungsi kemungkinan (likelihood function).
Menurut Anselin (1988) model autoregresif regresi spasial campuran mempunyai fungsi log-likelihood seperti berikut
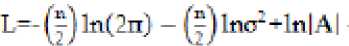
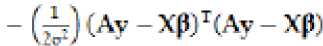
DimanaA= I-ρW
Sedangkan untuk penaksir parameter dan σ2adalah sebagai berikut:
b = bo - ρbL ...(8)
...(9)
Kemudian persamaan (8) dan (9) disubstitusikan ke dalam persamaan (7) sehingga diperoleh fungsi log-likelihood concentrated seperti berikut:
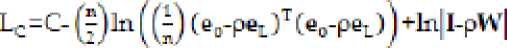
...(10)
dimana C adalah konstanta. Fungsi (10) merupakan fungsi nonlinier dalam satu parameter yaitu , dan dapat dimaksimumkan menggunakan teknik numerik dengan pencarian langsung.
Untuk lebih jelasnya Anselin (1988) telah menjelaskan langkah-langkah penaksiran parameter model sebagai berikut:
Melakukan penaksiran dengan menggunakan metode kuadrat terkecil biasa untuk model:
y = Xb0+e0 (11)
dimana
b0 = (XTX)-1XTy (12)
Melakukan penaksiran dengan menggunakan metode kuadrat terkecil biasa untuk model:
Wy = XbL + eL (13)
dimana
bL = (XTX)-1XTWy (14)
Setelah b0 dan bL diperoleh, hitung nilai residu dengan menggunakan persamaan sebagai berikut:
e0 = y – Xb0 (15)
eL = Wy–XbL (16)
Setelah diperoleh b0, bL, e0 dan eL, substitusikan persamaan (8) dan (9) ke dalam persamaan (7) sehingga dihasilkan fungsi log-likelihood concentrated seperti pada persamaan (10).
Selanjutnyacariyangmemaksimumkan persamaan (10) dengan menggunakan teknik numerik.
Setelah diperoleh, hitung:
b □ = b0 - ρbL
(17)
danσ □2 = (1∕n)( e0 - ρeL)T( e0 - ρeL)
(18)
Moran’s I
Koefisien Moran’s I digunakan untuk uji dependensi spasial atau autokorelasi antar amatan atau lokasi. [3]
Hipotesis yang digunakan adalah :
Ho : I = 0 (tidak ada autokorelasi antar lokasi) H1 : I ≠ 0 (ada autokorelasi antar lokasi) Statistik Uji :
Zhitung= (I-I0)/√(Var(I))
= Λ∑^i∑^1<^^^
Dimana IMs=
^ Ejl1 [“-'J
S0= Σ⅛; Σ⅛ W
E(IMs)=I0= ⅛
Var(IMs)=
⅞⅛g - 3?! +⅜ -W?- -2 ⅛] ⅛Kg2⅛kZ⅛jj⅞l _^]_ (n-l)⅛-≈)(t-3)sj (⅛-t×u-2×-a-3)sJ K-I
k= ∑⅛ + ^2
Dengan xi adalah data ke-i, xj data ke-j, x □ rata-rata data, var (I) varians Moran’s I, dan E(I) expected value. Pengambilan keputusan Ho ditolak jika |Zhitung|>Zα/2. Nilai dari indeks I adalah antara -1 dan 1. Apabila I > Io maka data memiliki autokorelasi positif, jika I < Io maka data memiliki autokorelasi negatif.
Pola pengelompokan dan penyebaran antar lokasi dapat juga disajikan dengan Moran’s Scatterplot yang menunjukkan hubungan antara nilai amatan pada suatu lokasi (distandarisasi) dengan rata-rata nilai amatan dari lokasi-lokasi yang bertetanggaan dengan lokasi yang bersangkutan.[4] Scatterplot tersebut terdiri atas empat kuadran, yaitu kuadran I, II, III, dan IV. Lokasi-lokasi yang banyak berada di kuadran I dan III cenderung memiliki autokorelasi positif. Sedangkan lokasi-lokasi yang banyak berada di kuadran II dan IV cenderung memiliki autokorelasi negatif. Berikut penjelasan dari masing-masing kuadran (Perobelli dan Haddad, 2003).
Kuadran I (High-High), menunjukkan lokasi yang mempunyai nilai amatan tinggi dikelilingi oleh lokasi yang mempunyai nilai amatan tinggi.
Kuadran II (Low-High), menunjukkan lokasi yang mempunyai nilai amatan rendah dikelilingi oleh lokasi yang mempunyai nilai amatan tinggi.
Kuadran III (Low-Low), menunjukkan lokasi yang mempunyai nilai amatan rendah dikelilingi oleh lokasi yang mempunyai nilai amatan rendah.
Kuadran IV (High-Low), menunjukkan lokasi yang mempunyai nilai amatan tinggi dikelilingi oleh lokasi yang mempunyai nilai amatan rendah.
HASIL DAN PEMBAHASAN
Sumber utama data penelitian ini diambil dari hasil Susenas yang dilaksanakan oleh Badan Pusat Statistik Provinsi Jawa Tengah. Data diperoleh dengan menggunakan metode dokumentasi. Pengumpulan data dimulai dengan tahap penelitian pendahuluan yaitu melakukan studi kepustakaan dengan mempelajari buku-buku dan bacaan-bacaan lain yang berhubungan dengan pokok bahasan dalam penelitian ini. Pada tahap ini juga dilakukan pengkajian data yang dibutuhkan, yaitu mengenai jenis data yang dibutuhkan, ketersediaan data, dan gambaran cara pengolahan data. Tahapan selanjutnya adalah penelitian pokok yang digunakan untuk mengumpulkan keseluruhan data
|
Peubah |
Koefisien |
Galat Baku |
Nilai p-value |
|
Konstanta |
294770,6 |
159241,4 |
0,0743655 |
|
UMK |
-0,407636 |
0,2130423 |
0,0656147 |
|
PDRB |
-0,001305183 |
0,003126365 |
0,6794043 |
|
TSD |
0,5573015 |
0,1162182 |
0,0000448 |
|
TSMP |
-0,359573 |
0,4856976 |
0,4650564 |
|
TSMA |
0,4281279 |
0,2291641 |
0,0718660 |
|
Peubah |
Koefisien |
Galat Baku |
Nilai p-val-ue |
|
Konstanta |
326947,6 |
149633,9 |
0,0365723 |
|
UMK |
-0,4541823 |
0,1998278 |
0,0301171 |
|
TSD |
0,4836112 |
0,06806683 |
0,0000001 |
|
TSMA |
0,2836418 |
0,1411401 |
0,0532415 |
yang dibutuhkan guna menjawab persoalan penelitian dan memperkaya literatur untuk menunjang data kuantitatif yang diperoleh.
-
3.1 Regresi OLS
Persamaan yang diperoleh adalah sebagai berikut :
Y = 294770,6 – 0,407636 X1 – 0,001305183 X2 + 0,5573015 X3 – 0,359573 X4 + 0,4281279 X5 dimana :
-
X1 = Upah Minimum Tenaga Kerja di Jawa Tengah tahun 2010 (UMK)
X2 = PDRB Jawa Tengah tahun 2010 (PDRB)
X3 = Jumlah penduduk di Jawa Tengah tahun 2010 yang tidak tamat SD dan tamat SD (TSD)
X4 = Jumlah penduduk di Jawa Tengah tahun 2010 yang tamat SMP (TSMP)
X5 = Jumlah penduduk di Jawa Tengah tahun 2010 yang tamat SMA (TSMA)
Pengujian signifikansi parameter dilihat pada tabel dibawah ini dengan rumusan hipotesis:
H0 : Parameter tidak signifikan
H1 : Parameter signifikan
Dari Tabel 1 didapatkan bahwa koefisien parameter untuk upah minimum tenaga kerja (X1) dengan p-value sebesar 0,0656147 <0,1
(α), sehingga koefisien parameter untuk upah minimum tenaga kerja (X1) signifikan, yang berarti bahwa ada pengaruh Upah Minimum Tenaga Kerja terhadap jumlah penduduk miskin di Jawa Tengah pada tahun 2010, begitu pula untuk parameter jumlah penduduk yang tidak tamat SD dan tamat SD ( X3) dan jumlah penduduk yang tamat SMA (X5).
Sehingga didapatkan Model akhir OLS setelah dilakukan regresi kembali dengan variabel-variabelnya yang mempengaruhi jumlah penduduk miskin di Jawa Tengah pada tahun 2010 pada Tabel 1
R-square = 0,811830
Keterangan: *) taraf nyata pada α = 10% Persamaan Model Regresi OLS akhir = Y = 326947,6 – 0,4541823 X1 + 0,4836112 X3 + 0,2836418 X5
-
3.2 Regresi Spasial
Pengujian spasial dependence menggunakan statistik Moran’s I. Pada pengujian ini diperlukan matriks pembobot yang merupakan hal terpenting dalam autokorelasi spasial. Gambar di bawah ini merupakan diagram Moran’s I untuk Jumlah Penduduk Miskin di Jawa Tengah pada tahun 2010.
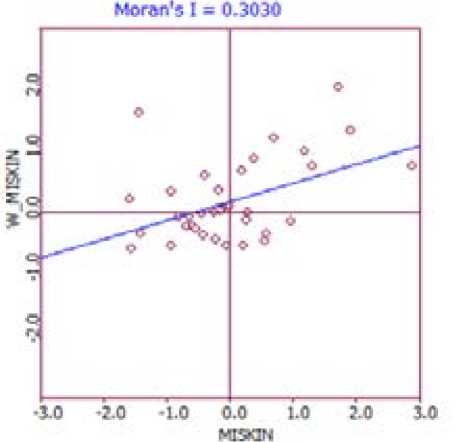
Pada gambar 1 pola data menyebar di kuadran I dan III, sehingga didapatkan bahwa Kota/Kabupaten dengan nilai pengamatan tinggi dikelilingi oleh daerah dengan nilai pengamatan yang tinggi pula dan Kota/ Kabupaten dengan nilai pengamatan rendah dikelilingi oleh daerah dengan nilai pengamatan yang rendah pula. Hal ini membuat autokorelasi yang terjadi cenderung positif. Sehingga Jumlah Penduduk Miskin di Jawa Tengah tahun 2010, pada tiap kabupaten/kota dengan jumlah penduduk miskin rendah, maka akan dikelilingi oleh jumlah penduduk miskin yang rendah pula dan begitu juga sebaliknya.
Indeks Moran’s I yang dihasilkan dari Jumlah Penduduk Miskin di Jawa Tengah tahun 2010 adalah I=0,3030, atau p-value sama dengan 0,005 ( < α = 0.05). Maka dapat disimpulkan bahwa terdapat autokorelasi spasial pada Jumlah Penduduk Miskin di Jawa Tengah tahun 2011 sehingga digunakan regresi spasial.
-
3.2 Model Regresi SAR
Persamaan yang diperoleh adalah sebagai berikut :
Y = 35664,77 + 0,304339 Wu – 0,1207127 X1 – 0.004688208 X2 + 0.5648048 X3 – 0.2627854 X4 + 0,4479426 X5 dimana :
-
X1 = Upah Minimum Tenaga Kerja
di Jawa Tengah tahun 2010 (UMK)
X2 = PDRB Jawa Tengah tahun 2010 (PDRB)
X3 = Jumlah penduduk di Jawa Tengah tahun 2010 yang tidak tamat SD dan tamat SD (TSD)
X4 = Jumlah penduduk di Jawa Tengah tahun 2010 yang tamat SMP (TSMP)
X5 = Jumlah penduduk di Jawa Tengah tahun 2010 yang tamat SMA (TSMA)
Pengujian signifikansi parameter dilihat pada tabel dibawah ini dengan rumusan hipotesis:
H0 : Parameter tidak signifikan
H1 : Parameter signifikan
Keterangan: *) taraf nyata pada α = 10%
Dari tabel diatas didapatkan bahwa koefisien parameter untuk rho (ρ) dengan p-value sebesar 0,0185839 <0,1 (α), sehingga koefisien parameter untuk rho (ρ) signifikan, yang berarti bahwa terdapat pengaruh spasial atau lokasi yang berdekatan, berpengaruh terhadap pengamatan yaitu jumlah penduduk miskin di Jawa Tengah pada tahun 2010, begitu pula untuk koefisien parameter PDRB (X2), jumlah penduduk yang tidak tamat SD dan tamat SD ( X3) dan jumlah penduduk yang tamat SMA (X5). Sehingga didapatkan Model akhir dengan menggunakan metode SAR setelah dilakukan regresi kembali dengan variabel-variabelnya yang mempengaruhi jumlah penduduk miskin di Jawa Tengah pada tahun 2010 pada Tabel 4.
Keterangan: *) taraf nyata pada α = 10% Persamaan yang diperoleh adalah sebagai berikut :
Y = – 64602,97 + 0,357966 Wu – 0,005549373 X2 + 0.5394153 X3 + 0,3563087 X5
-
3.2.1 Uji Asumsi Model SAR
Pengujian asumsi pada model regresi spasial adalah uji homoskedastisitas atau uji kehomogenan dan uji sisaan berdistribusi normal atau uji kenormalan. Pengujian asumsi dilakukan pada setiap model regresi spasial yang terbentuk.
-
a. Uji Kehomogenan Residual
Pada pengujian kehomogenan ragam dapat dilakukan dilakukan dengan uji Breusch Pagan (BP Test) dengan hipotesisnya adalah sebagai berikut:
Ho = Ragam residual homogen
H1 = Ragam Residual tidak homogen
Taraf signifikansi = α : 5%
Berdasarkan tabel 5, didapatkan nilai BP test adalah 3,263253 <7.81 (X2 (5%,3)) atau p-value sebesar 0,3527899 (>α 0,05), sehingga Ho diterima. Maka, Ragam dari residual pada model SAR adalah homogen. Jadi, asumsi homogenitas residual/homoskedastisitas terpenuhi.
-
b. Uji Kenormalan Residual
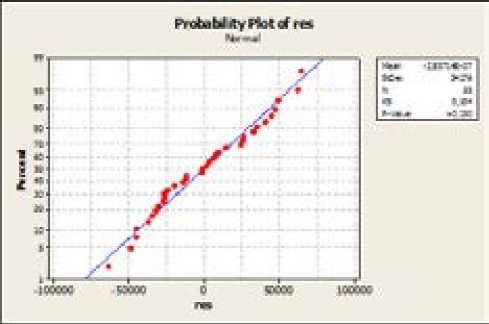
Pada pengujian kenormalan residual dapat dilakukan dengan mengunakan uji Kolmogorov-Smirnov (KS Test). Hipotesis yang digunakan adalah Ho = Residual berdistribusi normal, H1 = Residual idak berdistribusi normal. Gambar dibawah ini merupakan gambar Probability Plot untuk Residual dari Model SAR.
Berdasarkan Gambar 2 diatas, maka didapatkan nilai Kolmogorov Smirnov (KS) sebesar 0,104 dengan p-value sebesar (>0,150) > 0,05 (α). Sehingga Ho diterima, maka residual dari model SAR tersebut berdistribusi normal. Jadi, asumsi normalitas terpenuhi.
Model regresi yang terbentuk pada Jumlah penduduk Miskin di Jawa Tengah menggunakan Model Spasial Autoregressive
adalah:
Yi = – 64602,97 + 0,357966 Wu – 0,005549373 X2 + 0.5394153 X3 + 0,3563087 X5
Koefisien variabel PDRB sebesar – 0,005549373, nilai ini menunjukkan bahwa setiap penurunan PDRB sebesar satu satuan akan menambah jumlah penduduk miskin di Jawa Tengah tahun 2010 sebesar 0,005549373, dengan asumsi faktor lain dianggap konstan. Koefisien variabel jumlah penduduk di Jawa Tengah yang tidak tamat SD dan tamat SD sebesar 0.5394153 menunjukkan bahwa setiap kenaikan penduduk di Jawa Tengah yang tidak tamat SD dan tamat SD sebesar satu-satuan akan mengurangi jumlah penduduk miskin di Jawa Tengah tahun 2010 sebesar 0.5394153, dengan asumsi faktor lain dianggap konstan. Koefisien variabel jumlah penduduk di Jawa Tengah yang tamat SMA sebesar 0,3563087 menunjukkan bahwa setiap penambahan jumlah penduduk di Jawa Tengah yang tamat SMA sebesar satu-satuan akan mengurangi jumlah penduduk miskin di Jawa Tengah tahun 2010 sebesar 0,3563087, dengan asumsi faktor lain dianggap konstan. Tabel 5.Perbandingan Model regresi Klasik OLS dan Model SAR
Berdasarkan kriteria MSE dan R2 nya, maka dapat dikatakan bahwa model SAR lebih baik karena nilai MSE nya terkecil dan nilai R-Square besar.
KESIMPULAN
Pemodelan regresi dengan menggunakan metode Ordinary Least Square (OLS) menghasilkan sebagian kecil parameter tidak signifikan pengaruhnya terhadap jumlah penduduk miskin di Jawa Tengah pada tahun 2010 pada taraf α = 10%. Pemodelan regresi dengan menggunakan metode SAR menunjukkan bahwa lag variable dependen berperan penting pada pemodelan jumlah penduduk miskin di Jawa Tengah pada tahun 2010. Sedangkan untuk factor-faktor eksternal yang mempengaruhi jumlah miskin penduduk didapatkan bahwa dari 5 variabel bebas, ada 3 variabel yang signifikan pada α = 10% yaitu PDRB Jawa Tengah tahun 2010 (PDRB/X2), jumlah penduduk di Jawa Tengah tahun 2010 yang tidak tamat SD
dan tamat SD (TSD/X3), jumlah penduduk di Jawa Tengah tahun 2010 yang tamat SMA (TSMA/X5). Kemudian pemilihan model terbaik didapatkan model SAR lebih baik dibandingkan model regresi dengan metode OLS dengan R2=81,1830% dan MSE=36930 sedangkan metode SAR diperoleh nilai R2=84,1669% dan MSE=33903,1. Sehingga model SAR yang didapat adalah
Y = – 64602,97 + 0,357966 Wu – 0,005549373 X2 + 0.5394153 X3 + 0,3563087 X5
DAFTAR PUSTAKA
Anselin, L. 1988. Spatial Econometrics : Methods and Models.Dordrecht: Kluwer Academic Publishers
Ad Dien ,Hisyam. 2011. Penduduk Miskin di Jateng. www.Republika.co.id.
Arbia, G. 2006.Spatial Econometrics. Berlin: Springer-Verlag
Arisanti, R. 2011. Model Regresi Spasial untuk Deteksi Faktor-Faktor Kemiskinan di Provinsi Jawa Timur [Tesis]. Bogor: Fakultas Matematika dan Ilmu Pengetahuan Alam IPB. Choiriyah, N.I. 2009. Karakterisitik Siswa Putus Sekolah Tingkat SD dan SMP di Kawasan Surabaya Utara. [Tugas Akhir]. Surabaya: Program Sarjana Jurusan Statistika ITS.
Draper N.R., Smith H. 1992. Analisis Regresi Terapan. Edisi ke-2. Sumantri B, Penerjemah. Jakarta: Gramedia Pustaka Utama. Terjemahan dari : Applied Regression Analysis
Gujarati., Z. 1978. Ekonometrika Dasar alih bahasa dari Basic Econometrics. Jakarta: Erlangga
Lee J.and Wong D.W.S. 2001, Statistic for Spatial Data, John Wiley & Sons, Inc, New York.
LeSage, J.P. 1999. Spatial Econometrics. Toledo: Department of Economics University of Toledo.
Sembiring, R.K. 2003. Analisis Regresi (Edisi Kedua). Bandung: Penerbit ITB
Wei, W.W. 1990. Time Series Analysis. Addison-Wesley Publishing Company.
60
Discussion and feedback