Beta Convergence and Sigma Convergence: Evidence from Indonesian District-Level Data

plSSΝ : 2301 - 8968

elSSΝ : 2303 -0186

JEΚT^10 [1] : 19-25

Beta Convergence and Sigma Convergence: Evidence from Indonesian District-Level Data

Nenny Hendajany*

Didin Saepudin Ae Suaesih

Universitas Sangga Buana

ABSTRACT

In this paper, we describe three things, (1) Evidence of β-convergence’s existence in Indonesian districts-level data, (2) the reason of why σ-convergence may not accompany β-convergence, and (3) the demonstration to show that σ-convergence cannot be detected at the districts level across Indonesia using Indonesian districts -level data that contains over 277 cross-sectional observations. If Indonesian individual provinces are considered separately, we find only 2 out of 25 provinces with detected σ-convergence. But also, in many cases statistically significant σ-divergence is found.

Keywords: β-convergence, σ-convergence and speed of convergence

Konvergensi Beta dan Konvergensi Sigma: Bukti dari data Tingkat Kabupaten di Indonesia

ABSTRAK

Dalam tulisan ini, kami menjelaskan tiga hal, (1) Bukti keberadaan β-konvergensi dalam Data tingkat kabupaten di Indonesia, (2) alasan mengapa σ-konvergensi mungkin terjadi tanpa adanya β-konvergensi, dan (3) gambaran untuk menunjukkan bahwa σ-konvergensi tidak dapat dideteksi di tingkat kabupaten di seluruh Indonesia dengan menggunakan data tingkat kabupaten di Indonesia, yang berisi lebih dari 277 observasi cross-sectional. Jika masing-masing propinsi Indonesia dianggap secara terpisah, kita dapat menemukan hanya 2 dari 25 provinsi yang memiliki σ-konvergensi. Akan tetapi, dalam banyak kasus juga ditemukan adanya σ-divergensi yang signifikan secara statistik.

Kata kunci: beta-konvergensi, σ-konvergensi dan kecepatan konvergensi

INTRODUCTION

One of the goals of economic development is equitable. The tendency of poor countries or regions to grow faster than rich ones has been quite basic of all economic issues: are there automatic forces that lead to the convergence over time in the levels of per capita income and product?

One can differentiate the convergence ingrowth empirics as two types: σ-convergence and β-convergence. When the dispersion of real per capita income (hereafter, simply “income” across a group of economies falls over time, there is σ-convergence. When the partial correlation between growth in income over time and its initial level is negative, there is β-convergence. Two types of convergence are normally tested in empirical research.

• 1.    β convergence is tested as to determine whether or not poor countries are growing faster than richer countries (a negative correlation between initial per capita income and growth in per capita income ;

• 2.    σ convergence tests whether or not the dispersion between per capita income levels declines over time.

That first kind of convergence is liable to result in convergence of the second kind, but this process is offset by new disturbances that tend to increase dispersion

There are two types of β convergence across a number of developing countries, unconditional and conditional β convergence. Unconditional β convergence, which ignores all other possible impacts on growth, suggests that overtime countries with differing levels of initial GDP per capita will converge with one another over the long run. Whilst conditional β convergence involves all other possible impacts on growth.

Economists have recognized that β-convergence is not a sufficient condition for σ-convergence (for an early recognition of this idea see Barro and Sala-i-Martin 1992, pp. 227-28 , regardless of the literature’s stress on it. Also, Quah (1993 and

19

Friedman (1992) both approved of σ-convergence gets greater interest because it tells directly as to whether the distribution of income across economies is becoming more equitable.

This paper allows us to know that β-convergence is indeed a necessity σ-convergence’s condition but not quite sufficient for it. Then, we discuss the evidence of β-convergence in Indonesia using district-level data covering 1986–2010 and containing over 277 cross-sectional observations. We demonstrate that σ-convergence could not be detected during that time period in mentioned region or within the large majority of the individual provinces of Indonesia considered separately. But in many cases, that statistically significant σ-divergence is found.

METHODOLOGY AND DATA

• 1 .β Convergence

To derivation β convergence, Barro and Martin use the neoclassical growth model. The model neoclassical has a production function Y=F(K,L,T with assume

• 1.    Constant Return to Scale

F(λK,λL,Τ)=λF(K,L,Τ)=λΥ λ˃0

• 2.    Diminishing return

progress. In a closed economy, k^̂ changes as

k^̂̇ = f(k^̂ ) - ĉ - (δ+x+n) k^̂(2

where ĉ = C/ Le^xt, n is the growth rate of L, and δ is the rate of depreciation.

Household maximize utility

U = ∫₀^∞ u(c)e^nt e^-ρt dt(3

where c = C/L, ρ is the rate of time preference, and

c^1-θ -1(4

^u(c)1-θ

with θ ˃ 0, so that marginal utility, (u’(c)), has the constant elasticity ‒ θ with respect to c. (We assume ρ > n + (1-θ)x under to satisfy the transversality condition .

FOC for maximizing U in equation (3 requires

ĉ^c = θ¹ [f’ (k̂) - δ - ρ] (5

In the steady state, the effective quantities, ŷ, ĉ and k, do not change and the per capita quantities, y, c, and k, grow at the rate x. The level of k in the steady state satisfies

dF dF d²F d²F

dK > ^0, dL > ^0, dK² < ^0, dL² < ^0,

f’ (k^̂ *) = δ + ρ + θx

(6

• 3.    Inada Condition

lim ∕ ^dF ∖ _ lim ∕ ^dF ∖ _ ∞

K'⁰ (dK ) ■ '⁰ (dL ) ^θ°

lim ∕ ^dF ∖ _ lim ∕ ^dF ∖ _ 0

(K→∞) (dK )   (L→∞) (dL )

• 4.    Essentiality

F(0,L) = F(K,0) = 0. No input no production.

If the production function divided by Le^xt, then per unit income is

ŷ = f( k̂ )                                   (1

where k^̂ and ŷ are capital and output per unit of effective labor, L is labor (or population , and x is the rate of exogenous, labor-augmenting technological

if the production function is Cobb-Douglas, soŷ = f(k =Ak^α, where 0 ˂ α ˂ 1. Hence if two economies have the same parameters of technology and preferences, then the key result is that the initially poorer economy-with a lower starting value of k-tends to grow faster in per capita terms.

The transitional dynamics can be quantified by using a log linearization of equations (2 and (5 about the steady state. The solution for log[ŷ(t)] in the log-linearized estimate to the model with a Cobb-Douglas technology is

log[ŷ(t)] = log[ŷ(0)] e^-βt + log(ŷ*)(1 - e^-βt) (7

where the positive parameter β, which manages the speed of adjustment to the steady state, is given by the formula

2β={ψ²+4(-⅛αχρ+δ+θx)[e+t+θx-(n+δ+x)]}τ -ψ, (8)

where ψ = ρ - n - (1-θ)x>0

The average growth rate of y over the interval between dates 0 and T is

H^ ]=χ + 1?4⅛]  (9)

The higher β, the greater the responsiveness of the average growth rate to the gap betweenlog (ŷ*) and log [ŷ(0)], that is, the more rapid the convergence to the steady state. The model implies conditional convergence in that, for given x and ŷ*, the growth rate is higher the lower ŷ(0).

Equation (9 can be rewrite as

_y(T)'          1_-e^β          1_-e^β

• 1    ¹°g[⅛τ ] = ^{x +    1}°g (y*)^-v ¹<y≡

T y(0) T            T

(10

• 2 . σ Convergence

More recently, Furceri (2005 presents a related demonstration based on an OLS estimator of the coefficient on initial income.

(11

where 0 < β <1 and u_ithas mean zero, finite variance, σU, and is independent over t and i. Because a is assumed constant across economies, balanced growth paths are identical. Rewrite equation (11 yields,

(12 ∖Λi,t-l/

hence, β>0 indicates a negative correlation between growth and initial log income.

The sample variance of log income in t is given by

(13

where μ_t is the sample mean of log income. The sample variance is close by to thepopulation variance when N is large, and equation (11 can be used to

develop the evolution of σ², so we get

Gt = (l-tf⅛ι + ⅛

(14

the difference equation is stable only if 0<β<1, therefore β-convergence is necessary for σ-convergence. Given 0<β<1, the steady-state variance is

(σ²)

[i-(i-/?)²]

(15

hence, the cross-sectional dispersion falls with β but rises with σU. To combine equations (14) and (15) yields

(16

The solution, which is a first-order linear difference equation with constant coefficients, is given by

(17

where c is an arbitrary constant. Therefore, as long as 0˂ β ˂1, we have |1 ‒ β| ˂1, which implies that

Iim (1 - β)^2t = 0

t→∞

Thus,

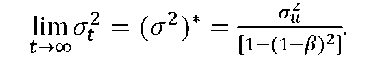
Furthermore, such as (1 ‒ β)>0, the approach to (σ² * is monotonic.

The change of variance, its increase or decrease toward steady-state’s value, is depending on the initial σ0. Automatically, economies can be β-converging toward one another while, at the same time, random shocks are pushing them apart. Despite that β-convergence, we would see if by chance the initial dispersion of income levels is small relative to the variance of random shocks then the dispersion of incomes will converge toward steady-state’s value from below.

β-convergence does not imply that σ-convergence arise when the parameter a varies across economies. Consider there are two economies, A and B, where both economies begin at the same level of income. However, assume that A begins on its balanced growth path while B, in the other hand, begins far below its balanced growth path, and assume that

β-convergence holds. The initial variance (σ²) will be zero, but σ_t² will grow over time as B grows faster than A and approaches a higher balanced growth path. Because indeed, β- convergence is the reason for the increasing variance.

• 3.I ndonesian District-level data

The paper brings us to make of the district-level data of Indonesia to study income growth from 1986 to 2010. The said data set consists of 277 district-level observations due correspond with amount counties in 1986 that have complete data.

The real per capita income measure that fits the definition is used by the Central Bureau of Statistics in Indonesia (BPS . Due to our lack of useful measures of price levels or price indexes for individual districts, we deflate the nominal values for each district by the province index for consumer prices. Since we use the same price deflator for each district in a single year, the particular deflator that we use affects only the constant terms in the subsequent regressions. The use of same deflator for each district leads to two types of potential measurement error. For the first type, if relative purchasing power parity does not hold over the district, then the growth rates of real per capita income are mismeasured. In other cases, the second type is it, if absolute purchasing power parity does not hold, hereafter the levels of real per capita income are mismeasured. It is adjusted to be demonstrated in per capita 2002 using the Indonesian province GDP deflator. Real per capita income levels are expressed as natural logs and values are considered for both 1986 and 2010.

Evidence on β Convergence for Indonesia

We use the data on real per capita income, y, for a cross section of the Indonesia district, i = 1, ..., N. Equation (10 imply that the average growth rate over the interval between any two points in time, to and to + T, is given by

(18

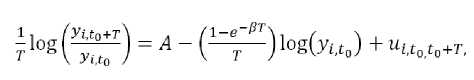
where A=

which is independent of i because we assumed ŷ_i^* = ŷ^*and x_i = x, the term u_i,t0,t0+T is a distributed lag of the error terms,u_it, between dates t₀ and t₀ + T. The coefficient A shifts because of the trend in technology with a change in the starting date, t₀.The term y is per-capita GRDP in district i at period T;

i,t₀+T

y_i,t is the initial per-capita GRDP in district i; A is the

intercept of the equation; and u_{i,t 0 ,t0 +T,} is average of the errors terms between periods 0 and T. If there is a negative association between theinitial per capita GRDP and the growth rate per capita GRDP, the β convergence exists.

The coefficient on log(y_it0)in equation (17) is-(1-e^-βT /T, which declines in magnitude with the length of the interval, T, for a given β. WhenT gets larger, the effect of the initial position on the average growth rate gets smaller; whenT tends to infinity, the coefficient tends to zero. We estimate β nonlinearly to take account of the associated value of T in the form of equation (17 . Then, we should obtain similar estimates of β regardless of the length of the interval.

To simplify equation (18 rewrite to

(19

where Growth_i: Average economic growth in the district i, using the formula

1 βinc_itn+τ∖

Growth_i = — In I----^:----I

• ^τ ∖ ^incU₀ ∕

with period 1986-2010, T=24, so the formula is

1    βinc_i 2oιo ∖

Growth_i = — In I -—^:---I.

24 ∖mc_il986J

ln inc_i(t₀ : logarithm natural real per capita income for the region i at the beginning of period.

This paper uses dummy variable for regions of Indonesia that are western, middle and eastern. It aims to find out there are differences between regions in Indonesia in terms of the rate of labor-augmenting technological progress and value’s steady state. To do this, we must select a base group; we choose western. The model becomes:

Growth_i=α₀ + α₁ ln inc_i (t₀) + α₂midle + α₃eastern + v_i    (20

The results of estimation indicate that absolute beta convergence exists. It means poor districts or regions shows the tendency to grow faster than rich ones. The results can be seen in the table 1 that show coefisien of initial per capita income with negative value. Equation with regional dummies has a bigger value of speed of convergence than basic equation except line 3 (1992-1997 .

Table 1. Regression for Personal Income Across Indonesia Districts

Basic Equation			Equation With Regional Dummies
Period      α̂ 1	-A β̂	R2[σ̂]	α̂ 1	β̂	R2[σ̂]
-0.0070 1986 - 2010 (0.00224)	0.77%	0.0346 [0.0201]	-0.0083 (0.0022)	0.92%	0.0964 [0.0196]
-0.0109 1986 ‒ 1991 (0.0041)	1.12%	0.0249 [0.0369]	-0.0125 (0.0041)	1.29%	0.0628 [0.0363]
-0.0099 1992 ‒ 1997 (0.0073)	1.02%	0.0067 [0.0659]	-0.0076 (0.0074)	0.78%	0.0216 [0.0656]
-0.0145 1998 ‒ 2003 (0.0056)	1.51%	0.0235 [0.0583]	-0.0176 (0.0056)	1.84%	0.0657 [0.0573]
-0.0047 2004 ‒ 2010 (0.0032)	0.48%	0.0080 [0.0339]	-0.0069 (0.0031)	0.7%	0.0719 [0.0329]

Notes: Standard errors of coefficients are shown in parentheses. The All equations have 277 observations. The estimation uses OLS, where speed of convergence, β̂ , calculated from α₁= that we get in OLS. Line 1 shows estimate of the overall sample for all period (1986-2010 . Line 2-4 show estimate of overall sample for each 5 years.

Does σ Convergence exist in Indonesia?

Considering the evidence, it is quite clear that it verifies the existence of β-convergence, which is a necessary condition for σ-convergence as we learned before. Here, using the same district-level data, we explore whether or not σ-convergence is occurring in Indonesia.

The paper will also examine σ convergence by computing the dispersion of district per-capita GRDP of Indonesia regions. Barro and Sala-i-Martin (2004, p. 462 say that the dispersion can be measured by calculating the standard deviation of per-capita logarithm for each year. The following formula will be used to estimate the standard deviation for each year:

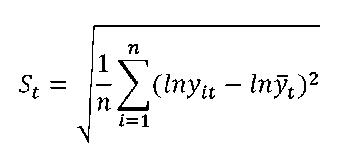
(21

where, S_t stands for standard deviation at period t, ln y̅_t and ln y_it represent the logarithm of the average per capita PDRB of Indonesian district at period t and the logarithm of per capita GRDP in district i at period t respectively, whereas n is the number of regions. If S_t+1is less than St the σ convergence exists.

However, if S_t+1 is more than S_t the σ convergence doesn’t exist.

The calculation of standard deviation of per-capita logarithm for both Indonesia and the provinces in Indonesia is shown in Table 2 that reports crosssectional for the entire sample of Indonesia district and for each of the 25 province, and the associated p-values for a variance ratio test of the null that the ratio of the two standard deviations is unity (against the one-tailed alternative . The 2010 standard deviation for the full Indonesia, sample (0.5401 is about 12 % greater than that of 1986 (0.6583 , a difference that is significant at the 1% level. In only 2 out of 25 provinces (Sumatera Barat and Kalimantan Tengah is the 2010 standard deviation significantly less than that of 1986 (at the 10% level or better . On the other hand, for 7 provinces the 2010 standard deviation is significantly larger than that of 1986 (at the 10% level or better . Hence, for many individual provinces, as well as for the full Indonesia, σ-divergence occurred from 1986 to 2010.

Table 2. Standard Deviations of Indonesia District’s Log Per Capita Income, 1986 vs 2010

		1986 per capita income	2010 per capita income
Region	Number of Districts	Standard deviation	Standard deviation	p-value
Indonesia	277	0.5401	0.6583	0.000527
Aceh	10	0.7389	0.3783	0.329382
Sumut	17	0.3289	0.3680	0.017169
Sumbar	14	0.4190	0.2263	0.049365
Riau	7	0.2477	0.5143	0.011025
Jambi	6	0.3104	0.4081	0.281477
Sumsel	10	0.6185	0.4586	0.192988
Bengkulu	4	0.5934	0.3460	0.199685
Lampung	4	0.4853	0.2486	0.150544
DKI	5	0.2827	0.5544	0.110197
Jabar	24	0.4227	0.5265	0.149693
Jateng	35	0.4496	0.5502	0.121975
Yogyakarta	5	0.3144	0.4455	0.258058
Jatim	37	0.5127	0.6817	0.045878
Kalbar	7	0.4271	0.2630	0.131549
Kalteng	6	0.2306	0.1127	0.071157
Kalsel	10	0.1491	0.4258	0.002254
Sulut	5	0.3875	0.5203	0.290962
Sulteng	4	0.1271	0.0924	0.30684
Sulsel	23	0.2198	0.3194	0.043391
Sultra	4	0.1525	0.3908	0.078279
Bali	8	0.1507	0.2909	0.051956
NTB	6	0.2301	0.2171	0.450655
NTT	12	0.2100	0.1842	0.335705
Maluku	5	0.3422	0.4435	0.313724
Papua	9	0.8623	0.8775	0.480829

Notes: Per capita income figures are in natural log form. p-values are based on a variance ratio test where the null hypothesis is that the value of the ratio of the 1986–2010 standard deviations is unity (against the two-tailed alternative .

Figure 1. Distribution of Indonesia Districts’ Log Per Capita Income, 1986 vs 2010

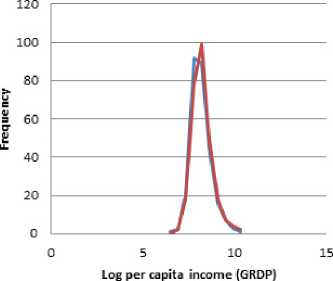
Frequency 1986

Frequency 2010

Quah (1997, 27 and Desdoigts (1999,306 have suggested that interpreting measures of dispersion may be straightforward if the distributions are

unimodal. As Figure 1 demonstrates, the distribution of income is unimodal for both 1986 and 2010 for Indonesian district-level data. Also figure 1 visually confirms that σ-convergence is not present.

Conclusions

Based on our verifiable results of this essay concerning the existence of convergence in the sense, that when economies are further below the steady-state position they tend to grow faster in per capital terms. This occurrence exposes clearly for Indonesian district over various periods from 1986 to 2010. Over long samples, poor states tend to grow faster in per capita terms than rich states even if we do not hold constant any variables other than initial per capita income.

In this paper, we show that β-convergence is indeed a necessity σ-convergence’s condition but not quite sufficient for it. We discuss evidence of β-convergence in the Indonesia using district-level data for the 1986 to 2010 period. And therefore, using the same data, we show that σ-convergence was not present during that time period in Indonesia or within a large majority of the provinces in Indonesia considered separately. In many cases, in fact, statistically significant σ-divergence is found.

What way should we take to reveal the presence of β-convergence and evidence of σ-divergence? If Indonesia was approaching its steady-state income variance from below during the 1986-2010, then two interpretations suggest themselves. First, the initial distribution of income was narrow in 1986 relative to the distribution of balanced growth paths. Second, the 1986 (2010) draw of county-specific shocks had a small (large sample variance relative to the population variance of shocks.

Another interpretation is that the variance of the balanced growth paths themselves increased. However, one may consider this second interpretation unlikely considering the relative institutional homogeneity of counties across the Indonesia and especially within individual province where the same β-convergence and σ-convergence results hold in many cases.

REFERENCES

Barro, Robert J., and Xavier X. Sala-i- Martin. (1992      “Convergence.”Journal of

Political Economy, 100, pp. 223–51.

Quah, Danny T. (1997 “Empirics for Growth and Distribution: Stratification, Polarization, and Convergence Clubs.” Journal of Economic Growth, 2, pp. 27–59.

Young, Andrew T., Higgins, Matthew J. and Levy Daniel (2008 , “Sigma Convergence versus Beta Convergence: Evidence from U.S.

County-Level data”, Journal of Money, Credit and Banking, Vol. 40, N0 5, pp. 1083 – 1093

Barro, Robert J., and Xavier X. Sala-i-Martin.

(2004 Economic Growth. Cambridge, MA: MIT Press.

Desdoigts, Alain. (1999 “Patterns of Economic Development.”Journal of Economic Growth, 4, pp. 305–30.

Friedman, Milton. (1992 “Do Old Fallacies Ever Die?” Journal of Economics Literature, 30, pp. 2129–32.

Furceri, David. (2005 “β and σ-Convergence: A Mathematical Relation of

Causality.” Economics Letters, 89, pp. 212–5.

Quah, Danny T. (1993 “Galton’s Fallacy and the Convergence Hypothesis.” Scandinavian. Journal of Economics, 95, pp. 427 -43.

25