Model Regresi Logistik pada Kelulusan Ujian Sertifikasi Pengadaan Barang dan Jasa Pemerintah
on
JEKT ♦ 9 [1] : 80 - 84
ISSN : 2301 - 8968
Model Regresi Logistik pada Kelulusan Ujian Sertifikasi Pengadaan Barang dan Jasa Pemerintah
Rukini*)
Badan Pusat Statistik Kabupaten Grobogan
ABSTRAK
Model regresi merupakan alat untuk menganalisis hubungan antara variabel respon dan variabel prediktor. Model regresi logistik digunakan saat variabel responnya bersifat kualitatif. Model yang sesuai diperoleh setelah dilakukan penaksiran parameter, uji signifikansi dan uji kecocockan model. Tujuan dari penelitian ini adalah untuk mengetahui pengaruh usia, masa kerja dan jenis kelamin peserta ujian sertifikasi pengadaan barang dan jasa pemerintah terhadap kelulusan. Studi kasus ujian sertifikasi pengadaan barang dan jasa pemerintah di Pusdiklat BPS RI gelombang II Tahun 2015. Data yang digunakan sebanyak 194 orang.Hasil pengolahan data menunjukkan bahwa usiamempunyai pengaruh yang signifikan terhadap tingkat kelulusan ujian sertifikasi pengadaan barang dan jasa pemerintah. Semakin banyak peserta ujian sertifikasi pengadaan barang dan jasa pemerintah usia kurang dari 35 tahun, maka kecenderungan untuk lulus semakin meningkat.
Kata kunci: sertifikat keahlian pengadaan barang dan jasa, organisasi pengadaan barang jasa, regresi logistik
Logistic Regression Models on Certification Test of Procurement of Government Goods and Services
ABSTRACT
The regression model a means to analyze the relationship between response variable and the predictor variables. Logistic regression model is used when response variable is qualitative. The appropriate model obtained after parameter estimation, significance test and compatibility test models. The goal of this research was to determine the effect of age, years of service and gender of participants exams towards graduation. The case study certification exams government procurement of goods and services to wave II Pusdiklat BPS RI Year 2015. The data used as many as 194 people. The processing results show that age has a significant influence on level the graduation certification exams of government procurement of goods and services. The more participants certification exam government procurement of goods and services for less than 35 years of age, the increasing tendency to pass .
Keywords: certificates of expertise procurement, procurement organization, logistic regression
PENDAHULUAN
Pemerintah dalam menjalankan fungsi pemerin tahannya, sudah pasti dibutuhkan logistik, peralatan dan jasa guna menunjang optimalnya kerja instansi tersebut.Kebutuhan ini dipenuhi oleh beberapa pi hak, baik itu perusahaan milik pemerintah maupun swasta.Berbeda dengan pengadaan barang dan jasa di instansi dan perusahaan swasta, pengadaan barang dan jasa di instansi pemerintahan lebih rumit karena berhubungan dengan perhitungan APBN/APBD yang digunakan untuk membayar barang atau jasa terse but. Terlebih lagi ada beberapa aturan yang menga tur proses pengadaan barang dan jasa tersebut, tata
cara pengadaan barang dan jasa diatur dalam Perpres 54 tahun 2010 yang kemudian diperbaharui dengan Perpres 70 Tahun 2012 dan perubahan yang terakhir atau perubahan keempat dari Perpres No. 54 Tahun 2010 yaitu Perpres 4 tahun 2015. Berdasarkan Per pres tersebut organisasi pengadaan barang dan jasa (Pejabat Pembuat Komitmen (PPK), Unit Layanan Pengadaan (ULP)/Pejabat Pengadaan) harus me miliki sertifikat pengadaan barang dan jasa, artinya pengadaan barang dan jasa itu tidak bisa dilakukan oleh sembarang orang. Pengertian sertifikat keahl ian pengadaan barang dan jasa adalah tanda bukti pengakuan dari pemerintah atas kompetensi dan ke mampuan profesi di bidang Pengadaan Barang Jasa.
Seiring dengan penerapan aturan yang baru di
harapkan semua instansi dapat melakukan proses pengadaan barang dan jasa dengan baikdan diharap kan dapat mengatasi kendala dan permasalahan yang dihadapi dalam pengadaan barang dan jasa. Selain mensyaratkan PPK,ULP/Pejabat Pengadaan memiliki sertifikat juga mensyaratkan memiliki disiplin yang tinggi bertanggung jawab, memiliki kemampuan managerial, memahami pekerjaan serta memaha mi proses pengadaan yang dilaksanakan. Sehingga masing masing Kementerian/ Lembaga/ Departe men/ Instansi (K/L/D/I) mempersiapkan SDM yang mampu dan mau untuk mengikuti ujian sertifikasi pengadaan barang dan jasa pemerintah. Tak jarang peserta melakukan sekali ujian sertifikasi pengadaan barang dan jasa langsung lulus. Berdasarkan hasil ujian sertifikasi peserta BPS yang dilaksanakan di Pusdiklat BPS RI pada Gelombang II tahun 2015, ternyata tidak mudah untuk mencapai kelulusan 100 persen. Sekitar 50 persen yang dinyatakan lulus, padahal dalam ujian tersebut diperbolehkan mem buka Perpres. Hal inilah yang menjadi penting untuk diteliti lebih lanjut faktor apakah yang mempengaruhi kelulusan ujian sertifikasi pengadaan barang dan jasa pemerintah tersebut. Pengetahuan hubungan kelulu san dengan faktor yang mempengaruhinya menjadi hal penting untuk mempermudah proses pengadaan barang dan jasa pemerintah. Jika hubungan itu dapat diketahui maka langkah langkah yang diambil dapat lebih terarah. Model statistik yang dipakai secara luas untuk mengetahui hubungan antara variabel respon dan variabel prediktor adalah analisis regresi. Model regresi yang diterapkan pada saat variabel respon nya bersifat kualitatif adalah model regresi logistik.
Uji kecocokan model harus dilakukan pada model regresi logistik. Kurang cocoknya model dapat memberikan kesimpulan yang salah terhadap data hasil observasi. Uji kecocokan diperlukan untuk mengetahui apakah model statistik sudak layak atau belum yaitu menggunakan uji Hosmer dan Lemeshow.
Model regresi logistik
Model regresi merupakan alat untuk menganalisis hubungan antara variabel respon dan variabel prediktor. Regresi logistik merupakan model regresi yang digunakan bila variabel responnya bersifat kualitatif, (Hosmer dan Lemeshow, 1989).Menurut Kuncoro (2001, hal:217) regresi logistik cukup baik dan sering digunakan karena regresi logistik memiliki beberapa keuntungan dibanding regresi lainnya. Regresi logistik tidak memerlukan asumsi normalitas, heteroskedastisitas, dan autokorelasi dikarenakan variabel terikat yang terdapat pada regresi logistik
merupakan variabel dummy (0 dan 1), sehingga residualnya tidak memerlukan ketiga pengujian tersebut. Model regresi logistik sederhana yaitu model regresi logistik untuk satu variabel prediktor X dengan variabel respon Y yang bersifat dikotomi. Nilai variabel Y = 1 menyatakan adanya suatu karakteristik dan Y = 0 menyatakan tidak adanya suatu karakteristik. Menurut Hosmer dan Lemeshow (1989) model regresi logistik yang dipengaruhi oleh p variabel prediktor dapat dinyatakan sebagai nilai harapan dari Y dengan diberikan nilai X .
⎛p⎞ ∣βo + ∑βkXk I l k=1 /
dengan 0 ≤ E(Y | x) ≤ 1 dan Y mempunyai nilai o atau 1. Nilai E(Y | x) merupakan probabilitas sukses, sehingga dapat dinyatakan dengan p(x), sehingga persamaan (1) menjadi
p βo +∑ βkXk
⎛p ⎞
∣βo+∑β^k I .......................................(2)
P (x) = —
1 + el k=' '
dengan βk menyatakan parameter-parameter regresi, xk adalah pengamatan variabel prediktor ke k dari sejumlah p variabel prediktor. Transformasi logit diterapkan pada model regresi logistic seperti pada persamaan (3) berikut.
Logit (p (x)) = g (x) = In
P (x )
1- P(x)
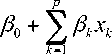
....................(3)
Transformasi logit bertujuan untuk membuat fungsi linear dari parameter parameternya. Fungsi g (x) linear terhadap parameter dan memiliki range (-∞, ∞), tergantung dari range variabel prediktor X.
Penaksiran Parameter Model
Metode penaksiran parameter yang banyak digunakan dalam regresi logistik adalah metode maksimum likelihood. Setiap observasi untuk model regresi logistik adalah variabel random dari distribusi Bernoulli, (Netter et al., 1996). Menurut Hosmer dan Lemeshow (1989), fungsi likelihood distribusi Bernoulli untuk n sampel independen adalah seperti dirumuskan pada Persamaan (4).
n
I (β) = ∏ p (x)Yi(i - p (x))1-Yi
2
βk ⎤
/V Λ I
SE βk ) .............................................
dan log-likelihood atau logaritma natural fungsi probabilitas bersamanya dirumuskan pada persamaan (5) berikut.
n
L β) = In ∏ p(X,) Y (1- p CX, ))1-Y
n
Y β + βι Xi)
∑ In [1 + expβ0 + β χ )]
Taksiran parameter βk, diperoleh dengan mendiferensialkan fungsi log-likelihood terhadap β k ,dengan k = 0,1. Nilai maksimum diperoleh bila hasil diferensial fungsi log-likelihood bernilai nol.
Uji Signifikansi Parameter
Pengujian ini dilakukan untuk mengetahui apakah taksiran parameter yang diperoleh berpengaruh secara signifikan terhadap model atau tidak, dan seberapa besar pengaruh masing masing parameter tersebut terhadap model.Uji signifikansi terdiri dari dua tahap yaitu uji signifikansi parameter model secara bersama dan uji signifikansi parameter model secara terpisah.
Uji signifikansi parameter model secara bersama dilakukan dengan uji rasio likelihood. Menurut Hosmer dan Lemeshow (1989), suatu statistik uji rasio likelihood G adalah fungsi dari L0 dan L1 yang berdistribusi (Chi-square) dengan derajat bebas p (banyaknya variabel prediktor yang ada dalam model) yang didefinisikan sebagai Persamaan (6) berikut.
G = -2(Lo - Li) ................................................(6)
dengan L 0 adalah log - likelihood dari model tanpa variabel prediktor, sedangkan L1 adalah loglikelihood dari model dengan p variabel prediktor. Nilai log-likelihood dihitung berdasarkan persamaan (5). Hipotesis nolnya adalah βk = 0, untuk semua k = 1, 2, ..., p, yang berarti bahwa semua variabel prediktor tidak signifikan terhadap model. Hipotesis nol ditolak jika G > X(2a.p) ataunilai signifikansi < 0,05 dapat dikatakan variabel signifikan di dalam model.
Uji Wald Chi-square digunakan untuk menguji signifikansi parameter model secara terpisah. Uji Wald Chi-square didefinisikan dengan persamaan (7) berikut.
dengan k=1,2,…,p
Statistik uji Wk mendekati distribusi Chi-square dengan derajat bebas 1. Hipotesis nolnya adalah βk = 0, untuk setiap k = 1, 2, ..., p, yang berarti bahwa variabel prediktor ke k tidak signifikan terhadap model. Hipotesis nol ditolak jika Wk > X(2a .1) atau nilai signifikansi <0,05.
Uji Kecocokan Model
Uji kecocokan model digunakan untuk mengevaluasi cocok tidaknya model dengan data, nilai observasi yang diperoleh sama atau mendekati dengan yang diharapkan dalam model. Cocok tidaknya model regresi logistik dinilai dengan menggunakan uji Hosmer dan Lemeshow. Jika uji Hosmer dan Lemeshow dipenuhi maka model mampu memprediksi nilai observasinya atau dapat dikatakan model dapat diterima karena sesuai dengan data observasinya.
Uji Hosmer dan Lemeshow yang ditulis dengan uji C , dihitung berdasarkan taksiran probabilitas, (Hosmer dan Lemeshow, 1989).Statistik uji Hosmer dan Lemeshow C yang dihitung berdasarkan nilai y = 1 dirumuskan pada Persamaan (8).
C = ∑ (or - n p,r
-
⅛ nr Pl r (l - Pl r )’
dengan plr menyatakan rata-rata taksiran probabilitas sukses kelompok ke r, or adalah jumlah sampel kejadian sukses dalam kelompok ke r, nr g
adalah total sampel kelompok ke- r, dan ∑ nr = n, dengan r = 1, 2, …, g. Statistik uji C mendekati distribusi Chi-Square dengan derajat bebas g-2, (Hosmer dan Lemeshow, 1989). Hipotesis nol menyatakan bahwa model cocok dengan data. Hipotesis nol ditolak jika C2 > X2 „atau nilai signigikansi <0,05.
-
a . g 2)
DATA DAN METODOLOGI
Data yang digunakan dalam penelitian ini adalah data peserta ujian sertifikasi pengadaan barang dan jasa pemerintah yang dilaksanakan oleh BPS gelombang II tahun 2015 bertempat di Pusat Pendidikan dan Pelatihan (Pusdiklat) BPS RI. Jumlah peserta sebanyak 194 peserta dari pegawai BPS di beberapa BPS Provinsi/ Kabupaten/ Kota se Indonesia. Adapun variabel respon adalah hasil ujian sertifikasi pengadaan barang dan jasa pemerintah. Sementara variabel prediktor meliputi usia peserta,
Tabel 1. Variabel Penelitian
|
Variabel |
Kode |
Kategori |
|
Hasil Ujian (Y) |
0 |
Tidak lulus |
|
1 |
Lulus | |
|
Usia (X1) |
0 |
>35 Tahun |
|
1 |
<35 Tahun | |
|
Masa Kerja (X2) |
0 |
>10 Tahun |
|
1 |
<10 Tahun | |
|
1 |
Laki laki | |
|
Jenis Kelamin (X3) |
2 |
Perempuan |
|
Sumber: desain penelitian, 2016 Tabel 2. Overal Test |
|
Omnibus Test of Model Coefficients | ||||
|
Chi-square |
df |
Sig. | ||
|
Step 1 |
Step |
45,898 |
3 |
,000 |
|
Block |
45,898 |
,000 | ||
|
Mode |
45,898 |
3 |
,000 | |
Sumber: hasil olah data, 2016
Hasil Uji Signifikansi Secara Keseluruhan Overall Test)
Formula hipotesis pada pengujian keseluruhan ini, dijabarkan sebagai berikut: (i) Ho : βjk =0, untuk semua j=0,2 dan k=1,2,… (maka tidak ada variabel predictor yang berpengaruh); (ii) H1: Terdapat paling tidak satu variabel predictor yang berpengaruh. Penentuan hasil statistik uji adalah Tolak H0 jika nilai signifikansi < 0,05. Berikut Tabel 2 menjabarkan hasil olah data overall test.
Hasil pengujian secara keseluruhan dapat disimpulkan bahwa nilai Chi-Square sebesar 45.832 dengan signifikansi 0,000 yang berarti bahwa dengan tingkat keyakinan 95 persen, ada minimal satu variabel bebas yang berpengaruh pada variabel tak bebas (variabel prediktor). Sehingga dapat disimpulkan bahwa model dapat digunakan untuk analisis lebih lanjut.
Tabel 3. Partial Test
|
Variables in the Equation | |||||||
|
B |
S.E |
Wald |
df |
Sig. |
Efp(B) | ||
|
Step 1a |
Usia(1) |
2,615 |
,748 |
12,216 |
1 |
,000 |
13,666 |
|
Masa_kerja(1) |
,180 |
,708 |
,064 |
1 |
,800 |
1,197 | |
|
JK(1) |
,233 |
,339 |
,472 |
1 |
,492 |
,792 | |
|
Constant |
1,908 |
,781 |
5,967 |
1 |
,015 |
,148 | |
Sumber: hasil olah data, 2016
Keterangan : a. Variable(s) entered on step 1: Usia, Masa_kerja, JK
masa kerja dan jenis kelamin. Penelitian ini menggunakan analisis regresi logistik, karena variabel responnya bersifat kualitatif sehingga dibentuk variabel dummy (0 dan 1). Adapun langkah langkah dalam pembentukan model regresi logistik meliputi penaksiran parameter, signifikansi parameter dan uji kecocokan model.
HASIL DAN PEMBAHASAN
Analisis data yang digunakan dalam penelitian ini adalah analisis statistik yang dilakukan dengan menggunakan bantuan software SPSS versi 16. Langkah pertama yang dilakukan yaitu uji penaksiran parameter metode yang banyak digunakan adalah metode maksimum likelihood dengan alasan lebih praktis (Nachrowi dan Usman, 2002). Metode maksimum likelihoood ini menduga parameter dengan nilai yang memaksimumkan fungsi likelihood (likelihood function).
Langkah kedua yaitu uji signifikansi parameter yang terdiri dua tahap yaitu uji signifikasi parameter model secara keseluruhan (overall test) dan uji signifikasi secara parsial (partial test). Masing masing hasil tahapan pengujian selanjutnya akan dijabarkan pada pembahasan berikut.
Hasil Uji Signifikansi Secara Parsial Partial Test)
Formula hipotesis pada pengujian parsial ini adalah sebagai berikut: (i) Ho : βjk = 0, (variabel prediktor ke-k pada g j (x) tidak signifikan terhadap model); dan (ii). Ho : βjk ≠ 0, (Variabel prediktor ke k pada g j (x) signifikan terhadap model). Penentuan hasil statistik uji adalah Tolak H0 jika nilai signifikansi < 0,05. Tabel 3 menjabarkan hasil perhitungan statistic terhadap olah data pada uji signifikansi parsial.
Hasil uji secara parsial dapat ditunjukkan bahwa dengan tingkat keyakinan 95 persen variabel usia signifikan mempengaruhi kelulusan. Hal ini ditunjukkan dengan nilai signifikansi sebesar 0,000 dan kurang dari 0,05. Sementara variabel masa kerja dan jenis kelamin tidak signifikan mempengaruhikelulusan.
Langkah ketiga uji kelayakan ataupun kesesuaian model, apakah model itu layak secara statistik. Hal tersebut diantaranya telah dilakukan diawal yaitu overall test dan partial test. Kriteria statistik lainnya adalah uji kelayakan model dan classification plot. Hasil uji statistic dari kedua kriteria uji ini akan dibahas satu persatu pada pembahasan berikut.
Tabel 4. Hasil Uji Kelayakan Model
Hosmer and Lemeshow Test
Step Chi-square df Sig.
1 1,969 4 ,742
Sumber: hasil olah data, 2016
Tabel 5. Ketepatan Model
Classification Table
|
Observed |
Predicted | ||
|
Hasil ujian |
Percentage Correct | ||
|
Tidak Lulus |
Lulus | ||
|
Step 1 Hasil Ujian Tidak lulus |
48 |
50 |
49,0 |
|
Lulus |
7 |
89 |
92,7 |
|
Overall Percentage |
70,6 | ||
Sumber: hasil olah data, 2016
Keterangan : a. Cut value adalah 0,500
Uji Kelayakan Model
Formula hipotesis pada uji kelayakan model penelitian ini adalah: (i) H0 : Model telah cukup mampu menjelaskan data/ sesuai; dan (ii) H1 : Model tidak cukup mampu menjelaskan data. Kriteria hasil pengujian adalah Tolak H0 jika nilai sig < 0,05. Hasil olah data statistic uji kelayakan model dijabarkan pada Tabel 4.
Berdasarkan hasil output pada Tabel 4 terlihat bahwa nilai signifikan sebesar 0,740 yang berarti lebih besar 0,05. Sehingga dapat disimpulkan dengan tingkat keyakinan 95 persen dapat diyakini bahwa model regresi logistik yang digunakan telah cukup mampu menjelaskan data/sesuai.
Clasification Plot
Kriteria statistik berikutnya adalah classification plot. Hasil olah data ketepatan model dengan menggunakan kriteria klasifikasi ini, diuraikan pada Tabel 5. Hasil pada Tabel 5 menunjukkan bahwa model regresi logistik yang dihasilkan telah cukup baik, karena mampu menebak dengan benar 70,6 persen kondisi yang terjadi.
SIMPULAN
Berdasarkan hasil pembahasan dapat dirumuskan beberapa simpulan penelitian sebagai berikut: (i) model regresi logistik yang diperoleh adalah p
g(x) = β> + ∑ βkχk dimana g(χ) = -1,908 + 2,615χ1 + 0,180x2 – 0,233x3; (ii). Variabel yang berpengaruh terhadap kelulusan hasil ujian sertifikasi pengadaan barang dan jasa pemerintah adalah variabel usia. Semakin banyak peserta ujian usia kurang dari 35
tahun kemungkinan lulus semakin meningkat; (iii). Jika dilihat secarastatistik bahwa variabel masa kerja (X2) dan Jenis Kelamin (X3) tidak signifikan, bukan berarti pengaruhnya tidak ada, melainkan ada pengaruhnya hanya saja pengaruhnya sangat kecil.
SARAN
Saran yang dapat disampaikan berdasarkan hasil penelitian ini adalah, pada penelitian lanjutan perlu menambahkan variabel prediktor lainnya seperti informasi pengalaman pernah berapa kali mengikuti ujian serupa sebelumnya serta tingkat pendidikan. Harapannya adalah agar hasil dari model yang didapatkan lebih akurat.
REFERENSI
Hosmer, D.W, and Lemeshow, S. (1989). Applied Logistic Regression. John Willey, New York.
Mudrajad Kuncoro(2001).Metode Kuantitatif (Teori dan Aplikasi untuk Bisnis dan Ekonomi), Unit Penerbit dan Percetakan AMP YKPN, Yogyakarta.
Nachrowi Djalal dan Hardius Usman (2002). Penggunaan Tehnik Ekonometri. Jakarta:PT Raja Grafindo Persada.
Netter, J., Kutner, M.H., Nachtseim, C.J and Wasserman, W.
(1996). Applied Linier Statistical Models. Fourth edition. The McGraw Hill Companies, Inc., United States of America.
Peraturan Presiden Republik IndonesiaNo. 54 Tahun 2010Tentang Pengadaan Barang/Jasa Pemerintah.
Peraturan Presiden Republik Indonesia No. 70 Tahun 2012 Perubahan kedua atas Peraturan Presiden No. 54 Tahun 2010 Tentang Pengadaan Barang/Jasa Pemerintah.
Peraturan Presiden R epublik Indonesia No 4 Tahun 2015Perubahan keempat atas Peraturan Presiden No. 54 Tahun 2010 Tentang Pengadaan Barang/Jasa Pemerintah.
Pusat Pendidikan dan Pelatihan (Pusdiklat) BPS RI, Data Peserta Ujian Sertifikasi Pengadaan Barang dan Jasa Pemerintah Gelombang II Tahun 2015.
84
Discussion and feedback