Carrier Frequency Offset Effects on OFDM System over Rayleigh Fading Channel

Journal of Electrical, Electronics and Informatics, Vol. 3 No. 2, August 2019

45

Carrier Frequency Offset Effects on OFDM System over Rayleigh Fading Channel

N.M.A.E.D. Wirastuti¹, I.G.A.K. Diafari D. Hartawan², I.M.A. Suyadnya³ and D.C. Khrisne⁴

¹Department of Electrical Engineering, Faculty of Engineering, Udayana University, Badung, Indonesia

Email: dewi.wirsatuti@unud.ac.id

• ^2,3,4Department of Electrical Engineering, Faculty of Engineering, Udayana University, Badung, Indonesia

Abstract Orthogonal Frequency Division Multiplexing (OFDM) system showed the use of Discrete Fourier Transform (DFT) and Inverse Discrete Fourier Transform (IDFT) to perform the baseband modulation and demodulation. So that, it can increase and improve the efficiency of the modulation and demodulation. Currently, the OFDM is being utilized in the field of broadband wireless communication, which transmit signals orthogonally, that increases speed of information transmission. It also has high proficiency with high bandwidth and provide large data rates and robust against the multipath delay spread. On the other hand, there are some issues faced OFDM system which are high Peak Average Power Ratio (PAPR), and sensitive to Phase Noise (PN) and Carrier Frequency Offset (CFO). This paper presents Orthogonal Frequency Division Multiplexing (OFDM) performance evaluation in the presence of CFO with two different environment scenarios were used: an AWGN channel and a Rayleigh fading channel. The simulation was performed to evaluate the effects of CFO based on Bit Error Rate (BER) vs. Energy Bit per Noise Ratio (Eb/No). The results showed that for BER degradation caused by CFO effects have presented in our simulation for both AWGN and Rayleigh fading channel.

Index Terms—Fading channel, Carrier Frequency Offset, Bit Error Rate, Energy Bit per Noise Power Ratio

• I.    Introduction¹

Due to the high flexibility that Orthogonal Frequency Division (OFDM) offers including bandwidth (BW) efficiency and its high tolerance for induced distortion [1], the OFDM has been considered as the modulation techniques in several applications from cellular systems (3GLTE, WiMAX, Long Term Evolution (LTE), wireless local area networks (LANs), digital audio radio, underwater communications, optical light modulation, Digital Audio Broadcasting (DAB); Digital Video Broadcasting (DVB); Mobile Broad Band Wireless Access (MBWA) [2,3,4].

The performance of OFDM suffers from a frequency offset caused by Doppler shift due to the relative motion between transmitter and receiver, and the differences between the frequencies of the local oscillators at transmitter and receiver [4]. Indeed, the carrier frequency offset gives rise to ICI, thereby destroying the orthogonality of the OFDM data [5]. So that it is importance

to estimate and compensate for the CFO. Several schemes have been proposed to estimate the CFO of OFDM signals such as CFO estimation scheme using a training symbol with two identical halves [6], utilizes a training symbol with more than two identical parts [7], using the maximum-likelihood (ML) criterion [8], and using an envelope equalization process and periodogram operations [9].

The carrier frequency offset effects in OFDM have been investigated in [1,2] with an AWGN channel. Furthermore, [3,4] examine the presence of carrier frequency offset in multi-path fading channels. Several methods have been developed to reduce the effect of frequency offset [6-9]. In this paper, carrier frequency offset estimation will not be discussed.

The rest of the paper is organized as follows. Section 2 describes system model of the simulation process. Then, the simulation parameters and results are presented in Section 3. Finally, and conclusions are presented in section 4.

• II. Method and Procedures

• III. Results and Analysis

• A.    System Model with AWGN Channel

The OFDM system model for an AWGN channel with carrier frequency offset can be described briefly as in Figure 1. The disturbance by frequency offset is modelled as a multiplicative distortion introduced in the channel.

e 2πnε/N    n(n)

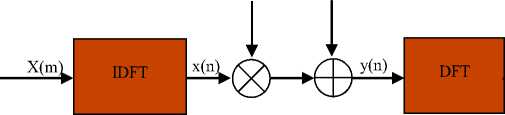
Fig. 1. OFDM with frequency offset model.

Assuming perfect frequency and timing synchronization and carrier frequency offset that does not change during one OFDM symbol, the received OFDM signal y(n) can, in the presence of frequency offset, can be expressed as

• A. Simulation Parameter

Numerical values for the OFDM parameters used in the simulation are detailed in Table 1.

Table 1 OFDM parameters used in the simulation

	Parameter	Value
	FFT size	64
Y(k)	Modulation	QPSK
——>	Eb/No Number of pilot sub-carriers (Nsp) Number of data sub-carriers (Nsd) Total number of sub-carriers (Nst) Useful symbol part (Nu) Number of cyclic prefix (Ncp) Total sub-carriers on each OFDM symbol (NT) Useful symbol part duration (Tu) Cyclic prefix duration (Tcp) OFDM symbol duration (Ts)	Range: 0 to 10 dB 4 48 52 64 16 80 3.2 μs 0.8 μs 4 μs

j 2πnε

y(n) = x(n)e N +n(n) 1),

(1)

where x(n) is the time-domain transmitted symbol, ε is the normalized frequency offset given by ΔfNt_s with Δf is the frequency difference between transmitter and receiver carrier frequencies, t_s is the sub-carrier symbol period. n(n) is the AWGN channel and N is the total number of subcarriers. The effect of carrier frequency offset after passing y(n) through the DFT block can be analyzed as

N_-1        — j 2 ^mk

Y ( k ) = ∑ y ( ^m )e ⁿ ’

m=0

(2)

• B.    System Model with Fading Channel

Figure 2 shows a simple OFDM model with multi-path fading and an AWGN channel with carrier frequency offset. Using the same assumption as mentioned above, the received OFDM signal y(n) in the presence of frequency offset with fading channels can be expressed as

L -1

y (n) = ∑ h(Y)x(n - Y)e    ⁿ + n (n).    (3)

Y=0

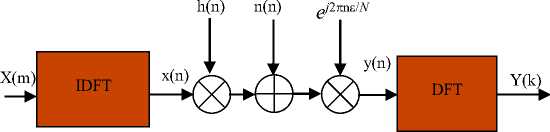
Fig. 2. OFDM and frequency offset model in fading channel.

• B.    Simulation Results

Figures 3 and 4 depict the effect of carrier frequency offset on the BER performance at the receiver of OFDM in AWGN and Rayleigh fading channels, respectively. QPSK is employed without channel coding, interleaving and clipping effect. Perfect symbol timing is assumed. Other parameters used in this simulation have been mentioned in Sub-section III.A. Here ε is the normalized carrier frequency offset, which is a fraction of the sub-carrier spacing.

For example, for an AWGN channel, at Eb/No=8, for a negligible BER degradation of about 0.5, the maximum tolerable frequency offset cannot exceed 1% of the subcarrier spacing. In a Rayleigh fading channel, the maximum tolerable frequency offset cannot exceed 4% of the subcarrier spacing for a negligible BER degradation of about 0.3.

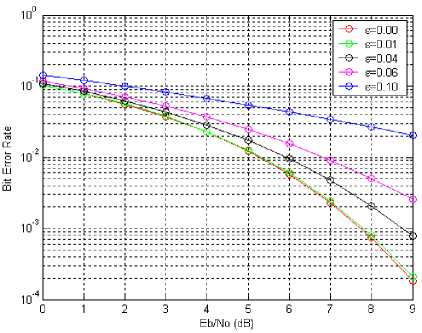
Fig. 3. BER vs. Eb/No performance for OFDM with ε=0.01, 0.04, 0.06 and 0. 1 over an AWGN channel, no cancellation scheme is applied.

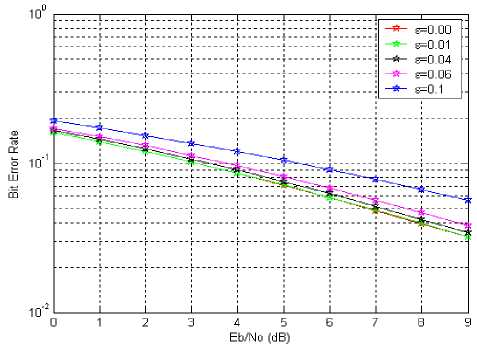
Fig. 4. BER vs. Eb/No for OFDM with ε=0.01, 0.04, 0.06 and 0. 1 in Rayleigh fading channels, no cancellation scheme is applied.

• [5]    K. Sathananthan and C. Tellambura, “Probability of error calculation ofOFDM systems with frequency offset,”IEEE Trans. Commun., vol. 49, no. 11, pp. 1884–1888, Nov. 2001.

• [6]    T.M. Schmidl, D.C. CoxRobust frequency and timing synchronization for OFDM, IEEE Trans. Commun, 45 (12) (1997), pp. 1613-1621.

• [7]    S. Chang, E.J. “Powers Efficient frequency-offset estimation in OFDM-based WLAN  systems”,  Electron. Lett, 39 (21) (2003),

pp. 1554-1555.

• [8]    M.-H. Cheng, C.-C. Chou, “Maximum-likelihood estimation of frequency and time offsets in OFDM systems with multiple sets of identical data”, IEEE Trans. Sig. Process, 54 (7) (2006), pp. 28482852.

• [9]    G. Ren, et al., “An efficient frequency offset estimation method with a large range for wireless OFDM systems”, IEEE Trans. Veh. Technol, 56 (4) (2007), pp. 1892-1895

• IV. Conclusion

The performance of OFDM in the presence of phase noise and carrier frequency offset effects has been evaluated through simulation. Two different environment scenarios were used: an AWGN channel and a Rayleigh fading channel. Our analysis has shown that intercarrier interference are introduced by carrier frequency offset for both scenarios. The main conclusion that we can draw from the simulated BER vs. Eb/No. For BER degradation caused by carrier frequency offset effects have presented in our simulation show that for a negligible BER degradation of about 0.5 the maximum tolerable frequency offset is less than 1% of the sub-carrier spacing in AWGN channel. In a Rayleigh fading channel, for a negligible BER degradation of about 0.3, the maximum tolerable frequency offset is less than 4% of the sub-carrier spacing.

Acknowledgment

Authors thank Institute for Research and Community Service, Udayana University for financial support through Penelitian Unggulan Udayana funding.

References

• [1]    Z. Wang and G. B. Giannakis, “Wireless multicarrier communications:Where Fourier meets Shannon,”IEEE Signal Process. Mag., vol. 17 no. 3, pp. 29–48, May 2000.

• [2]    Jungwon Lee ; Hui-Ling Lou ; D. Toumpakaris ; J.M. Cioffi., “Effect of carrier frequency offset on OFDM systems for multipath fading channels”, IEEE Global Telecommunications Conference, Dallas, TX, USA, 2004.

• [3]    Shagun Sharma, Khushal Thakur., “Carrier frequency offset in OFDM systems”. 2^nd International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 19-20 Jan. 2018.

• [4]    3GPP TR 25.814 V7.1.0, 3rd Generation Partnership Project;

Technical Specification Group Radio Access Network; Physical layer aspects for evolved Universal Terrestrial Radio Access September 2006.