Calibration of the BMP280 and ESP-12S Based Wireless Atmospheric Pressure Measure Equipment Using a Pressure Chamber
on
Buletin Fisika Vol 23 No. 1 February 2022 : 1 – 11
Kalibrasi Alat Pengukur Tekanan Atmosfer Nirkabel Berbasis BMP280 dan ESP-12S Menggunakan Pressure Chamber
Calibration of the BMP280 and ESP-12S Based Wireless Atmospheric Pressure Measure Equipment Using a Pressure Chamber
Arief Laksono*, I Gusti Agung Widagda
Program Studi Fisika, Fakultas MIPA, Universitas Udayana, Kampus Bukit Jimbaran, Badung, Bali, Indonesia 80361
Email: arief_laksono@student.unud.ac.id*, igawidagda@unud.ac.id
Abstrak – Dalam rangka mempelajari dan mempraktikkan metode kalibrasi alat ukur tekanan atmosfer meteorologi, telah dilakukan perancangan, perangkaian dan pengalibrasian alat ukur tekanan atmosfer nirkabel eksperimental berbasis sensor tekanan digital BMP280 dan System on Chip ESP-12S. Menggunakan standar tekanan sekunder barometer digital Vaisalla PTB330, alat dikalibrasi di dalam pressure chamber pada rentang tekanan 850-1050 hPa dengan batas toleransi maksimum ±0,15 hPa pada tingkat kepercayaan 95%. Berdasarkan hasil uji dari parameter koreksi dan U95, menunjukkan bahwa keandalan sistem antarmuka sensor dan metode aplikasi koreksi internal yang digunakan dalam proses kalibrasi memberikan hasil kalibrasi yang memenuhi syarat standar WMO. Uji kepresisian pada repeatability conditions berdasarkan ISO5725:1994 juga digunakan sebagai ukuran kepresisian alat. Melalui laporan kalibrasi ini, performa dan keakuratan sensor BMP280 dalam kaitannya dengan pengukuran pada objek meteorologi khususnya tekanan atmosferis dapat diketahui dan dipelajari lebih lanjut.
Kata kunci: Kalibrasi, pengaturan koreksi, alat ukur tekanan, tekanan atmosferis, keakuratan, kepresisian, BMP280, ISO5725:1994
Abstract – In order to study and practice the method of meteorological atmospheric pressure gauge calibration, the design, assembly and calibration of an experimental wireless atmospheric pressure gauge based on the BMP280 digital pressure sensor and the System on Chip ESP-12S has been carried out. Using the Vaisalla PTB330 digital barometer secondary pressure standard, the instrument is calibrated in the pressure chamber in the pressure range 850-1050 hPa with a maximum tolerance limit of ± 0.15 hPa at a 95% confidence level. Based on the test results of the correction parameters and U95, it shows that the reliability of the sensor interface system and the internal correction application method used in the calibration process provide calibration results that meet the requirements of the WMO standard. The precision test on repeatability conditions based on ISO5725: 1994 is also used as a measure of tool precision. Through this calibration report, the performance and accuracy of the BMP280 sensor in relation to measurements on meteorological objects, especially atmospheric pressure can be known and studied further.
Keywords: Calibration, correction adjustment, measuring device, atmospheric pressure, accuracy, precision, BMP280, ISO5725:1994
Tekanan atmosfer (tekanan) adalah kuantitas yang lazim digunakan untuk menggambarkan cuaca dan iklim pada suatu wilayah. Melalui pengukuran tekanan secara periodik tidak hanya dapat diperoleh informasi cuaca pada waktu tertentu, prakiraan objektif juga dapat dilakukan untuk mengetahui kecenderungan cuaca pada waktu mendatang. Informasi mengenai meteorologi selalu memiliki andil dalam kehidupan sehari-hari terlepas dari kesadaran umat manusia untuk memahami dan mengambil keputusan terhadap informasi tersebut. Agar usaha ini menghasilkan sesuatu yang berarti untuk publik, diperlukan keakuratan data meteorologi dan teknik pengolahan yang sesuai. Sensor tekanan digital
merupakan modernisasi dari alat ukur tekanan konvensional – barometer, dengan ukuran fisik yang lebih kecil, tanpa komponen mekanis, dan dapat dintegrasikan dengan berbagai sistem elektronik modern, miniaturisasi sistem sensor juga berujung pada konsumsi daya minimum. Pengintegrasian sensor tekanan digital Bosch Sensortec BMP280 dengan System on Chip ESP-12S merupakan upaya agar data pengukuran tekanan ini dapat diakses dengan mudah melalui jejaring publik pada suatu sistem infrastruktur digital berbasis Internet of Things, efektif memangkas pihak ketiga.
Keakuratan suatu alat ukur ditentukan dengan proses kalibrasi. Dalam kegiatan ini, kalibrasi terkait pada kesatuan antara sensor dan antarmuka yang membentuk alat ukur tekanan eksperimental yang telah dirancang dan dirangkai. Menggunakan standar sekunder barometer digital Vaisalla PTB 330 yang memenuhi standar meteorologi, kalibrasi dilakukan di dalam kamar yang dapat mengondisikan atmosfer di sekitar alat ukur. Kamar tersebut lazim disebut pressure chamber.
Selain digunakan untuk mempelajari metode kalibrasi meteorologis, alat ukur tekanan eksperimental juga dibuat untuk menguji metode penerapan koreksi yang umumnya didapat dari dalam laporan hasil kalibrasi. Kalibrasi dan penerapan koreksi yang baik menyebabkan hasil pengukuran dapat sesuai dengan Standar Internasional (SI), dengan jaminan bahwa untuk setiap hasil pengukuran yang didapat tidak akan lebih besar dari pada batas toleransi yang disetujui secara internasional (keakuratan). Pada batasan yang mungkin, melalui pengolahan hasil kalibrasi dapat ditentukan bilamana alat ukur tekanan eksperimental telah sesuai dengan standar alat ukur kemeteorologian (WMO).
Tekanan atmosferik atau juga disebut tekanan barometrik adalah berat yang ditimbulkan oleh atmosfer di
atas suatu luasan permukaan pada permukaan tersebut. Berdasarkan data pengamatan pada atmosfer,
tekanan berkurang secara eksponensial terhadap ketinggian. Pada ketinggian 80 km, tekanan hanya
bernilai 0,01 hPa. Jika dibandingkan dengan tekanan pada permukaan laut P(0), ini berarti 99,999% fraksi massa atmosfer berada di bawah ketinggian 80 km. Tekanan pada ketinggian tertentu P(z),
dirumuskan dalam persamaan barometrik [1]:
P (z) = P (0) exp
Magl- z 1
RT J
(1)
dengan Ma adalah massa molekul udara, g0 percepatan gravitasi, R konstanta gas ideal dan T adalah temperatur atmosfir.
Pada pressure chamber, pengkondisian tekanan dilakukan dengan memompa medium kalibrasi homogen masuk atau keluar pressure chamber. Pada gas ideal, persamaan (1) yang diubah dalam bentuk kerapatan atmosfer ρa(z):
( M g„ 1
Pa (z) = Pa (0) exp I±^ z I (2)
v RT J
menunjukkan kesebandingan antara ρa(z) dan ρa(0). Hal ini menjamin bahwa dengan mengubah kerapatan atmosfer yang terkondisikan melalui penambahan massa medium kalibrasi, pressure chamber juga dapat menciptakan kondisi atmosfer sesuai dengan persamaan barometrik. Supaya metode ini tidak mengubah karakteristik volume yang terkontrol dari tekanan terkondisi, temperatur di dalam pressure chamber harus dijaga kestabilanya.
-
2.2 Interpretasi koefisien determinasi pada tingkat kepercayaan tertentu
Analisis regresi sering digunakan untuk menyediakan model matematis yang dapat digunakan untuk memprediksi keluaran suatu sistem. Namun dalam kasus pemrediksian hasil, adalah subjektif dan abstrak jika harus menginterpretasi nilai koefisien determinasi (R²) tanpa diketahui batas minimal agar garis regresi dapat memberikan cakupan yang baik pada interval prediksi (PI) yang diharapkan. Olkin dan Finn (1995) telah mengembangkan pendekatan untuk menghitung standard error dari R², ketidakpastian dari R² dapat digunakan untuk menentukan rentang kepercayaan dari R² dengan faktor cakupan tertentu sesuai dengan persamaan:
R2 ± t„ , e (3)
(1-α, n - k-1) R v 7
Rentang yang didapat dari persamaan (3) menentukan batas nilai R² pada rentang kepercayaan yang ditentukan. Parameter uji student-t adalah nilai dari tabel statistik-t yang nilainya ditentukan berdasarkan
tingkat signifikan (α), jumlah data (n) dan jumlah prediktor pada persamaan regresi (k). Sementara untuk SE nilainya diberikan oleh pendekatan Olkin dan Finn [2]:
SER 2 ≈
' 4R2 (1 - R2 )2 (n - k-1) (n2 -1)(3 + n)
1
22
(4)
Dengan menggunakan tingkat kepercayaan 95%, jika nilai R² dari model regresi yang digunakan berada pada rentang yang dibentuk persamaan (3) terhadap nilai R² yang sempurna (R² = 0,9999) maka model regresi dikatakan dapat memberikan peluang cakupan terhadap pengamatan data paling kecil sebesar 95%, sehingga penginterpretasian R² dapat menunjukkan kelayakan model regresi secara konkrit dan objektif.
-
2.3 Standard-error-dari-regresi
Evaluasi ketidakpastian dalam suatu pengukuran dapat menggunakan berbagai metode statistik yang sesuai [3] dan standard error dapat dimanfaatkan dalam evaluasi ini mengingat sifat standard error yang sesuai dengan metode pengukuran yang umumnya dilakukan dalam penelitian (pembacaan berulang pada suatu titik uji). Demikian pada analisis regresi, hasil simulasi menunjukkan bahwa tiap-tiap data teramati dengan rentang kepercayaan 95%, tidak selalu menghasilkan peluang cakupan 95% terhadap nilai rata-rata, hal ini bertolak belakang dengan kebenaran empiris yang ditemukan pada data yang tersebar normal [4].
Pada model regresi yang memiliki residual besar, data di luar cakupan regresi, namun dengan perbedaan yang tidak terlalu signifikan sehingga data bukan merupakan outliers, harus ditangani dengan metode lain. Standard-error dari regresi yang juga dikenal sebagai standard-error-of-estimate (SEE), merupakan ukuran yang menyatakan jarak rata-rata nilai yang teramati terhadap garis regresi. SEE dapat digunakan untuk menyatakan derajat ketidakpastian regresi dalam satuan variabel respons, menginterpretasi keakuratan model regresi secara langsung. Perhitungan SEE didahului oleh permodelan regresi, kemudian menggunakan persamaan regresi terhadap nilai teramati untuk menghitung residu kuadrat dari nilai yang diprediksi dan yang teramati. Jika diintegrasikan dengan permodelan regresi linear dari sejumlah data n dalam hubungan antara data terikat y dengan data teramati x, SEE dinyatakan sebagai:
SEE =
1
n - 2
n
Σ( y.- y)
—
(5)
-
2.4 Repeatability conditions menurut ISO5725
Repeatability Conditions adalah kondisi dimana hasil-hasil pengukuran yang tidak bergantung satu sama lain didapat menggunakan metode yang sama, dari objek penelitian yang identik, pada laboratorium yang sama dan oleh operator yang sama menggunakan peralatan yang sama dalam rentang waktu yang singkat. Suatu objek penelitian pada repeatability conditions berpotensi menunjukkan kehisterisisan (penyebaran hasil suatu pengukuran dengan pengukuran yang lain), yang mana merupakan kriteria pengujian kepresisian suatu alat ukur. Pada suatu sistem alat ukur, kepresisian yang buruk akibat faktor histerisis menyebabkan meningkatnya ketidakpastian dari hasil pengukuran. Kepresisian pada repeatability conditions dinyatakan dalam standar deviasi repeatability (σr) merupakan akar kuadrat dari rata-rata varian dari tiap-tiap pengukuran berulang j dengan banyak datum n yang diperoleh dalam repeatability conditions:
σ2 r
Σ ,1 ( ni -1) σ
Σ i (n. -1)
(6)
Berdasarkan ISO5725 bagian 6, diperlukan minimal dua hasil pengukuran berulang untuk menentukan kepresisian pada repeatability conditions. Pada kasus “dua kelompok pengukuran pada satu laboratorium dalam repeatability conditions” akan ditemui rata-rata pengukuran berulang y dan y , σr dapat digunakan untuk menentukan batas maksimum dari Iy1 - y I agar hasil pengukuran yang dilakukan
dapat dikatakan presisi. Batas ini disebut critical difference (CD) yang pada peluang cakupan 95% nilainya mengikuti [5]:
CD = 1,96σ
,r
11
2 H--
2n 2n
2,8σ
,r
11
2n 2n
(7)
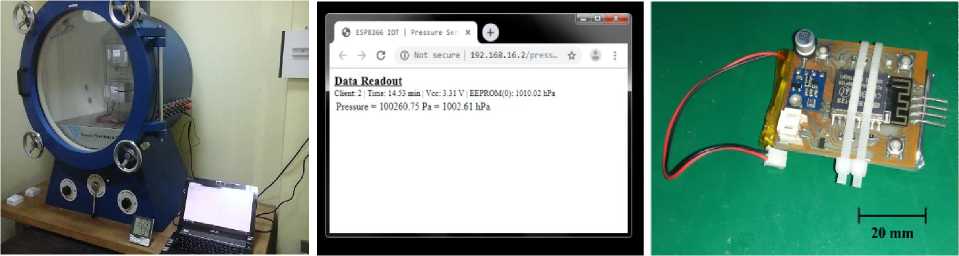
Objek utama kalibrasi pada kegiatan ini adalah alat ukur tekanan. Komponen utama dari alat ukur tersebut adalah ESP-12S yang menangani pembacaan sensor tekanan BMP280 dan antarmuka berbasis HTTP. Alat eksperimental ini dirancang sebagai alat ukur nirkabel yang bekerja dalam mode Software Access Point mampu terhubung dalam jangkauan 300 meter pandangan tanpa bantuan antena eksternal dan dapat diakses melalui SSID: “pressureSensorIOT”. Alat akan memberikan pembacaan tekanan secara realtime dengan interval sampling 5 detik, untuk memangkas waktu tunda transmisi (latency) selama proses kalibrasi (Gambar 1.a), alat ini diatur sebagai server lokal pada jaringan IP privat yang dapat diakses melalui laman “http://192.168.16.2/press” seperti yang ditunjukkan pada Gambar 1.b.
(a)
(b)
(c)
Gambar 1. (a) Proses pengalibrasian alat ukur, (b) antarmuka alat ukur dan (c) alat ukur eksperimental yang dibuat.
Secara umum, prinsip kerja dalam kegiatan ini adalah pengalibrasian dan pengaturan indikasi pengukuran alat secara berulang, dimulai dari kalibrasi awal dan pengaturan awal, pasangan kalibrasi – pengaturan akan diulang jika keluaran tidak sesuai standar. Alat ukur yang dibangun, memiliki keuntungan tersendiri dalam hal pengaturan keluaran, karena rancangan bersifat unik dan eksperimental, penulis memiliki akses terhadap rancangan internal serta arsitektur dan algoritma antarmuka, sehingga koreksi keluaran alat dapat diterapkan dengan relatif mudah.
-
3.1 Pengaturan awal dan metode penerapan koreksi
Sebelum proses kalibrasi, perlu dilakukan koreksi awal pada indikasi pengukuran oleh alat. Hal ini dilakukan untuk mengompensasi latency sistem BMP280-ESP-12S yang memediasi komunikasi antara sensor dan antarmuka terhadap hasil pembacaan pada waktu tertentu. Alur pengaturan disajikan pada Gambar 2.b, proses kalibrasi secara garis besar adalah membaca Pc pada standar sekunder dan indikasi keluaran alat, kemudian menyediakan hubungan berupa koreksi. Hasil dari sub-proses ini adalah “Hasil kalibrasi awal”.
Proses pada Gambar 2.a dirancang untuk mengubah koreksi internal alat ukur, proses ini mengandalkan dua parameter yang menentukan bilamana model curve fitting terpilih berpotensi mengoreksi indikasi pengukuran alat sehingga sesuai dengan standar pada tingkat kepercayaan tidak kurang dari 95%. Parameter tersebut adalah R² dan SEE yang dioperasikan antara indikasi pengukuran alat dengan nilai pengukuran standar sebagai variabel bebas. Menggunakan premis bahwa alat ukur akan memberikan respons yang linear pada perubahan standar uji yang linear, proses ini memiliki rencana cadangan bilamana ditemukan pada putaran pertama proses, model linear tidak memenuhi tingkat kepercayaan 95%. Spiess dan Neumeyer telah menyediakan analisa yang sah bahwa koefisien determinasi memiliki performa yang buruk untuk model non-linear, sebagaimana metode ini kehilangan presisi setelah 3 atau 4 angka di belakang koma [6]. Sementara, SEE dapat digunakan pada model linear dan non-linear [7], sehingga perhitungan SEE juga dilakukan untuk menyediakan informasi kelayakan model.
Pengaturan Internal Alat Ukur memerlukan masukan berupa hasil kalibrasi siap pakai yang harus disusun terlebih dahulu, pada kasus pengaturan awal, data ini didapatkan dari “Hasil kalibrasi awal”, metode ini juga dapat dipanggil pada proses lain yang memerlukan, asalkan ia diberi masukan berupa hasil kalibrasi siap pakai. Langkah terakhir proses ini berupa penerapan koreksi pada alat ukur, yaitu pengkodean persamaan model regresi ke dalam sistem alat ukur. Pada sejumlah n-iterasi (1,2,3,…,n) proses pengalibrasian-pengaturan, persamaan regresi dari indikasi alat pada iterasi ke-n yn(xn) diharapkan sama dengan nilai standar yang diberikan xn, maka regresi yn(xn) idealnya berupa fungsi dengan operan tunggal (unary function) tanpa koefisien regresi. Sebagai contoh untuk model linear, jika ditemukan regresi sesungguhnya yn(xn) bukan merupakan unary function (yrn=c0n + c1nxn), koreksi dilakukan sebagai berikut:
y - c y = y θ χ = 'n---n n rn n
c1n
Y _ yn c0n (8)
n c1n
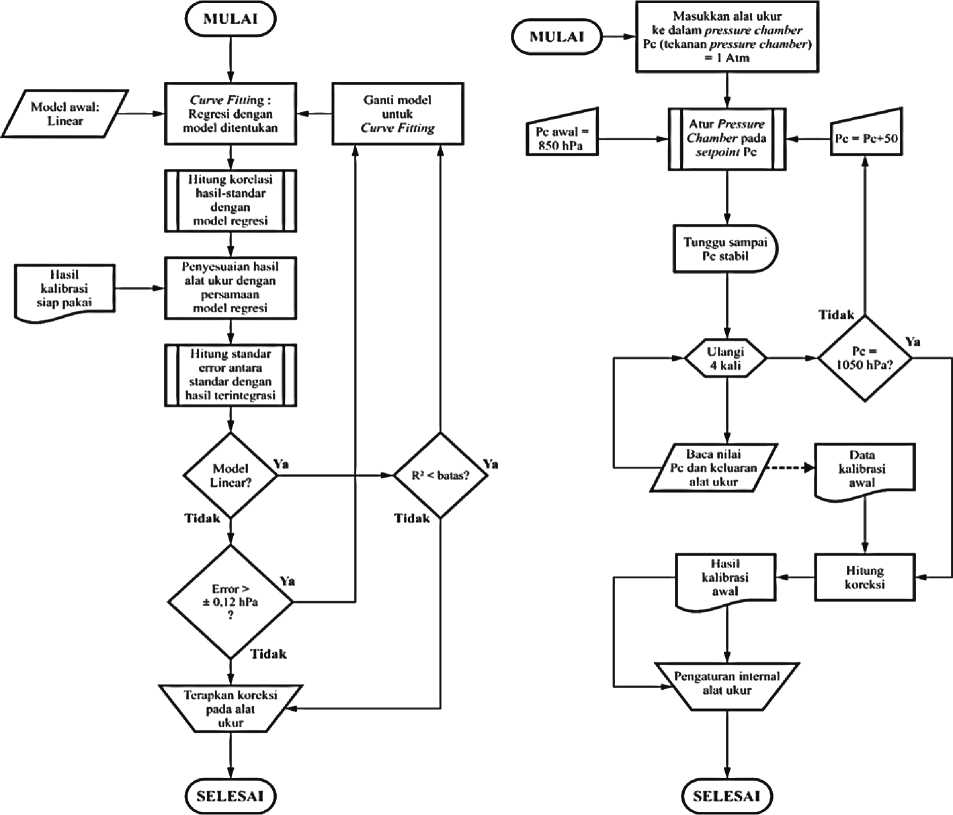
(a)
(b)
Gambar 2. (a) Diagram alir proses "Pengaturan Internal Alat Ukur” dan (b) Pengaturan awal alat ukur.
Metode serupa juga digunakan pada tahap “Penyesuaian hasil” pada Gambar 2.a untuk menghitung SEE. Pada pengintegrasian hasil, koreksi harus diterapkan pada setiap hasil keluaran yang terukur, hal ini berdampak langsung pada regresi Yn terhadap xn , yang akan menunjukkan model regresi sempurna (Yn /xn≈1), tetapi meskipun koreksi Yn diterapkan, hal ini belum tentu akan ditemui pada regresi yr(n+1)
terhadap x(n+1) karena faktor kesalahan acak ataupun kesalahan observasi yang mungkin terjadi pada iterasi selanjutnya, menghasilkan yrn(xn) yang unik untuk setiap n. Berdasarkan perhitungan dengan persamaan (3) dibuat keputusan bahwa pada peluang cakupan 95% terhadap korelasi sempurna batas minimum nilai R² = 99,9841% dan batas maksimum SEE = ±0,12 yang merupakan akurasi relatif dari BMP280. Batas-batas ini akan meminimalisir jumlah iterasi dan menghilangkan keraguan yang mungkin terjadi karena beberapa hasil yrn(xn) yang hampir identik.
-
3.2 Kalibrasi secara meteorologi alat ukur tekanan digital
Sejalan dengan apa yang diilustrasikan pada Gambar 3, proses kalibrasi alat ukur tekanan berakhir ketika alat ukur telah sesuai dengan standar, keputusan ini dilakukan dengan memperhatikan parameter koreksi dan ketidakpastian pada “Hasil kalibrasi siap pakai”. Data ini selain digunakan sebagai acuan dalam proses pengaturan internal alat ukur, juga dapat digunakan untuk menguji kepresisian alat ukur. Uji kepresisian CD-95% berdasarkan ISO5725 dan perhitungan SEE dilakukan untuk mengetahui tingkat keakuratan dan kepresisian alat ukur.
Sebelum ditentukan apakah alat sesuai dengan standar alat ukur kemeteorologian, keakuratan alat juga dibandingkan dengan data karakteristik alat ukur yang tersedia pada Datasheet Bosch Sensortec BMP280 Digital Pressure Sensor. Hal ini dilakukan untuk menyediakan rasa tentang seberapa masuk akal keluaran antarmuka sistem BMP280 dan ESP-12S terhadap performa pabrikan sensor.

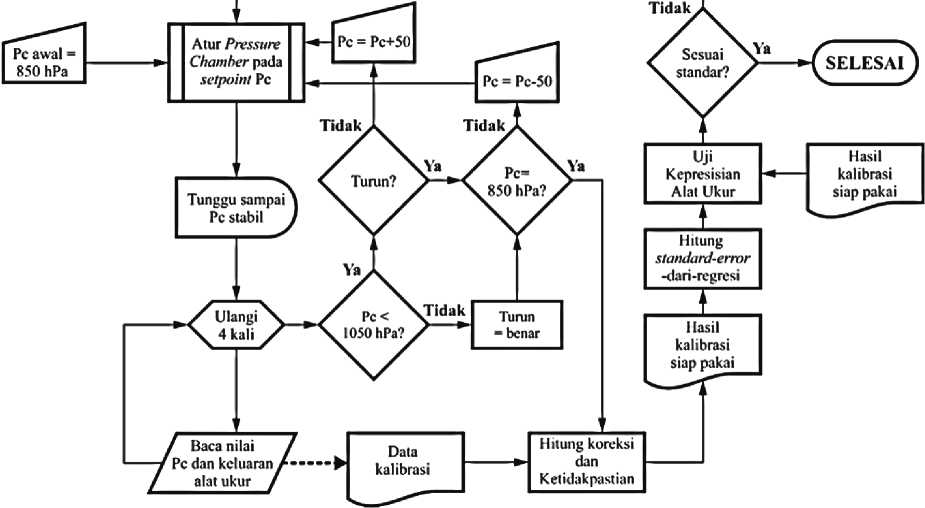
Gambar 3. Diagram alir proses kalibrasi alat ukur tekanan.
Pengoperasian pressure chamber serta pembacaan nilai standar sekunder dan indikasi alat dilaksanakan oleh operator yang sama dengan prosedur operasi standar yang berlaku. Rentang naik dan turun dari setpoint dirancang untuk menciptakan repeatability condition. Hal ini tidak dilakukan pada tahap pengaturan awal karena hasil kalibrasi awal tidak digunakan untuk menguji kepresisian alat ukur. Keseluruhan proses kalibrasi akan diulang sebanyak maksimum 5 kali, sebelumnya apabila kalibrasi gagal menemukan titik akhir, maka alat ukur tekanan dinilai gagal karena desain.
-
3.3 Performa sensor tekanan digital BMP280 terhadap standar WMO
Pada akhir proses kalibrasi diperoleh “data kalibrasi” yang selanjutnya digunakan untuk menyusun “laporan hasil kalibrasi”. Hasil kalibrasi merupakan tabel acuan yang digunakan pada pengukuran menggunakan alat yang bersangkutan. Penentuan status standarisasi alat pada metode di Gambar 3
menggunakan koreksi dan ketidakpastian yang diperluas U95. Pada pembacaan di sekitar titik uji, maka indikasi pengukuran alat terkalibrasi terhadap standar tekanan diberikan oleh:
Nilai Pengukuran = (Indikasi terbaca + koreksi) ± U95 hPa (9)
Nilai batas maksimum standarisasi U95 adalah sebesar ± 0,15 hPa. Nilai U95 tersebut tertelusur ke standar toleransi untuk alat ukur tekanan digital yang telah ditetapkan oleh World Meteorological Organization (WMO). Hasil kalibrasi dapat disusun dengan mempertimbangkan hasil uji kepresisian. Jika pengukuran di sekitar titik uji terbukti presisi pada repeatability condition, maka hasil yang dilaporkan adalah rata-rata dari kedua rentang titik uji [5].
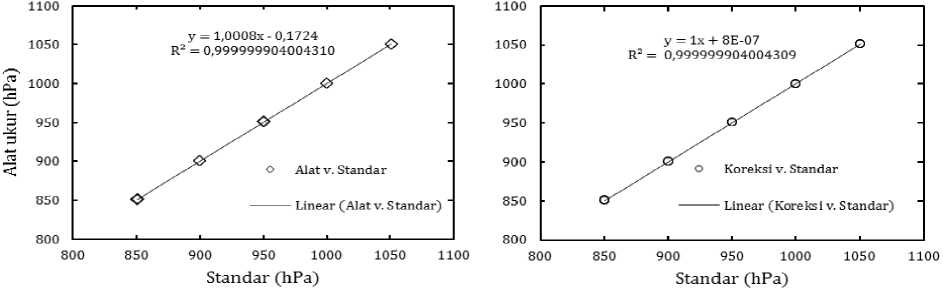
Dengan menggunakan Gambar 2.b pada proses manual Pengaturan Internal Alat Ukur, didapatkan hasil regresi antara indikasi pengukuran alat dan nilai standar seperti yang ditunjukkan oleh Gambar 4.a. Dapat teramati bahwa persamaan regresi bukan merupakan unary function, sehingga koreksi awal tetap harus dilakukan meskipun dalam metode pada Gambar 2.a dan 2.b tidak dilakukan pengambilan keputusan berdasarkan hasil ini. Uji linearitas antara indikasi pengukuran alat sebelum dan setelah dikoreksi menggunakan Persamaan (8) terhadap nilai standar yang digunakan pada proses kalibrasi awal ditunjukkan pada Gambar 4.
Hasil regresi pada Gambar 4.a memperlihatkan pesamaan linier y=1,0008x - 0,1724. Pada persamaan tampak terdapat gradien sebesar 1,0008 dan koefisien regresi sebesar -0,1724. Ini memberikan indikasi masih adanya potensi penyimpangan hasil pengukuran oleh alat ukur hasil rancangan terhadap hasil pengukuran standar. Dari hasil fitting diperoleh nilai koefisien determinasi R2 yang lebih tinggi dari pada nilai R2 minimum sebesar 99,9841% yang ditetapkan. Ini menunjukkan bahwa alat ukur yang dibuat memiliki kepresesian yang baik.
Jika dilakukan koreksi, diperoleh hasil pengukuran sebagaimana ditunjukkan pada Gambar 4.b. Diperoleh persamaan fitting
y = x + 8×10-⁷ (10)
Persamaan 10, tampak gradiennya sama dengan 1 (satu). Konstanta regresinya sama dengan 8×10-⁷, dapat diabaikan sehingga diperoleh persamaan regresi y=x. Dari Gambar 4.b, diperoleh nilai R2 yang lebih tinggi dari pada nilai R2 minimum yang ditetapkan. Ini memberikan petunjuk bahwa dengan menggunakan persamaan kalibrasi Persamaan (10) akan dapat diperoleh hasil pengukuran antara alat ukur standar dan hasil rancangan sangat mendekati sama (akurat) dan presesi.
(a)
(b)
Gambar 4. (a) Regresi Keluaran Alat terhadap Standar dan (b) Regresi Keluaran Alat Tersesuaikan terhadap Standar.
Menggunakan metode pada Gambar 3, alat ukur yang telah dikoreksi menurut persamaan regresi pada Gambar 4.a, dikalibrasi dan ditentukan status standarisasinya. Data hasil kalibrasi disajikan pada Tabel 1. Hasil kalibrasi khususnya “Koreksi” juga digunakan untuk menguji kepresisian alat ukur tekanan, sementara keakuratannya dapat diketahui melalui perhitungan SEE-95% dari “Keluaran Alat” terhadap “Tekanan Std”. Parameter koreksi digunakan dalam uji kepresisian mengingat pengaturan tekanan pada pressure chamber yang dilakukan secara manual. Hal ini mengakibatkan munculnya
ketidak-konsistenan dalam mencapai titik uji yang merupakan kandidat kuat penyebab rusaknya kepresisian alat. Karena koreksi pada dasarnya adalah selisih antara nilai tekanan dan indikasi alat ukur, ketidak-konsistenan ini dapat diatasi, dengan asumsi bahwa indikasi alat ukur tekanan memberikan respons yang sebanding.
Tabel 1. Data Kalibrasi Alat Ukur.
|
Titik Uji (hPa) |
Pembacaan |
Koreksi Std.a (hPa) |
Tekanan Std. (hPa) |
Keluaran Alat |
Koreksib (hPa) |
Std.Error Rata- |
|
Alat Standar (hPa) |
Hasil Rancangan (hPa) |
rata Keluaranc (hPa) | ||||
|
850₀ |
850,26 |
-0,07 |
850,19 |
850,12 |
0,07 | |
|
850,27 |
-0,07 |
850,20 |
850,13 |
0,07 | ||
|
850,28 |
-0,07 |
850,21 |
850,13 |
0,08 | ||
|
850,28 |
-0,07 |
850,21 |
850,12 |
0,09 | ||
|
850₁ |
850,37 |
-0,07 |
850,30 |
850,27 |
0,03 | |
|
850,38 |
-0,07 |
850,31 |
850,26 |
0,05 | ||
|
850,39 |
-0,07 |
850,32 |
850,29 |
0,03 | ||
|
850,40 |
-0,07 |
850,33 |
850,31 |
0,02 |
0,00573 | |
|
900₀ |
902,03 |
-0,06 |
901,97 |
901,99 |
-0,02 | |
|
902,04 |
-0,06 |
901,98 |
901,97 |
0,01 | ||
|
902,04 |
-0,06 |
901,98 |
902,03 |
-0,05 | ||
|
902,06 |
-0,06 |
902,00 |
902,08 |
-0,08 | ||
|
900₁ |
900,55 |
-0,06 |
900,49 |
900,53 |
-0,04 | |
|
900,55 |
-0,06 |
900,49 |
900,51 |
-0,02 | ||
|
900,55 |
-0,06 |
900,49 |
900,51 |
-0,02 | ||
|
900,56 |
-0,06 |
900,50 |
900,52 |
-0,02 |
0,01237 | |
|
950₀ |
950,75 |
-0,05 |
950,70 |
950,74 |
-0,04 | |
|
950,75 |
-0,05 |
950,70 |
950,78 |
-0,08 | ||
|
950,76 |
-0,05 |
950,71 |
950,77 |
-0,06 | ||
|
950,76 |
-0,05 |
950,71 |
950,79 |
-0,08 | ||
|
950₁ |
950,90 |
-0,05 |
950,85 |
950,92 |
-0,07 | |
|
950,90 |
-0,05 |
950,85 |
950,93 |
-0,08 | ||
|
950,91 |
-0,05 |
950,86 |
950,95 |
-0,09 | ||
|
950,92 |
-0,05 |
950,87 |
950,95 |
-0,08 |
0,00657 | |
|
1000₀ |
1000,61 |
-0,05 |
1000,56 |
1000,65 |
-0,09 | |
|
1000,60 |
-0,05 |
1000,55 |
1000,67 |
-0,12 | ||
|
1000,60 |
-0,05 |
1000,55 |
1000,64 |
-0,09 | ||
|
1000,61 |
-0,05 |
1000,56 |
1000,6 |
-0,04 | ||
|
1000₁ |
1000,11 |
-0,05 |
1000,06 |
1000,19 |
-0,13 | |
|
1000,11 |
-0,05 |
1000,06 |
1000,19 |
-0,13 | ||
|
1000,12 |
-0,05 |
1000,07 |
1000,2 |
-0,13 | ||
|
1000,13 |
-0,05 |
1000,08 |
1000,23 |
-0,15 |
0,00875 | |
|
1050₀ |
1050,56 |
-0,04 |
1050,52 |
1050,61 |
-0,09 | |
|
1050,56 |
-0,04 |
1050,52 |
1050,66 |
-0,14 | ||
|
1050,56 |
-0,04 |
1050,52 |
1050,62 |
-0,10 | ||
|
1050,58 |
-0,04 |
1050,54 |
1050,63 |
-0,09 | ||
|
1050₁ |
1050,58 |
-0,04 |
1050,54 |
1050,63 |
-0,09 | |
|
1050,58 |
-0,04 |
1050,54 |
1050,67 |
-0,13 | ||
|
1050,60 |
-0,04 |
1050,56 |
1050,62 |
-0,06 | ||
|
1050,60 |
-0,04 |
1050,56 |
1050,68 |
-0,12 |
0,00913 | |
|
Nilai |
SEE 95% = 0,06817 | |||||
-
a Koreksi standar didapatkan dari data kalibrasi barometer digital Vaisalla PTB330. b Koreksi = nilai standar – indikasi pengukuran alat. c Rata-rata (weighted average) dari masing-masing standard error pada rentang naik dan turun.
Perhitungan SEE terhadap “tekanan standar” dan “keluaran alat” menyediakan informasi tentang keakuratan alat ukur. Dari Tabel 1, hasil perhitungan SEE adalah sebesar 0,06817 hPa. Nilai SEE ini tidak lebih besar dari pada ±0,12 hPa yang mana merupakan keakuratan relatif dari sensor BMP280. Oleh karenanya hasil pengukuran alat hasil rancangan masih berada di dalam daerah spesifikasi sensor
BMP280. Hal ini memberikan indikasi bahwa alat ukur hasil rancangan memiliki tingkat keakuratan yang sangat baik.
Hasil kalibrasi khususnya “Koreksi” juga digunakan untuk menguji kepresisian alat ukur tekanan, hasil uji ini disajikan pada Tabel 2. Dari tabel tersebut dapat teramati bahwa tidak pada semua titik uji memperlihatkan nilai D≤CD-95%, artinya tidak semua rentang pengukuran memberikan hasil pengukuran yang presesi. Tidak konsistennya kepresisian menurut hasil perhitungan Cd-95% ini diduga akibat digunakannya parameter koreksi dalam uji kepresisian dimana pengaturan tekanan pada pressure chamber dilakukan secara manual. Tekanan yang rendah di dalam pressure chamber berpotensi menyebabkan timbulnya histerisis, dimana semakin rendah nilai tekanan, semakin tinggi kerentanan sistem pressure chamber terhadap gangguan, yang pada akhirnya dapat menimbulkan ketidakpresisian pada pengukuran sebagaimana tampak pada titik uji 850 hPa. Sementara karena tekanan pada 1000 hPa relatif lebih tahan terhadap gangguan dari lingkungan, dapat diduga bahwa ketidakpresisian disebabkan oleh faktor human error yaitu ketidakkonsistesian dalam mengatur tekanan pressure chamber. Akan tetapi nilainya relatif tidak jauh di atas CD-95% sehingga faktor kecacatan tersebut dapat dikesampingkan.
Tabel 2. Uji Kepresisian Alat Ukur
|
Titik Uji (hPa) |
koreksi (hPa) |
CD-95% [A] (hPa) |
Rata-rata Koreksi Naik [B] (hPa) |
Rata-Rata Koreksi Turun [C] (hPa) |
|B-C|=[D] (hPa) |
Presisi jika D ≤ A |
|
8500 // 850i |
0,0112 |
0,0157 |
0,0775 |
0,0325 |
0,045 |
SALAH |
|
9000 // 900i |
0,0283 |
0,0396 |
-0,0350 |
-0,0250 |
0,010 |
BENAR |
|
95Oo // 950i |
0,0147 |
0,0206 |
-0,0650 |
-0,0800 |
0,015 |
BENAR |
|
1OOOo // 1000ι |
0,0245 |
0,0343 |
-0,0850 |
-0,1350 |
0,050 |
SALAH |
|
1O5Oo // 1050i |
0,0280 |
0,0392 |
-0,1050 |
-0,1000 |
0,005 |
BENAR |
Ketidakpresisian pada kedua titik tersebut dapat ditangani melalui pengalibrasian ulang pada titik-titik tersebut. Tetapi dengan syarat analisis hasil harus dengan segera dilakukan dalam rentang waktu yang pendek sehingga hasil dari pengalibrasian ulang dapat memenuhi repeatability condition pada implementasi kalibrasi meteorologi [8].
Pada akhir proses kalibrasi diperoleh “data hasil kalibrasi. Data tabel hasil kalibrasi dapat disusun dengan mempertimbangkan Tabel 2 pada kolom uji kepresisian. Jika pengukuran di sekitar titik uji terbukti presisi pada repeatability condition, maka hasil yang dilaporkan adalah rata-rata dari kedua rentang titik uji [5]. Berdasarkan hasil kalibrasi nilai koreksi dan U95 sepanjang rentang titik uji seperti ditunjukkan pada Tabel 3. Dari tabel tersebut dapat teramati pada rentang pengukuran 850 - 1050 hPa nilai U95 tertinggi adalah 0,018 hPa. Nilai ini masih lebih rendah dari pada nilai U95 yang ditetapkan oleh WMO maksimum sebesar ±0,15 hPa. Sebagaimana diberikan oleh Persamaan (9), dengan nilai U95 yang lebih kecil tersebut memberi indikasi bahwa hasil pengukuran oleh alat ukur hasil rancangan akan berada di dalam rentang daerah hasil pengukuran oleh alat standar. Oleh karena itu hasil pengukuran alat ukur hasil rancangan adalah akurat.
Tabel 3. Hasil Uji Kalibrasi
|
Titik Uji (hPa) |
Rata-rata Tekanan Std. (hPa) |
Rata-rata Keluaran Alat (hPa) |
Koreksi (hPa) |
±U95 (hPa) |
|
850* |
850,26 |
850,20 |
0,05 |
0,011 |
|
900 |
901,24 |
901,27 |
-0,03 |
0,024 |
|
950 |
950,78 |
950,85 |
-0,07 |
0,013 |
|
1000* |
1000,31 |
1000,42 |
-0,11 |
0,017 |
|
1050 |
1050,54 |
1050,64 |
-0,10 |
0,018 |
Lebih lanjut uji linearitas, sebagaimana yang disajikan pada Gambar 5 memberikan hubungan antara nilai standar terhadap indikasi pengukuran oleh alat ukur tekanan hasil rancangan. Hubungan yang digunakan adalah nilai standar terhadap indikasi pengukuran alat ukur hasil rancangan, bukan sebaliknya seperti pada kondisi kalibrasi, karena ketika operasional alat diharapkan dapat memberikan pembacaan seperti tekanan standar.
Meskipun telah memenuhi standar, namun dari Gambar 5 tampak bahwa persamaan regresinya adalah
y=1,0008x - 0,7003 (11)
Tampak masih memiliki gradien dan konstanta regresi, serupa dengan persamaan linier pada Gambar 4 tetapi dengan konstanta regresi yang lebih besar. Nilai koefiesien R² masih lebih besar dari pada 99,9841%. Kedua hal ini menunjukkan bahwa hasil pengukuran alat ukur hasil rancangan menyimpang dari alat ukur standar (kurang akurat) tetapi memiliki tingkat kepresesian yang baik. Hal ini kemungkinan karena pada pengambilan keputusan standarisasi berdasarkan metode pada Gambar 3 digunakan kalibrasi menurut persamaan regresi pada Gambar 4.a.
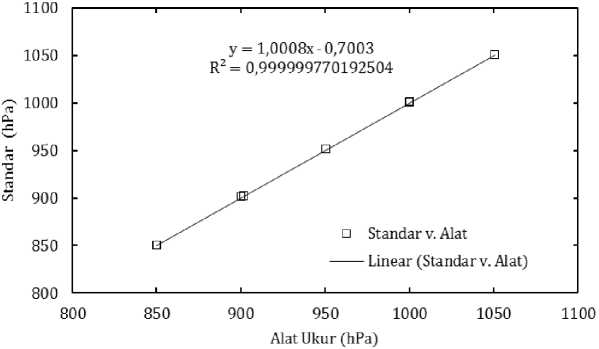
Gambar 5. Regresi Nilai Standar Terhadap Keluaran Alat Ukur.
Telah dilakukan kalibrasi pada alat ukur tekanan atmosfer nirkabel eksperimental berbasis BMP280 dan ESP-12S terhadap data sekunder standar tekanan Vaisalla PTB330 antara 800 – 1050 hPa. Hasil uji lineritas memperlihatkan nilai R2 yang lebih besar dari pada nilai R2 = 99,9841% yang ditetapkan, Ini menunjukkan bahwa pada tingkat kepercayaan 95% alat ukur hasil rancangan memiliki tingkat kepresisian yang sangat baik. Hasil uji U95 maksimum ±0,018 hPa, lebih kecil dari pada nilai U95 = ±0,15 yang diizinkan oleh WMO. Didukung oleh hasil perhitungan SEE=0,06817 hPa yang mana lebih kecil dari pada batas maksimum keakuratan sensor BMP280 yaitu ±0,12 hPa maka alat ukur hasil rancangan memiliki tingkat keakuratan yang baik. Oleh karenanya dapat disimpulkan bahwa alat ukur hasil rancangan layak untuk digunakan pada rentang pengukuran tekanan atmosfer antara 850 – 1050 hPa.
Ucapan Terima Kasih
Penulis menyampaikan terima kasih kepada Balai Besar Meteorologi Klimatologi dan Geofisika Wilayah III Denpasar Bali yang telah menyediakan sarana dan prasarana pengamatan dan pembelajaran proses pengalibrasian tekanan atmosferik.
Pustaka
-
[1] D. D. Jacob, Introduction to Atmospheric Chemistry, New Jersey: Princeton University Press, 1999, pp. 14-18.
-
[2] J. Cohen, P. Cohen, S. G. West dan L. S. Aiken, Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences 3rd Edition, Mahwah - New Jersey: Lawrence Earlbaum Associates, 2003, pp. 88.
-
[3] B. N. Taylor dan C. E. Kuyatt, NIST Technical Note 1297 : Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results, Washington: U.S. Government Printing Office, 1994, pp. 5- 8.
-
[4] R. Wicklin, “Coverage probability of confidence intervals: A simulation approach,” 2016. Available from: https://blogs.sas.com/content/iml/2016/09/08/coverage-probability-confidence-intervals.html,
diakses 10 Oktober 2019.
-
[5] Bureau of Indian Standards, “Accuracy (Trueness and Precision) of Measurement Methods and Results (IS 15393-6),” October 2003. Available from:
https://law.resource.org/pub/in/bis/S01/is.15393.6.2003.pdf, diakses 30 September 2019.
-
[6] A.-N. Spiess dan N. Neumeyer, “An Evaluation of R² as An Inadequate Measure for Nonlinear Models in Pharmacological and Biochemical Research: A Monte Carlo Approach,” BMC Pharmacology, vol. 10(6), 2010, pp. 1-10.
-
[7] J. Frost, “Standard Error of the Regression vs. R-squared,” 2017. Available from:
https://statisticsbyjim.com/regression/standard-error-regression-vs-r-squared, diakses 26 September 2019.
-
[8] Bureau of Indians Standard, “Accuracy (Trueness and Precision) of Measurement Methods and Results (IS 15393-1),” September 2003. Available from:
https://law.resource.org/pub/in/bis/S01/is.15393.1.2003.pdf, diakses 15 June 2020].
-
[9] J. J. Cahir, “Weather Forecasting,” 2019. Available from:
https://www.britannica.com/science/weather-forecasting/Long-range-forecasting, diakses 23
September 2019.
-
[10] D. Markucic, “How to Determine Repeatability and Reproducibility (R&R),” dalam 3rd EuropeanAmerican Workshop on NDE Reliability, Berlin, 2002.
-
[11] S. Gregoire, “Repeatability Reproducibility with A Standard Method ISO 5725-2,” dalam 7th ISTA Seminar on Statistics, Hohenheim, 2005.
-
[12] P. Assam Nkouibert, K. Mintiens, K. Knapen, Y. Van de Stede dan G. Molenberghs, “Estimating Precision, Repeatability, and Reproducibility From Gaussian and Non-Gaussian Data: A Mixed Models Approach,” Journal of Applied Statistics, vol. 37(10), 2010, pp. 18-20.
-
[13] D. Groselj, “Guidance on Instrumentation for Calibration Laboratories Including RICs,” Geneva, 2010.
-
[14] J. Frost, “Curve Fitting using Linear and Nonlinear Regression,” 2017. Available from: https://statisticsbyjim.com/regression/curve-fitting-linear-nonlinear-regression, diakses 26
September 2019.
SINTA 4 Accreditation Starting on Volume 19 No. 2, 2018
11
Discussion and feedback