The Classification of Primitive-Shaped Patterns by Using Principal Component Analysis Method

The Classification of Primitive-Shaped Patterns by Using Principal Component Analysis ……..

(I Gusti Agung Widagda, dkk)

Klasifikasi Pola Berbentuk Primitif dengan Menggunakan Metode Principal Component Analysis (PCA)

The Classification of Primitive-Shaped Patterns by Using Principal Component Analysis Method

I Gusti Agung Widagda¹*, Hery Suyanto²

^{1, 2}Program Studi Fisika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana, Jl. Kampus Bukit Jimbaran, Bali, 80361

Email: *igawidagda@unud.ac.id; hery@unud.ac.id

Abstrak – Pengenalan atau klasifikasi pola merupakan masalah utama dalam sistem penginderaan komputer (computer vision). Banyak metode telah diaplikasikan seperti: invarian momen, Jaringan Syaraf Tiruan (JST), K-mean, Support Vector Machine (SVM) dan lain-lain. Metode-metode ini memiliki beberapa kelemahan. Metode invarian momen sangat rentan terhadap noise. Metode JST memerlukan waktu komputasi yang lama (terutama JST banyak lapis) selama proses pelatihan. Disamping itu, dimensi ciri (feature) yang dihasilkan dari metode tersebut relatif tinggi sehingga memerlukan ruang penyimpanan (memori) yang besar. Selain itu, hal ini berpengaruh pada waktu komputasi yang lama ketika proses pengujian dilaksanakan. Berdasarkan pada fakta tersebut, dalam penelitian ini dipergunakan metode yang bisa mengurangi dimensi ciri yaitu metode Principal Component Analysis (PCA). Dalam metode PCA ini dimensi citra sampel dikonversi menjadi principal component (facespace), yang dimensinya jauh lebih kecil dari dimensi citra sampel itu sendiri. Hasil penelitian yang kami lakukan menunjukkan bahwa metode PCA sangat efektif dalam melakukan proses klasifikasi pola. Hal ini bisa terindikasi dari nilai Predictive Accuracy, Precision dan Recall yang relatif tinggi (mendekati 1) sedangkan FP Rate yang rendah (mendekati 0). Selain itu, lokasi koordinat titik (FP Rate, TP Rate) pada ROC graphs terletak pada wilayah kiri atas (mendekati wilayah classifier sempurna).

Kata kunci: principal component, pola primitif, PCA, keakuratan prediksi, computer vision

Abstract – The recognition or classification of patterns is a major problem in computer vision. Many methods have been applied such as: moment invariant, Artificial Neural Networks (ANN), K-mean, Support Vector Machine (SVM) and others. These methods have a few limitations. The moment invariant fashion is highly vulnerable to noise. ANN methods require a long computing time (especially multilayer ANN) during the training process. On the other hand, the dimensions of the features generated from the methods are relatively high, which requires large storage space (memory). In addition, this leads to the long computing time when the testing process is carried out. Based on these facts, this research makes use of methods that being able to reduce the feature dimensions, namely the Principal Component Analysis (PCA). In the PCA method the dimensions of the sample image are converted to principal components (face space), whose dimensions are much smaller than the dimensions of the sample image itself. Our works exhibit that the PCA method is highly effective in carrying out the pattern classification process. This can be indicated by the relatively high values of Predictive Accuracy, Precision and Recall (close to 1) while the FP Rate is low (close to 0). Moreover, the location of the point coordinates (FP Rate, TP Rate) in ROC graphs is fallen in the upper left region (approaching the perfect classifier region).

Key words: principal component, primitive pattern, PCA, Predictive Accuracy, computer vision

• 1.    Pendahuluan

Pengenalan atau pengklasifikasian pola merupakan bidang kajian di dalam sistem penginderaan komputer (Computer Vision). Proses klasifikasi pola dilakukan atas dasar persamaan (similarity) atau perbedaan (diversity) ciri (feature) pada pola. Klasifikasi pola, yang sangat mudah dilakukan oleh mata manusia tapi sulit bagi mesin (komputer), sudah lama menjadi pusat perhatian penelitian di bidang komputer dan menjadi komponen yang sangat penting dari berbagai sistem klasifikasi berbasis mesin (machine-based). Beberapa metode yang telah dipakai dalam penelitian yang terkait dengan pengenalan atau klasifikasi pola yaitu: metode invarian momen (moment invariant) dan Jaringan Syaraf Tiruan (JST).

Selain itu ada juga metode berdasarkan pada transformasi Wavelet, K-mean, Support Vector Machine (SVM), dan lain-lain. Metode momen invarian mengandalkan ciri citra (yaitu momen) yang tidak bergantung pada perubahan geometri obyek yang disebabkan oleh operasi: translasi, rotasi dan skala. Beberapa penelitian yang telah mengimplementasikan metode invarian momen antara lain: [1-4]. Kelemahan dari metode invarian momen yaitu rentan terhadap noise. Semakin tinggi orde dari momen invarian maka sangat rentan terhadap noise [5]. Di sisi lain, proses klasifikasi dengan metode JST bergantung secara garis besar atas ciri bobot (weight) dan/atau bias yang dihasilkan selama proses pelatihan (training). Ciri bobot ini selanjutnya dipakai pada proses klasifikasi atau pengujian (testing). Metode JST telah dipakai untuk pengenalan pola dalam penelitian [6-7]. Dari hasil penelitian ini secara eksplisit dapat dilihat bahwa metode JST bisa mengenali pola yang mengandung noise. Jadi metode JST memiliki kelebihan jika dibandingkan dengan metode momen invarian dalam menangani pola yang mengandung cacat atau noise. Ukuran atau dimensi dari data ciri yang dihasilkan metode JST maupun momen invarian biasanya besar sehingga berdampak pada waktu komputasi yang lama serta memerlukan ruang penyimpanan atau memori yang relatif besar. Berdasarkan fakta-fakta yang telah diuraikan diatas maka dalam penelitian ini dipakai metode alternatif yaitu Principal Component Analysis (PCA). PCA merupakan metode statistik yang dipakai untuk mengurangi dimensi variabel ciri dari citra sampel. Di dalam metode ini, setiap citra sampel direpresentasikan dengan principal component (facespace) yang ukuran dimensinya lebih kecil dari dimensi citra sampel tersebut. Facespace ini diperoleh dari perhitungan rata-rata (mean) dan variance/covariance citra sampel. Proses pengklasifikasian dilakukan dengan menghitung jarak (misal: jarak Euclidien) antara ciri (facespace) sampel citra pelatihan dan ciri (facespace) sampel uji. Penurunan ukuran dimensi ini berdampak pada peningkatan kecepatan komputasi ketika proses klasifikasi atau pengenalan pola dilakukan. Metode PCA ini sudah dipakai dalam beberapa penelitian untuk mendeteksi atau mengenali pola (seperti: wajah, sidik jari) [8-10].

• 2.    Landasan Teori

  • 2.1    Gambar dan tabel

PCA adalah metode statistik yang sudah dipakai dalam berbagai bidang seperti pengenalan pola, penginderaan jauh (remote sensing), kompresi citra dan lain-lain. Teknik ini biasanya dipakai untuk mengenali pola pada data atau sampel berdimensi tinggi dan menyatakan data tersebut dengan cara sedemikian rupa sehingga persamaaan dan perbedaan yang ada dalam data tersebut dapat ditentukan. Pemakaian PCA biasanya mempertimbangkan hubungan atau korelasi dari sampel data. Jika kita memiliki data atau vektor ciri (feature vector) dengan tingkat korelasi yang tinggi maka kita bisa mempertimbangkan untuk memakai metode PCA untuk mendekati vektor ciri tersebut, tapi dengan jumlah ukuran dimensi yang lebih rendah atau sedikit. PCA yang diimplementasikan pada kumpulan data yang memiliki korelasi yang kuat maka hasilnya akan lebih maksimal dibandingkan pada data dengan korelasi lemah. Dengan kata lain, semakin kuat tingkat korelasi dari data atau sampel maka metode PCA akan memberikan hasil yang semakin efektif. Sebagai contoh misalkan ada M orang anak yang ingin kita nilai perkembangan fisiknya. Pada masing-masing anak kita mencatat N buah variabel seperti umur, tinggi, berat, ukuran pinggang, panjang lengan, lingkar leher, dan lain-lain. Secara umum variabel tersebut saling tergantung atau berkorelasi satu sama lain. Anak yang umurnya lebih tua biasanya memiliki badan yang lebih tinggi, anak yang lebih tinggi umumnya memiliki berat badan yang lebih berat, anak yang lebih berat memiliki ukuran pinggang yang lebih besar, dan seterusnya. Jadi harus ada tingkat korelasi dari vektor data agar metode PCA bisa bermanfaat [11].

Jika N variabel yang diukur dinyatakan dengan vektor ciri yaitu:

x ,x ,...x

N

dan tiap-tiap vektor tersebut memiliki M elemen (entry) yaitu: x1(1), x1(2), x1(3),... x1(M) x2(1),x2(2),x2(3),...x2(M)

xN(1), xN(2), xN(3),...xN(M)

N vektor ciri membentuk matrik dengan ukuran M x N yaitu:

X = [x₁, x₂,...x_N]                                                                                       1)

Tujuan PCA yaitu untuk menentukan matrik [12]

Y =^[ >1^, y 2^,... yN^]

Sehingga

Y = XR

dimana kolom-kolom dari matrik Y adalah saling tegak lurus atau orthogonal. R adalah eigen vector yang akan kita bahas selanjutnya.

Prosedur atau cara untuk menentukan PCA dari suatu kumpulan data penelitian yaitu [13]:

2)

3)

1.

2.

3.

4.

5.

Tentukan vektor ciri, x ,x ...x . Vektor ciri ini selanjutnya dinyatakan dalam bentuk matrik x yaitu:

x = [Xi, x 2,...Xn ]

dimana tiap kolom dari matrik x tersusun dari vektor ciri xi.

Tentukan nilai rata-rata (mean) dari masing-masing vektor ciri, x , yaitu:

M

Xi = — Xx (j)

ⁱ M⅛

Tentukan nilai rata-rata nol (zero mean) ϕi, dengan mengurangkan nilai rata-rata, x , dari setiap elemen dari vektor ciri yang bersesuaian xi

^φi = X- ^x

dimana i = 1, 2, …N

Vektor zero mean ini dinyatakan dalam bentuk matrik ϕ yait

^φ = ^φ1^,φ2,.∙^φN ]

dimana tiap kolom dari matrik ϕ tersusun dari vektor zero mean ϕi.

Hitung matrik kovarian C(k,l)

M

C^{(k, l}) = ∑ ^(xk ⁽i) - ^Xk ^)(Xl⁽ⁱ) ^{- x}I)

i=1

dimana k = 1, 2, … M dan l = 1, 2, … M

Atau jika dinyatakan dalam bentuk matrik C, yaitu perkalian matrik ϕ^T dengan ϕ:

C = ΦTΦ

Hitung eigen vector dan eigen value dari matrik kovarian C (k,l) dengan persamaan [14]: Cu = λu

dimana u, λ merupakan eigen vector dan eigen value, secara berurutan. Persamaan (10) dapat diselesaikan dengan:

λu - Cu = 0

(λI - C )u = 0

det(λI - C ) = 0

Dengan menyelesaikan persamaan (12) ini maka akan didapatkan beberapa eigen value (λ) yaitu:

4)

5)

6)

7)

8)

9)

10)

11)

12)

• ₁,    ₂,... _M

Selanjutnya eigen value tersebut diurutkan dari nilai terbesar ke terkecil (descending). Eigen value yang terurut ini kemudian dipakai untuk menentukan eigen vector berdasarkan persamaan (11) yaitu:

u₁,u₂,...u_M

Selanjutnya nilai eigen vector ini dipakai untuk membentuk matrik transformasi U: U = [u₁, u 2,...Um ]

13)

6.

Tentukan komponen prinsip (principal component) Yi dengan mentransformasikan nilai rata-rata ϕi (langkah 3) dengan eigen vector ui:

Y = ^uφ

14)

15)

Selanjutnya vektor principal component ini dapat dinyatakan dalam bentuk matrik Y yaitu:

Y = [Y Y2,...Yn ]

• 7.    Tentukan vektor ciri baru Zi dengan mengalikan nilai principal component Yi dengan zero mean ϕi:

Zi= Yφ_l                                                                            16)

Selanjutnya vektor Zi ini dapat dinyatakan dalam bentuk matrik Z yaitu:

Z = [ Z1, Z 2,... Zn ]

17)

Matrik Z yang ditentukan dengan persamaan (17) ini merepresentasikan vektor ciri pola baru yang akan dipakai dalam proses pengenalan atau klasifikasi. Dimensi dari matrik ciri Z ini biasanya lebih kecil dari matrik ciri pola original pada persamaan (5). Matrik Z ini sering dikenal dengan nama matrik Facespace. Terkait dengan kasus pengenalan atau klasifikasi pola maka prosedur atau langkah (1-7) yang telah diuraikan sebelumnya merupakan proses pelatihan (training). Tahapan selanjutnya adalah proses pengujian (testing), langkah-langkahnya yaitu:

• 1.    Tentukan vektor ciri untuk sampel uji, x ,x ...x . Diasumsikan ada N sampel testing yaitu:

x = [x₁, x₂,... x_N ]

18)

19)

dimana tiap kolom dari matrik x tersusun dari vektor ciri xi.

• 2.    Tentukan nilai rata-rata (mean) dari masing-masing vektor ciri, x , yaitu:

M

x = — Vx (j) i M⅛ ⁱ

• 3.    Tentukan nilai rata-rata nol (zero mean) ϕi, dengan mengurangkan nilai rata-rata, x , dari setiap

elemen dari vektor ciri yang bersesuaian xi

φ_i = x_i - x_i20)

dimana i = 1, 2, …N

Vektor zero mean ini dinyatakan dalam bentuk matrik ϕ yaitu:

^φ = [^φ1^,φ2^,..^φN ]

dimana tiap kolom dari matrik ϕ tersusun dari vektor zero mean ϕi.

• 4.    Tentukan komponen prinsip (principal component) Yi dengan mentransforma- sikan nilai rata-rata ϕi (langkah 3) dengan eigen vector ui:

Y₁ = uφ_l

Selanjutnya vektor principal compo-nent ini dapat dinyatakan dalam bentuk matrik Y yaitu:

Y = Y Y2,...Yn ]

Catatan: Eigen vector yang dipakai disini adalah eigen vector yang diperoleh dari proses pelatihan

• 5.    Tentukan vektor ciri baru Zi dengan mengalikan nilai principal component Yi dengan zero mean ϕi:

Zi= YΦi24)

Selanjutnya vektor Zi ini dapat dinyatakan dalam bentuk matrik Z yaitu:

Z = [ Z ι, Z 2,... Zn ]

• 3.    Metode Penelitian

Penelitian ini dilakukan pada komputer dengan processor core i3 2.30 GHz, 4 GB RAM dengan sistem operasi Windows 10. Program aplikasi komputer untuk mengimplementasikan kode program yaitu Matlab versi 9.2.0.538062 (R2017a). Secara garis besar, alur dalam penelitian ini meliputi dua bagian yaitu: persiapan data penelitian (pelatihan, uji), perancangan diagram blok. Masing-masing alur tersebut akan diuraikan dalam sub bab berikut ini.

• 3.1    Data Penelitian

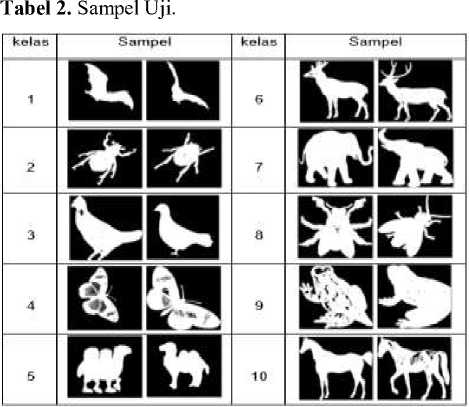
Data atau sampel yang dipakai dalam penelitian ini sebanyak 50 sampel citra berupa pola primitif dari beberapa jenis binatang seperti diperlihatkan pada Tabel 1. Sampel ini menyerupai citra siluet (silhouette) dari binatang. Masing-masing citra sampel berukuran 300 x 300 pixel. Sampel ini dibagi menjadi dua bagian yaitu: sampel pelatihan (30) dan sampel uji (20). Sampel ini dikatagorikan menjadi 10 kelas yaitu: kelelawar (1), kumbang (2), burung (3), kupu-kupu (4), onta (5), kijang (6), gajah (7), lalat (8), kodok (9) dan kuda (10). Sampel citra pelatihan dan sampel citra uji diperlihatkan, secara berurutan, dalam Tabel 1 dan Tabel 2.

Tabel 1. Sampel Pelatihan.

• 3.2    Perancangan Diagram Blok

Secara umum perancangan aplikasi klasifikasi dengan metode PCA terdiri dari dua bagian yaitu: pelatihan dan pengujian. Ada pun diagram blok dari kedua bagian tersebut digambarkan secara berturut-turut dalam Gambar 1 dan Gambar 2.

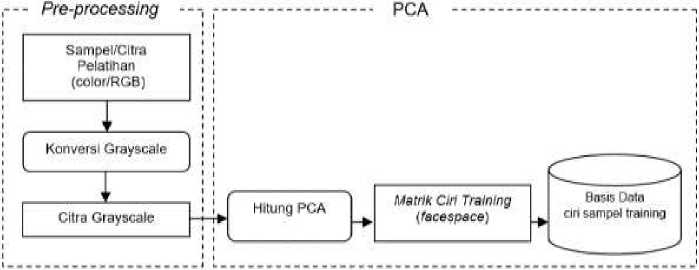
Gambar 1. Diagram blok proses pelatihan.

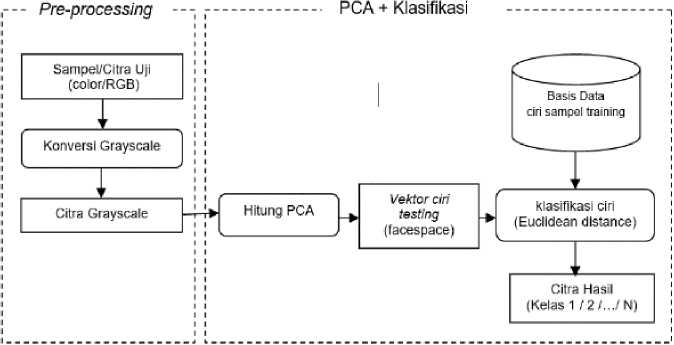
Gambar 2. Diagram blok proses pengujian.

• 4.    Metode Penelitian

  • 4.1    Hasil

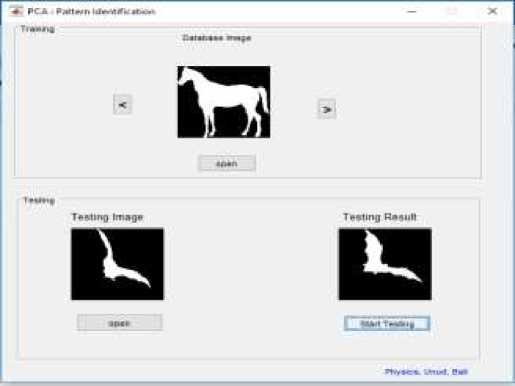
Hasil yang diperoleh dari penelitian ini berupa program aplikasi untuk mengklasifikasi pola primitif binatang dengan metoda PCA. Program ini terdiri dari dua bagian yaitu Training dan Testing seperti diperlihatkan pada Gambar 3.

Bagian Training (atas) dari Gambar 3 berfungsi untuk melakukan proses pelatihan, yang berguna untuk menghitung data ciri (feature) dari sampel citra pelatihan. Data ciri ini berupa facespace yang diturunkan dari principal component yang selanjutnya disimpan dalam database ciri. Sedangkan bagian Testing (bawah) berfungsi untuk melakukan proses klasifikasi dari citra sampel uji (bawah kiri). Klasifikasi didasarkan atas nilai kesamaan (jarak Euclidien) ciri citra uji dengan ciri citra yang tersimpan dalam database. Citra yang memiliki nilai kesamaan tertinggi (jarak Euclidien terkecil) dianggap sebagai citra hasil klasifikasi (bawah kanan). Citra hasil klasifikasi ditampilkan di bawah kanan. Hasil uji selengkapnya dari 20 sampel uji ditunjukkan pada Tabel 3.

Sampel uji pada Tabel 3 merupakan citra yang berbeda dengan sampel pelatihan. Sampel ini merupakan sampel baru dan tidak pernah dipakai selama proses pelatihan (unseen sample). Dari hasil klasifikasi dapat dilihat, citra uji ini sebagian besar bisa diklasifikasi dengan tepat oleh metode PCA ini. Hasil klasifikasi dalam Tabel 2 memperlihatkan beberapa sampel diklasifikasikan dengan salah (ditandai dengan kelas hasil uji berwarna merah) seperti: sampel kelas 3 (burung) diklasifikasikan sebagai kelas 1 (kelelawar), sampel kelas 4 (kupu-kupu) diklasifikasikan sebagai kelas 1 (kelelawar), sampel kelas 5 (onta) diklasifikasikan sebagai kelas 3 (burung), serta sampel kelas 6 (kijang) diklasifikasikan sebagai kelas 3 (burung). Selain sampel yang disebutkan diatas semuanya diklasifikasikan dengan tepat.

• 4.2    Evaluasi Kinerja PCA

Dari data hasil pengujian selanjutnya dilakukan proses evaluasi untuk menilai seberapa baik metode PCA ini. Beberapa metrik atau ukuran yang dipakai untuk menilai kinerja dari metode PCA yaitu: Keakuratan Prediksi (Predictive Accuracy), Precision, Recall, False Positive Rate dan ROC graphs. Suatu metode pengklasifikasi (classifier) dikatakan relatif baik jika menghasilkan nilai Predictive Accuracy, Precision dan Recall semuanya mendekati 1, namun nilai False Positif Rate (FP Rate) mendekati 0. Menurut Bramer (2013) [15], jika nilai ketiga metrik (Predictive Accuracy, Precision, Recall) sama dengan 1, dan nilai FP Rate sama dengan nol, maka metode pengklasifikasi tersebut dikatakan sempurna (perfect classifier). Untuk menentukan nilai dari keempat metrik tersebut biasanya diawali dengan menentukan matrik konfusi (confusion matrix). Matrik ini merupakan matrik dua dimensi dengan ukuran n x n, dimana n menunjukkan jumlah kelas atau label yang dipakai. Dalam penelitian kita memakai 10 kelas yaitu: kelelawar (1), kumbang (2), burung (3), kupu-kupu (4), onta (5), kijang (6), gajah (7), lalat (8), kodok (9), kuda (10). Jumlah sampel uji tiap kelas yaitu 2, sehingga total sampel uji yaitu 2 x 10 = 20.

• a)    Confusion Matrix

Bentuk Confusion matrix dari hasil pengenalan atau klasifikasi 20 sampel uji yang dipakai dalam penelitian ini diperlihatkan pada Tabel 4.

Elemen diagonal confusion matrix (Tabel 4) yaitu elemen (1,1), (2,2), ... (10,10) merupakan sampel uji yang diklasifikasikan dengan benar, sedangkan elemen lain adalah sampel yang klasifikasinya salah. Arti dari beberapa elemen matrik yaitu:

• -    elemen (1,1) = 2, artinya dari 2 sampel uji kelas 1 (kelelawar) semuanya diklasifikasikan sebagai kelas 1 (kelelawar).

• -  elemen (4,4) = 1 dan elemen (4,1) = 1, artinya dari 2 sampel uji kelas 4 (kupu-kupu) ada 1 sampel

kelas 4 (kupu-kupu) diklasifikasikan sebagai kelas 4 (kupu-kupu) serta 1 sampel kelas 4 (kupu-

kupu) diklasifikasikan sebagai kelas 1 (kelelawar).

• -  elemen (5,5) = 1 dan elemen (5,3) = 1, artinya dari 2 sampel uji kelas 5 (onta) ada 1 sampel kelas 5

(onta) diklasifikasikan sebagai kelas 5 (onta) serta 1 sampel kelas 5 (onta) diklasifikasikan sebagai

kelas 3 (burung).

• -    elemen (6,6) = 1 dan elemen (6,3) = 1, artinya dari 2 sampel uji kelas 6 (kijang) ada 1 sampel kelas 6 (kijang) diklasifikasikan sebagai kelas 6 (kijang) dan 1 sampel kelas 6 (kijang) diklasifikasikan sebagai kelas 3 (burung).

Confusion matrix 10 kelas ini dapat disederhanakan menjadi confusion matrix 2 kelas atau biner [15], dengan menganggap kelas 1 (kelelawar) sebagai positif (+) dan kelas lainnya (2, 3, …10) sebagai negatif (-), seperti diperlihatkan Tabel 5.

Gambar 3. Program aplikasi klasifikasi bentuk primitive dengan metode PCA.

Tabel 3. Sampel uji.

Tabel 4. Confusion Matrix 20 sampel uji.

Predicted Class

	Keldnwai (II	Kuiiibiing (J)	Buniog (⅛	Kupu-kupu (4)	Onta (S)	Kijaag (6)	Gajah CT⅛	Lalal 18)	Kodok W	Kuda (IO)
KelelawM < 1)	2	O	O	U	O	O	O	O	O	O
KjtUt-SUlglZl	0	2	O	O	O	O	O	O	O	O
BuntngiJi	1	O	J	O	O	O	Q	O	O	O
Kupu-kupu (4)	1	O	O	1	O	O	O	O	O	O
Onta <5)	O	O	1	O	1	(1	6	O	O	O
KjjHue ∣6∣	O	O	1	O	O	I	Q	O	O	O
OaJah (7)	C'	O	O	O	O	0	2	O	O	O
Lalat (8)	O	O	O	O	O	O	O	2	O	O
Kodok 19)	O	O	O	O	O	O	O	O	2	O
Kuda (10)	O	O	O	O	O	O	O	O	O	2

Tabel 5. Confusion matrix biner 20 sampel uji.

Predicted class

	Positive (+)	Negative (∙)
Positive (+)	2 (TP)	O(FN)
Negative (∙)	2 (FP)	16(TN)

dimana,

TP (True Positive) = jumlah kelas positif diklasifikasikan sebagai kelas positif TN (True Negative) = jumlah kelas negatif diklasifikasikan sebagai kelas negatif FP (False Positive) = jumlah kelas negatif diklasifikasikan sebagai kelas positif FN (False Negative) = jumlah kelas positif diklasifikasikan sebagai kelas negatif.

• b)    Predictive Accuracy

Predictive accuracy atau disingkat accuracy merupakan ukuran yang menyatakan perbandingan antara banyaknya sampel yang diklasifikasikan dengan benar dengan jumlah seluruh sampel, yang dinyatakan dengan persamaan berikut ini [16-17]:

accuracy =

TP + TN

TP + TN + FP + FN

26)

=   ²⁺¹⁶   = 18=o,9

2 +16 + 2 + 0  20   ^,

• c)    Precision

Precision adalah metrik yang menyatakan perbandingan antara banyaknya sampel yang diklasifikasikan sebagai positif yang benar-benar positif:

TP precision =

27)

TP + FP

2

2 + 2

2

4

= 0,5

• d)    Recall

Recall atau sering disebut True Positive Rate (TP Rate) adalah ukuran banyaknya sampel positif yang diklasifikasikan dengan benar sebagai positif:

recall =

TP

TP + FN

28)

2

2 + 0

2 = 1

2

• e)    False Positive Rate

False Positive Rate (FP Rate) atau sering disebut False Alarm Rate (FAR) adalah ukuran banyaknya

sampel negatif yang diklasifikasikan dengan salah sebagai positif:

FP Rate =

FP

TN + FP

29)

2

16+2

2

18

= 0,11

Dari hasil perhitungan didapatkan nilai Predictive Accuracy (0,9), Precision (0,5) dan Recall (1) semuanya mendekati/sama dengan 1. Demikian juga nilai FP Rate (0,11) mendekati 0. Sehingga kita bisa menyatakan metode PCA ini merupakan metode yang relatif baik untuk mengenali atau mengklasifikasi pola atau sampel berbentuk primitif.

• f)    ROC graphs

Receiver Operating Characteristic (ROC) graphs adalah grafik dimana sumbu horisontal menyatakan nilai FP Rate dan sumbu vertikal merupakan TP Rate. Tiap titik dalam ROC graphs dinyatakan dengan pasangan koordinat (x, y) dimana x dan y, secara berurutan, merepresentasikan FP Rate dan TP Rate. Dari hasil perhitungan sebelumnya didapatkan nilai FP Rate (0,11) dan TP Rate (1). Koordinat titik (0,11, 1) pada ROC Graphs diperlihatkan pada Gambar 4.

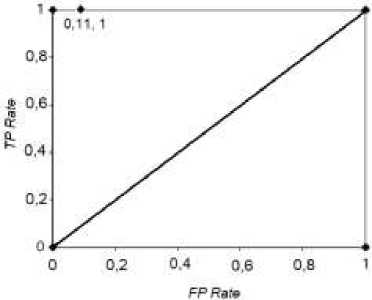
Gambar 4. Receiver Operating Characteristic (ROC) graphs.

Suatu metode pengklasifikasi (classifier) dikatagorikan baik jika koordinat titik pasangan (FP Rate, TP Rate) terletak di sebelah kiri atas ROC graphs. Titik (0,1) merupakan classifier terbaik (sempurna) dan titik (1,0) merupakan classifier terburuk [15]. Dari Gambar 2 dapat dilihat secara relatif koordinat titik (0,11, 1) terletak di sebelah kiri atas, hampir mendekati titik (0,1) untuk classifier sempurna. Sehingga dapat disimpulkan bahwa metode PCA yang dipakai dalam penelitian ini dapat dikatagorikan sebagai metode yang baik.

• 5.    Kesimpulan

Dari hasil penelitian yang telah dilakukan serta pembahasan yang telah diuraikan di atas maka dapat disimpulkan bahwa metode PCA merupakan metode pengklasifikasi pola (bentuk primitif) yang baik, secara kuantitatif terlihat dari nilai Predictive Accuracy, Precision dan Recall yang tinggi (mendekati 1), serta nilai FP Rate yang rendah (mendekati 0). Serta lokasi titik pada ROC graphs terletak pada wilayah kiri atas (mendekati wilayah sempurna).

Ucapan Terima Kasih

Penulis menyampaikan terimakasih kepada semua pihak yang telah berperan serta dalam penyelesaian jurnal ini.

Pustaka

• [1]    Hu Ming-Kuei. 1962. Visual Pattern Recognition by Moment Invariants. IRE Transaction on Information Theory.

• [2]    Jan Flusser. 2005. Moment Invariants in Image Analysis. World Academy of Science, Engineering and Technology.

• [3]    Yaser S. Abu-Mustafa and Demetri Psaltis. 1984. Recognitive Aspects of Moment Invariants. IEEE

Transactions on Pattern Analysis and Machine Intelligence. Vol. PAMI-6. NO. 6.

• [4]    Zhihu Huang and Jinsong Leng. 2010. Analysis of Hu’s Moment Invariants on Image Scaling and Rotation. Proceedings of 2nd International Conference on Computer Engineering and Technology (ICCET). pp. 476-480. Chengdu. China. IEEE.

• [5]    Cho-huak Teh and Roland T. Chin. 1988. On Image Analysis by the Methods of Moments, IEEE Transactions on Pattern Analysis and machine Intelligence. vol. 10. pp. 496-513.

• [6]    Lazimul Limnd T. P and Binoy D.L. 2017. Fingerprint Liveness Detection using Convolutional Neural Network and Fingerprint Image Enhancement. International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS).

• [7]    Liu Yong-xial, Qi Jin and Xie Rue. 2010. A New Detection Method of Singular Points of Fingerprints Based on Neural Network, IEEE.

• [8]    Alaa Eleyan and Hasan Demirel. 2007. Face Recognition using Multiresolution PCA. IEEE International Symposium on Signal Processing and Information Technology. vol. 10. pp. 496-513.

• [9]    Aruna Kumari P. and Jaya Suma G. 2016. An Experimental Study of Feature Reduction Using PCA in Multi-Biometric Systems Based on Feature Level Fusion. IEEE International Conference on Advances in Electrical, Electronic and System Engineering.

• [10]    Xunqiang Tao, Xin Yangy, Yali Zang, Xiaofei Jia and Jie Tian. 2012. A Novel Measure of Fingerprint Image Quality Using Principal Component Analysis (PCA). IEEE.

• [11]    Solomon, Chris and Breckon, Toby. 2011. Fundamentals of Digital Image Processing: A Practical Approach with Examples in Matlab. Wiley-Blackwell. USA.

• [12]    Sundarajan, D. 2017. Digital Image Processing. A Signal Processing and Algorithmic Approach. Springer Nature. Singapore.

• [13]    Petrou, Maria. and Petrou, Costas. 2010. Image Processing. The Fundamentals (second edition). John Wiley & Sons Ltd. UK.

• [14]    Anton, Howard. and Rorres, Chris. 2014. Elementary Linear Algebra: Applications Version. Wiley. USA.

• [15]    Bramer, M. 2013. Principles of Data Mining (second edition). Springer-Verlag. London.

• [16]    Aghdam, H.H. and Heravi, E.J. 2017. Guide to Convolutional Neural Networks. A Practical Application to Traffic-Sign Detection and Classification. Springer. Switzerland.

• [17]    Arif Wani, M., Bhat F.A., Afzal S. and Khan, A.I. 2020. Advance in Deep Learning. Springer Nature. Singapore.

21