PEMILIHAN MODEL TERBAIK DAN PERAMALAN JUMLAH KUNJUNGAN WISATAWAN MANCANEGARA (WISMAN) KE BALI TAHUN 2014

66 Jurnal Buletin Studi Ekonomi, Vol. 20 No. 1, Februari 2015

PEMILIHAN MODEL TERBAIK DAN PERAMALAN JUMLAH KUNJUNGAN WISATAWAN MANCANEGARA (WISMAN) KE BALI TAHUN 2014

Rukini¹

I Wayan Sukadana² Luh Gede Meydianawathi^{3 1}Biro Pusat Statistik

• ^2,3Jurusan Ekonomi Pembangunan, Fakultas Ekonomi dan Bisnis Universitas Udayana e-mail : [email protected]

Abstract : The Selection Of Best Model and Forecasting The Number Of Foreign Tourists Arrival At Bali In 2014. The number of foreign tourists visiting Bali according to figures Central Bureau of Statistics (BPS) recorded the highest in Indonesia, so it is interesting to observe, more specifically related to the prediction of the number of foreign tourists who will visit Bali at some future period. Forecasting method requires stationary data, there are some cases (intervention). In this case the Bali bombings make data on the number of tourist becomes stationary so it needs to be analyzed by comparing the existing forecasting methods. Two methods are applied in this study, which are: Intervention and ARIMA models. The models allow to solve the case of time series data that often not stationary. With the Box-Jenkins procedure and visually observing and forecasting the estimated results of these two methods. The results showed that the best model for the case that the number of tourist arrivals to Bali through Ngurah Rai airport is ARIMA model, which has the smallest value of AIC and RMSE.

Keywords: Bali bombing, ARIMA, intervention

Abstrak : Pemilihan Model Terbaik Dan Peramalan Jumlah Kunjungan WIsatawan Mancanegara (WISMAN) Ke Bali Tahun 2014. Jumlah wisatawan mancanegara yang berkunjung ke Bali menurut angka Badan Pusat Statistik (BPS) tercatat tertinggi di Indonesia, sehingga menarik untuk diamati, lebih khusus terkait dengan peramalan mengenai jumlah wisatawan mancanegara yang akan berkunjung ke Bali pada beberapa periode ke depan. Metode peramalan mensyaratkan data yang stationer, adanya beberapa kasus (intervensi) dalam hal ini kejadian bom Bali membuat data jumlah kunjungan wisatawan mancanegara yang berkunjung ke Bali menjadi tidak stasioner sehingga perlu dilakukan analisis dengan membandingkan metode peramalan yang ada. Dua metode diterapkan dalam penelitian ini yaitu: Model Intervensi dan ARIMA yang memungkinkan untuk mengatasi kasus data time series yang tidak stasioner. Dengan prosedur Box-Jenkins dan mengamati secara visual hasil taksiran maupun peramalan dari kedua metode ini. Hasil penelitian diperoleh bahwa model terbaik untuk kasus jumlah kunjungan wisatawan mancanegara yang berkunjung ke Bali melalui bandara Ngurah Rai adalah model ARIMA, dimana memiliki nilai AIC dan RMSE terkecil.

Kata kunci: bom Bali, ARIMA, intervensi

PENDAHULUAN

Pesona dan daya tarik yang dimiliki Pulau Dewata Bali sudah tidak diragukan lagi, keindahan tempat-tempat pariwisata di Bali sangat terkenal di Indonesia bahkan sampai mancanegara, dan menjadi tempat yang banyak diminati untuk dikunjungi wisatawan domestik maupun asing. Dari tahun ke tahun jumlah wisatawan yang berkunjung ke Pulau Dewata semakin meningkat. Tren yang menunjukkan keberhasilan industri pariwisata di Bali, hingga pada titik dimana tragedi bom Bali tahun 2002 dan bom

Bali tahun 2005 terjadi, adalah pukulan telak bagi industri pariwisata di Bali, Selain menelan korban jiwa, serangan teroris tersebut juga menyebabkan rusaknya citra Bali sebagai destinasi wisata yang aman dan nyaman di mata dunia internasional. Industri pariwisata yang baru mulai bangkit setelah serangan bom bali tahun 2002 harus kembali terpuruk dan mulai dari nol untuk kembali membangun kepercayaan dunia internasional. Dampaknya luar biasa, kunjungan wisatawan pasca tragedi menurun drastis, tentu saja merosotnya jumlah wisatawan mancanegara tersebut otomatis berdampak pada

menurunnya tingkat hunian kamar hotel (occupancy rate) hingga 40-50%, restoran dan pangsa pasar pariwisata.

Strategi sebagai upaya untuk meningkatkan jumlah kunjungan wisatawan ke Bali pasca bom Bali harus terus diupayakan, karena sektor pariwisata memiliki peranan penting dalam perekonomian khususnya Bali. Dunia pariwisata telah banyak memberikan konstribusinya terhadap kehidupan ekonomi. Peningkatan jumlah wisatawan yang tidak terduga menyebabkan kesulitan bagi para pelaku pariwisata di Bali untuk memberikan pelayanan terbaik bagi para wisatawan. Untuk mengatasi permasalahan tersebut maka diperlukan suatu proses peramalan jumlah kedatangan wisatawan, sehingga diharapkan dapat memberikan informasi mengenai perkiraan jumlah kedatangan wisatawan kepada para pelaku wisata untuk mempersiapkan operasional yang baik, dan juga menggali inovasi-inovasi dan strategi pemasaran yang baik. Terkait dengan strategi tentu tak lepas dari perencanaan. Data yang akurat dan up to date diperlukan untuk menyusun perencanaan, terkait dengan hal ini diharapkan bahwa angka jumlah kunjungan wisatawan akan meningkat, untuk itu diperlukan metode peramalan akan banyaknya jumlah wisatawan yang berkunjung di Bali pada beberapa periode waktu ke depan. Pada penelitian Rukini (2014), terdapat keterkaitan atau pengaruh secara signifikan antara jumlah wisatawan mancanegara yang datang ke Bali dengan tingkat inflasi Kota Denpasar.

Dengan demikian, analisis peramalan menjadi penting dan ketepatan akan analisis time series akan sgi meningkatkan sektor pariwisata yang dapat

menarik wisatawan untuk berkunjung ke Bali. Peramalan jumlah kunjungan wisatawan mancanegara yang masuk ke suatu negara sangat dibutuhkan bagi pelaku bisnis pariwisata, sehingga memodelkan data jumlah kunjungan wisatawan mancanegara perlu untuk dilakukan. Penelitian ini mencoba membandingkan ketepatan hasil peramalan dari dua model yakni Autoregresive Integrated Moving Avarage (ARIMA) dan Intervensi pada kasus peramalan jumlah wisatawan manca negara melalui Bandara Udara Ngurah Rai selama bulan Januari 2000-April 2014. Data dibagi dalam kelompok, yaitu in-sample dan out-sample. In-sample dari tahun 2000-2013, dan out sample yang akan digunakan untuk peramalan adalah Januari 2014 sampai dengan April 2014 serta mendapatkan ramalan jumlah wisatawan mancanegara yang datang ke Bali tahun 2014.

KAJIAN PUSTAKA

Metode ARIMA Box-Jenkins

Prosedur pembentukan model ARIMA meliputi beberapa tahapan yaitu identifikasi, estimasi, cek diagnosa dan peramalan. Model Box-Jenkins (ARIMA) dibagi ke dalam 3 kelompok, yaitu: model autoregressive (AR), moving average (MA), dan model campuran ARMA (autoregressive moving average) yang mempunyai karakteristik dari dua model pertama (Box and Jenkins, 1994).

Identifikasi

Identifikasi model ARIMA dapat dilakukan dengan melihat plot ACF (Autocorrelation fuction) dan plot PACF (Parsial Autocorrelation fuction)

Tabel 1.

Karakteristik ACF dan PACF yang Stasioner

Proses	ACF	PACF
Autoregressive orde p	Dies down	Cuts off setelah lag ke-p
Moving Average orde q	Cuts off setelah lag ke-q	Dies down
ARMA orde (p,q)	Dies down	Dies down

Sumber : Data diolah (2104)

Estimasi Parameter

Ada beberapa cara yang dapat digunakan untuk mendapatkan parameter-parameter model ARIMA (Wei, 2006), antara lain :

• a.    Metode Momen

• b.    Metode Maximum Likelihood

• c.    Metode OLS (Ordinary Least Squares)

Secara umum, misalkan δ adalah suatu parameter

pada model ARIMA (mencakup φ , θ dan µ ) dan

δˆ adalah nilai estimasi dari parameter tersebut, serta s.e (δ^ˆ) adalah standar error dari nilai taksiran δˆ maka uji signifikansi parameter dapat dilakukan

sebagai berikut:

Hipotesa:

H₀ : δ = 0

(parameter tidak signifikan)

H₁ : δ ≠ 0 (parameter signifikan)

ˆ

Statistik uji:       δ .................................(1)

^t

s.e(δ)

Daerah penolakan : Tolak H₀ jika 11 | > t_α/2; n - m atau menggunakan nilai p-value < artinya a parameter signifikan.

Pemeriksaan Diagnostik

Pemeriksaan diagnosis residual dari model, yaitu residual bersifat white noise juga berdistribusi normal. Pengujian asumsi white noise menggunakan uji Ljung-Box dengan hipotesis sebagai berikut: H₀ : ρ₁ = ρ₂ = ■■■ = pK = 0 (residual White Noise) H₁ :minimal ada satu pk ≠ 0(residual tidak White

Noise),

dengan k = 1,2,..., K

K

Statistik Uji: Q = n(n + 2) ∑ (n - k)^-1 p_k² ...........(2)

k=1

daerah penolakan: Tolak jika , dengan (orde ARMA) atau dengan menggunakan p-value < , artinya model tidak sesuai karena residual tidak memenuhi asumsi White Noise. Pengujian selanjutnya yaitu uji asumsi residual berdistribusi normal. Pengujian ini dilakukan dengan menggunakan Kolmogorov Smirnov. Hipotesis yang digunakan adalah :atau residual berdistribusi normal atau residual tidak berdistribusi normal

Statistik uji : D = sup | F_n (x) - F₀ (x) |....................3

dimana :          ^x

F₀ (x) = fungsi yang dihipotesiskan berdistribusi normal

F_n (x) = fungsi distribusi kumulatif dari data asal n = banyaknya residual

Nilai D_hitung dibandingkan dengan nilai pada tabel Kolmogorov-Smirnov dengan derajat bebas n . Daerah penolakan: Tolak H₀ jika Dhi_tung > D_a,n atau dapat menggunakan p-value. Jika p-value < berarti H₀ ditolak yang berarti residual tidak berdistribusi normal.

Pemilihan Model Terbaik

Untuk menentukan model terbaik dapat digunakan kriteria pemilihan model yang berdasarkan residual dan kesalahan peramalan (Wei, 2006). Adapun kriteria pemilihan model yang berdasarkan residual pada data in-sample menggunakan nilai AIC dan SBC. Sedangkan untuk pemilihan model berdasarkan kesalahan peramalan pada data out-sample menggunakan nilai RMSE.

dengan : AIC(mM)=n lnc^a2 + 2M...........................(4)

n = banyaknya residual

M = jumlah parameter di dalam model σˆ² = varians dari residual.

a

SBC(M = n ln σ2 + M ln n

RMSE = ¹ ∑ ee

n

l =1

dimana e_l =Z_n+1 -Z_n(l).....................................⁽⁵⁾

Prosedur Pembentukan Model Intervensi

Bentuk umum dari model intervensi adalah sebagai berikut (Wei, 2006):

k ωsj (B)     θ q ( B )             (6)

dimana: y^t ∑ δrj (b) ^{1 t +} φp (B) ^at

y_t = representasi dari deret output yang stasioner (variabel dependen)

I = variabel intervensi ke- j

j,t

ω_sj (B) = operator moving average order s j untuk variabel ke- j

δ_rj (B) = operator autoregresi order rj untuk variabel ke-j

θq (B) = operator moving average order q

φ_p(B) = operator autoregresi order p

a_t = nilai gangguan acak

Tahapan Pembentukan Model Intervensi

• a.    Identifikasi Bentuk Model

• -    Mempersiapkan data berdasarkan waktu-waktu intervensi

• -    Menentukan model ARIMA menggunakan prosedur Box-Jenkins

• -    Identifikasi order model intervensi

Dalam mengidentifikasi order pada model intervensi, ada dua metode yang dapat dilakukan yaitu :

• 1.    Metode Eksploratori dimana order didapatkan melalui suatu besaran statistik untuk mengeksplorasi kemungkinan order yang sesuai dengan melihat plot residual.

• 2.    Metode Konfirmatori, dimana order ditetapkan berdasarkan diskriptif data melalui plot time series pada setiap waktu dimana terjadi intervensi tersebut.

• b.    Estimasi Parameter Model Intervensi

• c.    Diagnosa Model Intervensi

METODE PENELITIAN

Sumber Data

Sumber data dari penelitian ini adalah data sekunder yang diperoleh dari Badan Pusat Statistik

Provinsi Bali, yakni jumlah kunjungan wisatawan mancanegara per bulan dari bandara internasional Ngurah Rai Denpasar dengan series data dari Januari 2000 hingga April 2014. Pada proses analisis, data akan dibagi menjadi dua bagian yaitu data training untuk pembentukan model dan data testing untuk validasi dan pemilihan model terbaik. Data periode Januari 2000 sampai dengan Desember 2013 digunakan sebagai data training (in-sample) dan data periode Januari 2014 sampai dengan April 2014 sebagai data testing (out-sample).

Secara umum ada dua variabel yang digunakan dalam penelitian ini, yaitu variabel respon (output) dan variabel prediktor (input). Variabel output yang menjadi fokus kajian penelitian adalah jumlah

wisatawan mancanegara yang berkunjung ke Bali yang diamati dalam periode bulan (y1). Sedangkan variabel input penelitian terdiri atas variabel intervensi kejadian bom bali 2002 (b1) dan bom bali 2005 (b2).

HASIL DAN PEMBAHASAN

Analisis ARIMA

Berdasarkan langkah-langkah prosedur Box-Jenkins diperoleh hasil sebagai berikut :

• a. Identifikasi Model

Langkah awal dalam metode ARIMA adalah dengan membuat plot time series data, sebagaimana dapat dilihat pada Gambar 1.

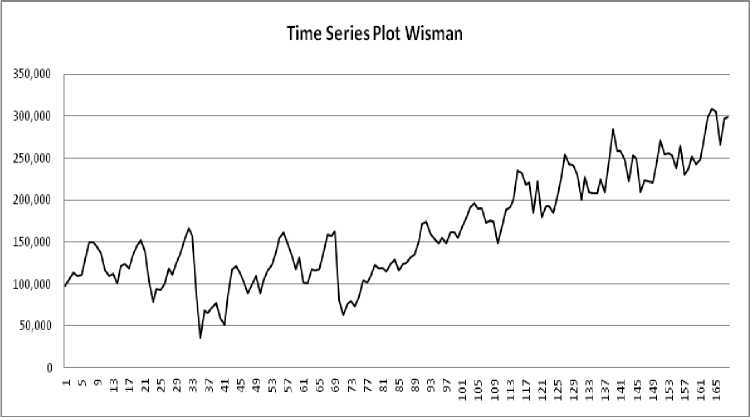
Gambar 1.

				Autoc		orrelations
Lag	Covariance	Correlation	-1	9 8	7	6 5 4	3 2	1	0 1 2 3 4 5 6	7	8 9 1	Std Error
0	4736100058	1.00000	|						|*************	**	*****|	0
1	4308387911	0.90969	|				.		|*************	**	***   |	0.076472
2	3913490806	0.82631	|				.		|*************	**	**     |	0.124606
3	3531225235	0.74560	|				.		|*************	**	|	0.153338
4	3144291696	0.66390	|			.			|*************		|	0.173247
5	2832788447	0.59813	|			.			|************		|	0.187536
6	2536947638	0.53566	|			.			|***********		|	0.198378
7	2281077922	0.48164	|			.			|**********		|	0.206664
8	2087121749	0.44068	|			.			|*********		|	0.213127
9	1981451706	0.41837	|			.			I ******** .		|	0.218390
10	1858236198	0.39236	|			.			|******* .		|	0.223028
11	1771040968	0.37395	|			.			I ******* |.		|	0.227029
12	1576624906	0.33290	|			.			|********.		|	0.230603
13	1220016832	0.25760	|			.			I ****** |.		|	0.233396
14	879020489	0.18560	|			.			I * * * * |.		|	0.235053
15	515711285	0.10889	|			.			I * * |.		|	0.235908
16	369786531	0.07808	|			.			I * * |.		|	0.236202
17	239331899	0.05053	|			.			|*            .		|	0.236353
18	114065626	0.02408	|			.			|                                    .		|	0.236416
19	61087458	0.01290	|			.			|                                    .		|	0.236430
20	107765439	0.02275	|			.			|                                    .		|	0.236435
21	197424750	0.04169	|			.			|*            .		|	0.236447
22	289782063	0.06119	|			.			|.		|	0.236490
23	364912242	0.07705	|			.			I * * |.		|	0.236583
24	398619089	0.08417	|			.			I * * |.		|	0.236730

Gambar 2. Plot ACF Jumlah Wisatawan Mancanegara

Gambar 2 menunjukkan plot ACF jumlah wisatawan mancanegara, dimana terlihat pola dies down yang lambat dan berulang pada periode ke-12. Hal ini mengindikasikan bahwa data belum stasioner dalam mean (rata-rata) dan adanya faktor musiman. Sehingga perlu dilakukan differencing 1 reguler kemudian di differencing musiman 12. Gambar 3 dan Gambar

• 4 menunjukkan plot ACF dan PACF data jumlah wisatawan mancanegara setelah differencing 1 reguler dan differencing musiman 12. Setelah dilakukan proses differencing, plot ACF memperlihatkan bahwa data telah stasioner dalam rata-rata. Melalui plot ACF dan PACF tersebut dapat diidentifikasi order model ARIMA yang sesuai untuk data jumlah wisatawan mancanegara

Autocorrelations

Lag -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1

0   |                      |********************|

• 1     |                          ****|    .|

• 2           |                                                        .        |        .|

• 3           |                                                        .        |        .|

• 4          |                                                        .        |        .|

• 5       |                                        .      |*   .|

• 6       |                                        .      |*   .|

• 7           |                                                        .        |        .|

• 8       |                                        . *|      .|

• 9       |                                        .      |*   .|

• 10      |                                   . *| .|

• 11     |                            . |***|

• 12    |            **********|   .|

Partial Autocorrelations

Lag -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1

• 1   |                           ***|    .|

• 2     |                                        .   *|      .|

• 3       |                                                        .        |        .|

• 4       |                                                        .        |        .|

• 5       |                                                        .        |        .|

• 6     |                                        .      |*   .|

• 7       |                                                        .        |        .|

• 8     |                                        .   *|      .|

• 9     |                                        .      |*   .|

• 10    |                                   .  *|     .|

• 11   |                            .    |***|

• 12   |            **********|   .|

Gambar 3

Plot ACF jumlah wisatawan mancanegara setelah differencing 1 reguler dan musiman 12

Gambar 4.

Plot PACF jumlah wisatawan mancanegara setelah differencing 1 reguler dan musiman 12

Dengan melihat pola PACF yang dies down dan ACF cut off di lag1 dan lag 12, maka dugaan model ARIMA yang terbentuk adalah model ARIMA (0,1,1)(0,1,1)¹² . Langkah selanjutnya adalah estimasi parameter dan diagnostik model deret input. Berdasarkan Tabel 2 Menunjukkan bahwa dengan

taraf signifikansi 5% parameter pada model ARIMA (0,1,1)(0,1,1)¹² mempunyai nilai p-value kurang dari α = 0, 05 maka H₀ ditolak yang berarti bahwa parameter model ARIMA (0,1,1)(0,1,1)¹² signifikan. Sehingga parameter dapat digunakan dalam model.

Tabel 2.

Estimasi dan Uji Signifikansi Parameter Model ARIMA (0,1,1)(0,1,1)¹²

Jumlah Wisatawan Mancanegara

Parameter            Estimasi	p-value                Keputusan
θ1               0,36555	<,0001                  Signifikan
θ12               0,80987	<,0001                  Signifikan
Sumber : Data diolah (2104)	Tabel 3

Hasil Uji White Noise Residual Model ARIMA(0,1,1)(0,1,1)¹²

Jumlah Wisatawan Mancanegara

Lag            Chi-Sqrt	DF          p-value         Keputusan
6                4,97 12               9,44 18               12,30 24               16,50 30              21,47	4            0,2899         White Noise 10            0,4905         White Noise 16            0,7228         White Noise 22            0,7905         White Noise 28            0,8050         White Noise

Berdasarkan Tabel 3 terlihat bahwa autokorelasi residual model ARIMA (0,1,1)(0,1,1)¹² menunjukkan nilai p-value yang lebih besar dari α = 0,05 artinya autokorelasi residual tidak signifikan atau tidak terdapat korelasi antar lag atau residual sudah white noise. Pengujian asumsi kenormalan dengan uji Kolmogorov-Smirnov

dengan taraf signifikansi 5 % memiliki nilai p-value kurang dari 0,05. Sehingga dapat disimpulkan bahwa residual belum memenuhi asumsi berdistribusi normal.

Ketidak normalan bisa disebabkan adanya data yang outlier, sehingga perlu di deteksi dan hasilnya diperoleh data outlier pada Tabel 5.

Tabel 4

Hasil Uji Normalitas Residual Model ARIMA (0,1,1)(0,1,1)¹²

Jumlah Wisatawan Mancanegara

Test	D_hitung       p-value                Keputusan
Kolmogorov-Smirnov	0,084061        0,0100         Tidak Berdistribusi Normal
Sumber : Data diolah (2104)	Tabel 5 Hasil Identifikasi 10 data outlier

Obs	Type	Estimate	Square	ChiSq
70	Shift	-60575.2	30,39	<,0001
34	Shift	-65617.3	34,30	<,0001
166	Additive	-36707.2	15,86	<,0001
146	Shift	-33700.8	10,78	0,0010
35	Additive	-27868.4	11,23	0,0008
22	Shift	-32573.8	11,82	0,0006
83	Shift	26479,4	8,60	0,0034
120	Additive	23780,9	9,34	0,0022
110	Additive	-23085,2	8,83	0,0030
40	Shift	-23566,5	7,12	0,0076

Sumber : Data diolah (2104)

Dengan melakukan estimasi dan uji signifikansi parameter dengan data outlier, hanya ada tiga data outlier yang signifikan seperti terlihat pada Tabel 6. Dengan taraf signifikansi 5% memiliki nilai p-value

kurang dari alpha 0,05 yang berarti parameter telah signifikan yang dapat dimasukkan ke dalam model ARIMA.

Tabel 6.

Estimasi dan Uji Signifikansi Parameter Model ARIMA (0,1,1)(0,1,1)¹² Jumlah Wisatawan Mancanegara dengan data outlier yang signifikan.

Parameter	Estimasi	p-value	Lag	Variabel	Keputusan
θ1	0,48621	<,0001	1	x1	Signifikan
θ12	0,85071	<,0001	12	x1	Signifikan
ω1	-21422	0,0016	0	LS22	Signifikan
ω2	27689	0,0002	0	LS83	Signifikan
ω3	16399	0,0258	0	AO110	Signifikan

Sumber : Data diolah (2104)

Berdasarkan pengujian residual model ARIMA (0,1,1)(0,1,1)¹² JumlahWisatawan Mancanegara dengan data outlier yang signifikan menunjukkan bahwa residual sudah white noise dengan nilai p-value yang lebih besar dari α = 0,05 . Sedangkan pengujian asumsi kenormalan

dengan uji Kolmogorov-Smirnov dengan taraf signifikansi 5 % memiliki nilai p-value lebih dari 0,05. Sehingga dapat disimpulkan bahwa residual sudah memenuhi asumsi berdistribusi normal, seperti terlihat pada Tabel 8.

Tabel 7.

Hasil Uji White Noise Residual Model ARIMA(0,1,1)(0,1,1)¹² Jumlah Wisatawan Mancanegara dengan data outlier yang signifikan

Lag	Chi-Sqrt	DF	p-value	Keputusan
6	1,37	4	0,8493	White Noise
12	5,62	10	0,8459	White Noise
18	12,98	16	0,6744	White Noise
24	15,56	22	0,8370	White Noise
30	24,56	28	0,6505	White Noise

Sumber : Data diolah (2104)

Tabel 8.

Hasil uji normalitas residual Model ARIMA (0,1,1)(0,1,1)¹² Jumlah Wisatawan Mancanegara dengan data outlier yang signifikan

Test                   D_hitung          p-value	Keputusan
Kolmogorov-Smirnov           0,065548          0,0994	Berdistribusi Normal

Sumber : Data diolah (2104)

Persamaan Model ARIMA (0,1,1)(0,1,1)¹² Jumlah Wisatawan Mancanegara dengan data outlier yang signifikan adalah sebagai berikut : X =-21422LS22 - 27689LS83-163999^0110

^t                                                         .....7

+(1-0,486215 - 0,8507LS¹²) at

Model Intervensi

Intervensi adalah suatu model yang digunakan saat kejadian-kejadian eksternal diluar perkiraan maupun kejadian-kejadian internal yang diperkirakan mempengaruhi variabel yang diramalkan.

180,000

160,000

140,000

120,000

100,000

80,000

60,000

40,000

20,000

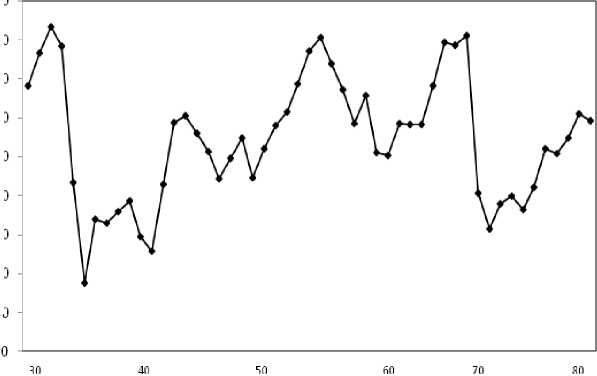
Gambar 5

Time Series Plot Kejadian Bom Bali 2002 dan Bom Bali 2005 pada t=34 dan t=70

Hasil identifikasi model intervensi dengan melihat plot ACF dan PACF dapat dilihat pada Gambar 6 dan Gambar 7.

Autocorrelations

Partial Autocorrelations

Lag -1

• 1|

• 2|

• 3|

• 4|

• 5|

• 6|

• 7|

• 8|

• 9|

10|

11|

12|

13|

14|

15|

16|

17|

9 8 7

6 5 4 3 2 1  0  1 2 3 4 5 6 7 8 9 1

********

*

.

.

.

**.

*

.

.

****

.

**

.

.

*

.

*

.

.

***.

Lag

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

-1 9 8 7 6 5 4 3 2 1  0  1 2 3 4 5 6 7 8 9 1

*****

****

*

.

*

.

*

.

.

.

***

*

.

**.

.

**.

.

***

*********

**

*

**

Gambar 6

Plot ACF Model Intervensi Jumlah Wisatawan Mancanegara

Pada Gambar 5 Secara umum dapat dilihat bahwa pengaruh terhadap kejadian intervensi yaitu kejadian bom bali 2002 pada saat t=34 dan bom bali 2005 pada saat t=70 tidak hanya terjadi pada saat kejadian saja, namun masih berpengaruh pada bulan-bulan berikutnya. Sehingga dengan proses iterasi pengaruh kejadian intervensi bom bali pada tahun 2002 signifikan sampai lag ke-3 dan untuk kejadian bom bali tahun 2005 signifikan sampai lag ke-2.

Gambar 7

Plot PACF Model Intervensi Jumlah Wisatawan Mancanegara

Proses pengolahan tidak hanya berhenti smapai disini ternyata asumsi belum sepenuhnya terpenuhi, dimana residualnya belum berdistribusi normal. Langkah selanjutnya mendeteksi adanya outlier yang menyebabkan residual belum berdistribusi normal. Hasil estimasi dan uji signifikansi parameter jumlah wisatawan mancanegara dengan data outliar yang signifikan seperti pada Tabel 9.

Tabel 9

Estimasi dan Uji Signifikansi Parameter Model Intervensi Jumlah Wisatawan Mancanegara dengan data outlier yang signifikan

Parameter	Estimasi	p-value	Lag	Variabel	Shift	Keputusan
θ1	0,35552	<,0001	1	y1	0	Signifikan
θ12	0,90553	<,0001	12	y1	0	Signifikan
ω1	-12966,3	0,0444	0	b1	3	Signifikan
ω2	17808,1	0,0171	0	b2	2	Signifikan
ω3	-15004,7	0,0159	0	LS22	0	Signifikan

Sumber : Data diolah (2104)

Tabel 10

Hasil Uji White Noise Residual Model Model Intervensi Jumlah Wisatawan Mancanegara dengan data outlier yang signifikan

Lag	Chi-Sqrt	DF	p-value	Keputusan
6	6,74	4	0,1505	White Noise White Noise White Noise White Noise
12	12,26	10	0,2679
18	14,73	16	0,5448
24	18,62	22	0,6686
30	24,30	28	0,6655

Berdasarkan pengujian residual model intervensi jumlah wisatawan mancanegara dengan data outlier yang signifikan menunjukkan bahwa residual sudah white noise dengan nilai p-value yang lebih besar dari α = 0,05. Sedangkan pengujian asumsi

kenormalan dengan uji Kolmogorov-Smirnov dengan taraf signifikansi 5 % memiliki nilai p-value lebih dari 0,05. Sehingga dapat disimpulkan bahwa residual sudah memenuhi asumsi berdistribusi normal, seperti terlihat pada Tabel 11.

Tabel 11

Hasil uji normalitas residual Model Model Intervensi Jumlah Wisatawan Mancanegara dengan data outlier yang signifikan

Test                  D_hitung          p-value	Keputusan
Kolmogorov-Smirnov          0,065548          0,0994	Berdistribusi Normal

Sumber : Data diolah (2104)

Pemilihan Model Terbaik

Persamaan model intervensi jumlah Wisatawan

Hasil analisis dari kedua model yaitu model

Mancanegara dengan data outlier yang signifikan

ARIMA dan model intervensi, model terbaik adalah sebagai berikut :

adalah model ARIMA berdasarkan data in-

y_t =-12966,3bl -17808,1b2 +15004,7LS22     sample maupun data out-sample dengan melihat

+ (1 _- 0,35552B - 0,90553B¹²)a_t           kriteria AIC, SBC maupun nilai RMSE memiliki

^{(8 )} nilai terkecil seperti terlihat pada Tabel 12 dan 13.

Tabel 12

Kriteria Pemilihan Model berdasarkan data in-sample

Model                       AIC	SBC
ARIMA                    3405,07 Intervensi                        3417,814	3420,288 3433,031

Sumber : Data diolah (2104)

Tabel 13

Kriteria Pemilihan Model berdasarkan data out-sample

Model           RMSE

ARIMA         3652,034

Intervensi           7872,974

Sumber : Data diolah (2104)

Ramalan Jumlah Wisatawan Mancanegara yang wisatawan mancanegara yang dating ke Bali pada

Datang ke Bali Tahun 2014                       Tahun 2014 seperti yang tercantum pada Tabel 14

Berdasarkan pemilihan model terbaik berikut.

sebelumnya, dapat dilakukan peramalan jumlah

Tabel 14

Hasil Ramalan Jumlah Wisatawan Mancanegara Yang Datang Ke Bali Tahun 2014 berdasarkan Model ARIMA

Bulan             Ramalan           Aktual         Bulan	Ramalan       Aktual
Januari               282377            278685           Juli Februari             271047            269367         Agustus Maret              279828           268418       September April              281587           277925        Oktober Mei              283617             -          Nopember Juni               304896               -           Desember	329544          - 326066          - 321443          - 302487          - 297365          - 311345          -

Dari tabel 14, hasil peramalan menggunakan Model ARIMA terhadap jumlah wisatawan mancanegara yang datang ke Bali pada Tahun 2014 tidak berbeda jauh hasilnya dengan jumlah aktual.

SIMPULAN DAN SARAN

Simpulan

Berdasarkan rumusan masalah dan pembahasan analisis yang telah dilakukan, dapat diambil kesimpulan dari hasil kedua model yaitu model Intervensi dan model ARIMA pada kasus jumlah kunjungan wisatawan mancanegara yang datang melalui Bandara Ngurah Rai sejak tahun 2000 sampai dengan April tahun 2014, bahwa metode peramalan yang terbaik adalah dengan model ARIMA. Hal ini dapat dilihat dari nilai AIC dan SBC terkecil berdasarkan data in-sample. Pemilihan model terbaik juga dapat didasarkan dari kesalahan out-sampel yang ditunjukkan nilai RMSE nya, dimana nilai RMSE model ARIMA lebih kecil dari model Intervensi. Dari hasil ramalan dengan Model ARIMA, jumlah wisatawan mancanegara yang datang ke Bali pada bulan Januari Tahun 2014 adalah 282377 orang, sedangkan data aktualnya sejumlah 278685 orang. Begitu juga hasil ramalan pada bulan Februari, Maret dan April 2014 yang tidak berbeda jauh dengan data aktual.

Saran

Untuk penelitian berikutnya, dapat disarankan bahwa untuk melakukan peramalan berdasarkan data

runut waktu (time series data), dapat menggunakan model ARIMA maupun model peramalan lain. Hal tersebut disarankan agar ada pebandingan ketepatan akan analisis time series dan sangat bermanfaat bagi penetapan strategi meningkatkan sektor pariwisata yang dapat menarik wisatawan untuk berkunjung ke Bali.

REFERENSI

Badan Pusat Statistik Provinsi Bali, 2000-2013 . Statistik Wisatawan Mancanegara ke Bali

Badan Pusat Statistik Provinsi Bali. BRS Pariwisata bulan Januari 2014

__________ BRS Pariwisata bulan Februari 2014 __________ BRS Pariwisata bulan Maret 2014 __________ BRS Pariwisata bulan April 2014

Box, G.E., Jenkins, G., & Reinsel, G.C. 1994. Time Series Analysis:Forecasting and Control (3rd ed. ). New Jersey.

Bowerman, B.L., & O’Connel, R.T. 1993. Forecasting and Time Series: An. Applied Approach. California: Duxbury Press.

Rukini. 2014. Model ARIMAX dan Deteksi GARCH untuk Peramalan Inflasi Kota Denpasar Tahun 2014. Jurnal Ekonomi Kuantitatif Terapan.Vol.

7. No. 2.pp 168-182

Wei, W. S. 2006. Time Analysis Univariate and Multivariate Methods, New York : Addison

Wesley Publishing Company, Inc.