MODEL BOX- JENKINS DALAM RANGKA PERAMALAN PRODUK DOMESTIK REGIONAL BRUTO PROVINSI BALI
on
92 Jurnal Buletin Studi Ekonomi, Vol. 19, No. 1, Februari 2014
MODEL BOX- JENKINS DALAM RANGKA PERAMALAN
PRODUK DOMESTIK REGIONAL BRUTO PROVINSI BALI
Made Suyana Utama1
I Gusti Putu Nata Wirawan2
(1)(2) Jurusan Ekonomi Pembangunan Fakultas Ekonomi dan Bisnis Universitas Udayana E-mail : suyanautama@gmail.com
Abstract : Box-Jenkins Models in the Framework to Forecast Bali Province Gross Domestic Product. Gross Domestic Product ( GDP ) is the most widely used indikator of development. In order to make development plan of an area with effective and responsible principal, it required a valid estimate of GDP. The presence of relatifly large gap between targets and achievements of the Bali Provincial economic growth during 2008-2012, and given the importance of GDP as an indikator of regional economic performance, it is necessary to do research on the application of Box-Jenkins models in order to forecast Bali Province GDP. This study aims to create a model of the Bali Provincial GDP estimates using data from the first quarter of GDP in 2000 to fourth quarter of GDP in 2012 with constant prices of 2000, which is sourced from BPS of Bali Province . The analysis technique is applied to the Box- Jenkins models or Autoregresive Integreted Moving Average (ARIMA).The results showed that by using the data of Bali Provincial GDP first quarter of 2000 to the fourth quarter of 2012, concluded that the best model to use as a forecast model is ARIMA (2,1,0).
Keywords : GDP , Autoregresive Integreted Moving Average
Abstrak : Model Box-Jenkins Dalam Rangka Peramalan Produk Domestik Regional Bruto Provinsi Bali. Produk Domestik Regional Bruto (PDRB) merupakan indikator pembangunan yang paling banyak digunakan. Dalam rangka membuat perencanaan pembangunan di daerah dengan prinsip efektif dan bertanggung jawab diperlukan perkiraan PDRB yang valid. Adanya selisih yang relatif cukup besar antara target dan capaian pertumbuhan ekonomi Provinsi Bali selama tahun 2008 - 2012, dan mengingat pentingnya PDRB sebagai indikator kinerja perekonomian daerah, maka dipandang perlu melakukan penelitian mengenai penerapan model Box-Jenkins dalam peramalan PDRB Provinsi Bali. Penelitian ini bertujuan untuk membuat model estimasi PDRB Provinsi Bali dengan menngunakan data PDRB dari triwulan I tahun 2000 sampai dengan triwulan IV tahun 2012 dengan harga konstan tahun 2000, yang bersumber dari Badan Pusat Statistik (BPS) Provinsi Bali. Teknik analisis yang diterapkan adalah model Box-Jenkins atau Autoregresive Integreted Moving Average (ARIMA). Hasil penelitian menunjukkan bahwa dengan menggunakan data PDRB Provinsi Bali triwulan I tahun 2000 sampai dengan triwulan IV tahun 2012, disimpulkan bahwa model peramalan yang terbaik adalah dengan ARIMA(2,1,0).
Kata kunci: PDRB, Autoregresive Integreted Moving Average
PENDAHULUAN
Latar Belakang
Dengan dilaksanakannya otonomi daerah di Indonesia, yaitu dengan diberlakukannya UU No. 22 tahun 1999 yang direvisi menjadi UU No. 32 tahun 2004 paradigma pembangunan di daerah telah berubah, terkait perubahan sistem dan mekanisme perencanaan pembangunan daerah di Indonesia. Implikasi penting dari pelaksanaan otonomi daerah, kewenangan yang luas dan nyata yang bertanggung jawab (accountable) telah diberikan kepada daerah secara proporsional. Hal ini menuntut tiap daerah untuk meningkatkan kinerja perekonomian daerah.
Variabel yang dominan digunakan untuk mengetahui kinerja perekonomin pada suatu wilayah adalah tingkat pertumbuhan ekonomi dari waktu ke
waktu (Gregory dan Stuart, 1992). Pada tingkat nasional pertumbuhan ekonomi dihitung yang digunakan adalah nilai Produk Domestik Bruto (PDB) atas harga konstan (Rahardja dan Manurung, 2001). PDB didefinisikan sebagai nilai barang dan jasa yang dihasilkan pada suatu wilayah perekonomian selama jangka waktu tertentu (Abel, Andrew B. and Ben S. Bernake, 2001). Suatu perekonomian dikatakan mengalami pertumbuhan jika jumlah produksi barang dan jasa yang dihasilkan meningkat. Tingkat pertumbuhan ekonomi yang tinggi dan berkesinambungan merupakan kondisi yang diinginkan setiap negara dan daerah. Angka pertumbuhan yang tinggi menunjukkan adanya peningkatan ketersediaan lapangan kerja dan pendapatan yang pada akhirnya diharapkan akan meningkatkan kesejahteraan dan kemakmuran masyarakat secara keseluruhan.
Sebagai indikator kinerja perekonomian, PDB maupun PDRB sering diperkirakan tidak tepat atau meleset. Pihak eksekutif cenderung memasang target yang rendah terhadap perencanaan PDRB pada periode ke depan, sedangkan pihak legislatif menuntut agar eksekutif angka lebih tinggi, agar pemerintah termotivasi bekerja lebih giat untuk meningkatkan kinerja perekonomian. Gambar 1 memberikan informasi bahwa selisih target dan capaian pertumbuhan ekonomi Provinsi Bali tahun 2008 – 2012, relatif cukup tinggi, yaitu dengan rata-rata -0,54 persen per tahun.

Sumber : BPS Provinsi Bali, 2013
Gambar 1
Target dan Capaian Pertumbuhan Ekonomi
Provinsi Bali, Tahun 2008 - 2012
Dengan adanya selisih yang relatif cukup besar antara target dan capaian pertumbuhan ekonomi, dan mengingat pentingnya PDRB sebagai indikator kinerja perekonomian daerah, maka dipandang perlu melakukan penelitian mengenai penerapan model Box-Jenkins dalam peramalan PDRB Provinsi Bali. Box dan Jenkins mempopulerkan metode yang terdiri dari 3 tahap dalam memilih model yang cocok untuk melakukan estimasi dan peramalan data runtut waktu univariat, yaitu identifikasi model, estimasi parameter, dan peramalan (Enders, 2008). Dengan kata lain metode Box-Jenkins adalah teknik melacak sebaran dan menganalisis data runtut waktu apakah mengikuti pola Autoregresive (AR), atau mengikuti pola Moving Average (MA), atau mengikuti pola Autoregresive Moving Average (ARMA) atau mengikuti pola Autoregresive Integreted Moving Average (ARIMA) dan selanjutkan meramalkannya. (Gujarati, 2009). Dibandingkan dengan metode trend yang menggunakan Ordinary Least Square (OLS) metode Box-Jenkins lebih akurat karena dikoreksi oleh residualnya.
Penelitian ini bertujuan untuk membuat model estimasi PDRB Provinsi Bali dari triwulan I tahun 2000 sampai dengan triwulan IV tahun 2012, dengan model Box-Jenkins, dan membuat ramalan PDRB Provinsi Bali triwulan I tahun 2013 sampai dengan triwulan IV tahun 2014.
KAJIAN PUSTAKA
Produk Domestik Regional Bruto (PDRB)
PDRB merupakan jumlah nilai tambah yang dihasilkan oleh seluruh unit usaha (sektor – sektor ekonomi) dalam suatu wilayah dan periode waktu tertentu. Oleh karena itu, pertumbuhan ekonomi di suatu wilayah adalah sama dengan pertumbuhan PDRB di wilayah tersebut. Apabila diibaratkan kue, PDRB adalah besarnya kue tersebut. pertumbuhan ekonomi sama dengan membesarnya kue tersebut yang pengukurannya merupakan persentase pertambahan PDRB pada periode tertentu terhadap PDRB periode sebelumnya. Hasil penghitungan PDRB biasa dikenal sebagai PDRB menurut lapangan usaha (sektoral) maupun PDRB menurut pengeluaran/penggunaan (BPS Provinsi Bali, 2013).
Pendekatan Perhitungan PDRB
Pendekatan perhitungan PDRB sama dengan perhitungan PDB dan pendapatan nasional, yaitu melalui 3 pendekatan (approach), yaitu: 1) Pendekatan produksi (production approach), 2) Pendekatan pengeluaran (expenditure approach) dan 3) Pendekatan pendapatan (income approach).
Pendekatan produksi (production approach)
Pendekatan ini adalah dengan cara menjumlahkan nilai tambah (value added) barang-barang dan jasa-jasa yang diproduksi oleh berbagai sektor ekonomi (lapangan usaha) di dalam negara tersebut. Tujuan dari pendekatan ini adalah untuk mengetahui sumbangan dari berbagai sektor ekonomi terhadap ekonomi nasional, dan juga sebagai salah satu cara untuk meninghindarkan perhitungan yang ganda (double accounting).
Pendekatan pengeluaran (expenditure approach)
Pendekatan ini dilakukan dengan menjumlahkan nilai pengeluaran barang-barang dan jasa-jasa oleh berbagai sektor di negara tersebut. Sesuai dengan aliran pendapatan pada suatu perekonomian seperti Gambar 2, maka pengeluaran ini dibedakan menjadi 4 komponen, yaitu : pengeluaran untuk konsumsi rumah tangga, pengeluaran pemerintah, pembentukan modal pada sektor swasta dan ekspor neto (ekspor dikurangi impor).
Pengeluaran konsumsi rumah tangga adalah nilai barang dan jasa yang dibeli oleh rumah tangga untuk memenuhi kebutuhannya. Pengeluaran ini terdiri dari pengeluaran untuk bahan makanan dan bukan bahan makanan, seperti untuk pakaian, pengangkutan, biaya
pendidikan sewa rumah dan membeli kendaraan. Tetapi pengeluaran untuk masa depan, seperti biaya pembelian rumah, asuransi, kiriman untuk orang tua atau untuk anak yang sedang sekolah tidak digolongkan ke dalam pengeluaran konsumsi, tetapi investasi.

Gambar 2
Aliran Melingkar Pendapatan Dan Pengeluaran
Pengeluaran Lembaga Swasta Nirlaba/Non Profit. Penilaian terhadap barang dan jasa layanan (output) disetarakan dengan biaya yang dikeluarkan (input). Biaya yang dikeluarkan oleh lembaga terdiri dari nilai penggunaan barang dan konsumsi) antara dan nilai penggunaan faktor produksi, akan diperoleh penghitungan pengeluaran lembaga swasta yang tidak mencari untung.
Pengeluaran pemerintah terdiri dari pengeluaran pemerintah dalam rangka menjalankan fungsinya melayani masyarakat dalam menyediakan jasa publik, misalnya fasilitas pendidikan, kesehatan, keamanan/ pertahanan dan fasilitas pemerintahan lainnya yang disebut konsumsi pemerintah, serta investasi pemerintah yang meliputi semua pengeluaran untuk membangun prasarana, seperti jalan, sekolah, rumah sakit, irigasi dan lain sejenisnya. Sedangkan pengeluaran untuk beasiswa, bantuan pengungsi dan subsidi-subsidi tidak digolongkan pengeluaran pemerintah terhadap produk nasional, karena tidak merupakan pembelian barang dan jasa.
Pembentukan Modal Tetap Bruto (PMTB) yang sering disebut investasi, yang pada dasarnya merupakan pengeluaran untuk barang modal yang bertujuan untuk menaikkan produksi barang dan jasa dikemudian hari. Investasi ini dapat berupa pembelian peralatan produksi, perubahan atas persediaan nilai inventori pada akhir tahun dan pembelian rumah tinggal.
Perubahan Stok/Inventori. Data mengenai perubahan stok/inventori dalam komponen penggunaan PDRB ini masih merupakan hasil penjumlahan nilai tambah bruto sektoral minus komponen akhir lainnya seperti pengeluaran konsumsi rumahtangga, pengeluaran konsumsi pemerintah, pembentukan modal tetap domestik bruto dan ekspor neto. Jadi di dalam perubahan stok tersebut, masih terkandung selisih statistik atau diskrepansi statistic (statistical discrepancy) yang terdapat pada sektor atau komponen lainnya.
Ekspor neto, merupakan nilai ekspor suatu negara pada tahun tertentu yang dikurangi dengan nilai impor pada piode yang sama. Ekspor merupakan penjualan barang dan jasa yang diproduksi di dalam negeri, sehingga nilainya harus dihitung ke dalam pendapatan nasional.
METODE PENELITIAN
Data Penelitian
Penelitian ini dilaksanakan di Provinsi Bali dengan memanfaatkan data yang dikumpulkan dan diolah atas kerjasama Kantor Bank Indonesia Denpasar dengan Badan Statistik Provinsi Bali, dalam bentuk Kajian Ekonomi Regional (KER) Provinsi Bali Triwulanan, dari triwulan I tahun 1992 sampai dengan triwulan IV tahun 2012.
Teknik Analisis Data
Untuk meramalkan PDRB Bali dalam kurun waktu yang cukup lama, yaitu dari dari triwulan I tahun 2000 sampai dengan triwulan IV tahun 2012. Data bersumber dari Badan Pusat Statistik Provinsi Bali, yang selanjutnya dianalisis dengan menggunakan model Box-Jenkins.
Box dan Jenkins mempopulerkan metode peramalan data univariat runtut waktu yang terdiri dari 3 tahap dalam memilih model yang cocok untuk melakukan estimasi dan peramalan. Peramalan (forecasting) dengan menggunakan data runtun waktu (time series) secara sederhana sering dilakukan dengan analisis trend. Namun agar hasil peramalan lebih akurat, terutama untuk data runtun waktu yang cukup panjang, maka data runtun waktu dapat dianalisis dengan mempertimbangkan berbagai perilaku data melalui berbagai model antara lain model autoregressive (AR), moving average (MA) dan autoregressive moving average (ARIMA) (Ghozali, 2007), yang dijelaskan sebagai berikut.
Autoregresive (AR)
Misalkan Yt adalah PDRB pada waktu t. Jika kita membuat model Yt sebagai:
(Yt - δ) = αι (Yt-1 - δ) + μt.........................(1)
Dimana δ adalah mean dari Y dan ut error term yang tidak berkorelasi dengan mean = nol dan variance (σ2) konstan ( white noise), maka kita dapat mengatakan Yt mengikuti pola stochastic first order autoregressive atau AR(1). Disini nilai Y pada waktu t tergantung dari nilai periode waktu sebelumnya ditambah dengan error term. Dengan kata lain nilai peramalan Y pada waktu t merupakan proporsi (=α1) dari nilai Y pada waktu (t-1 ) ditambah random shock atau residual pada waktu t. Hal ini dapat diperlihatkan model: (Yt - δ ) = α1 (Yt,ι-δ) + α2 (Yt,2 - δ) + μt............(2)
Model dengan nilai Y pada waktu t tergantung dari nilai Y pada waktu dua periode masa lalu disebut juga second order autoregressive process atau AR(2). Dalam hal ini nilai Y dinyatakan disekitar nilai mean δ. Secara umum model autoregressive dapat dituliskan: (Yt - δ )=αι (Yt, - δ )+«2 (Yt, - δ ) ... αp Y - δ )+μt..............(3)
Dimana Yt adalah pola autoregresif order ke-p (pth-order autoregressive process atau AR(p).
Moving Average (MA)
Selain melalui proses model autoregresif (AR), memprediksi nilai Y juga dapat dilakukan melalui proses
model moving average (MA). Model ini memanfaatkan u yang merupakan white noise stochastic error. Contoh model MA ditunjukkan sebagai berikut:
Yt = u + βo ut + βι ut -i..............................(4)
Dalam hal ini u adalah konstanta, dan Y pada waktu t sama dengan konstanta ditambah moving average dari error sekarang dan error masa lalu. Model seperti ini disebut Y mengikuti first order moving average process atau MA(1), dan untuk second order moving average process atau MA(2) ditunjukkan dengan model:
Yt = u + βo ut + β1 ut -1 + β2 ut -2........................(5)
Secara umum model moving average (MA) pada order ke-p ditunjukkan dengan model:
Yt = u + βo ut + β1 ut -1 + β2 ut-2......βp ut -p........................(6)
Pola Autoregresive dan Moving Average (ARMA)
Memprediksi nilai Y juga dapat dilakukan melalui proses Autoregresive dan Moving Average (ARMA). Hal ini dimungkinkan karena Y juga memiliki karakteristik AR dan MA. Untuk model ARMA(1,1), maka proses peramalan atau prediksi terhadap Yt dapat dinotasikan sebagai berikut:
Y,=θ+α Ym+βout+β1 uM............................(7)
Nilai θ merupakan konstanta, dan model 2.7 merupakan model ARMA dengan satu autoregressive dan satu moving average. Peramalan Yt secara umum dapat dilakukan dengan p autoregressive dan q moving average yang diringkas menjadi ARMA(p,q).
Pola Autoregresive Integreting Moving Average (ARIMA)
Seperti telah dijelaskan sebelumnya, bahwa model dengan menggunakan data runtun waktu (time series) diasumsikan dalam kondisi stationer, yang mana mean dan variance adalah konstan, serta covariance adalah time-invariant. Namun harus dimaklumi bahwa banyak data ekonomi runtun waktu tidak bersifat stationer atau integrated. Demikian juga telah dipahami bahwa jika data time series intergrated pada order 1 atau 1(1), maka nilai difference pertama atau 1(0) adalah stationer. Dengan cara yang sama jika data runtun waktu adalah 1(2), maka nilai difference kedua adalah 1(0). Secara umum dapat dikatakan bahwa jika data runtun waktu I(d), setelah di difference sebanyak d kali akan didapatkan 1(0) seri.
Oleh karena itu jika data runtun waktu didifference sebanyak d kali untuk mendapatkan data stationer kemudian diaplikasikan pada model ARMA(p.q), maka model ini disebut Autoregresive Integrated Moving Average atau ARIMA (p,d,q). Dalam hal ini p adalah jumlah autoregressive, d jumlah (berapa kali) data harus didifference agar data menjadi stationer, dan q adalah jumlah moving average. Dengan demikian ARIMA(2,1,2) berarti data runtun waktu yang didifference sekali (d= 1), memiliki dua autoregressive dan dua moving average. ARIMA(p,d=0,q) merupakan ARMA(p,q), ARIMA(p,0,0) sama dengan AR(p) dan ARIMA(0,0,q) sama dengan MA(q).
Dimana n = sample size dan m = panjang lag. Q statistik sering digunakan untuk menguji apakah data time series dalam kondisi white noise atau tidak. Dengan menggunakan sample besar, distribusi Q statistik mendekati distribusi chi-square dengan degree of freedom sebesar m. Varians dari Box-Pierce Q statistik diperbaiki oleh Ljung-Box yang dikenal dengan (LB) statistic yang didefinsikan:
m
LB = n (n + 2) ∑
k=1
2
Pk
^ n - k
2m
...……...…..(9)
Tahapan Motode Box-Jenkins (BJ)
Suatu data runtun waktu perlu dilacak apakah data ini mengikuti pola AR (jika ya, berapa nilai p) atau mengikuti pola MA (dan jika ya, harus diketahui berapa nilai q) atau mengikuti pola ARMA (jika ya, harus diketahui berapa nilai p dan q), atau mengikuti pola ARIMA (jika ya, harus diketahui berapa nilai p, d, dan q. Oleh karena itu, untuk menjawab pertanyaan ini dapat dilakukan dengan metode Box-Jenkins. Metode ini terdiri dari empat langkah, yaitu:
Identifikasi: yaitu menentukan nilai yang tepat p, d, dan q dengan cara mengamati correlogram dan partial correlogram. Identifikasi ARIMA untuk PDRB dapat dilakukan dengan melihat correlogram dan partial correlogram data yang stationer. Untuk melihat kestasioneran data yang dapat dilakukan dengan melihat nilai autocorrelation (AC). Untuk pola yang white noise, maka nilai autocorrelation pada berbagai lag akan mempunyai nilai yang mendekati nol. Pengujian dilakukan dengan joint hypothesis bahwa semua koefisien autokorelasi sampai lag tertentu secara simultan sama dengan nol. Hal ini dapat dilakukan dengan menggunakan Q statistik yang dikembangkan oleh Box dan Pierce yang didefinisikan sebagai berikut:
Nilai Q dan LB statistic pada sample besar mengikuti distribusi Chi-square dengan derajat bebas m, tetapi LB statistic lebih baik dari pada Q statistic untuk sample kecil.
Untuk mendeteksi distribusi suatu data yang stasioner ataukah tidak, dapat juga dilihat dari grafik autocorrelation function (ACF) apakah melewati batas interval konfidensi. Konsep terkini yang banyak dipakai untuk menguji kestasioneran data runtun waktu adalah uji akar unit (unit root test) atau dikenal juga dengan uji Augmented Dickey Fuller (ADF). Seperti telah dijelaskan sebelumnya, bahwa data bersifat stasioner adalah data dengan perilaku data yang memiliki varians yang tidak terlalu besar dan mempunyai kecenderungan untuk mendekati nilai rata-ratanya. Dalam hal ini persamaan yang
digunakan adalah:
(Yt - Yt-1) = ρ Yt-1 -Yt-1 + μt ................(10)
= (p - 1) Yt-ι + μt
Atau dapat ditulis:
∆Yt = pYt—1 + μt...............................(11)
Dimana: δ = (p - 1) dan ∆ adalahfirst diference
m
Q = n ∑ Pk
k=1
…………………………….(8)
Analisis dilakukan dengan membuat regresi antara ∆Yt frst d,jferenι) dan Yt 1 sehingga akan didapat koefisien regresinya, yaitu δ. Regresi metode yang sama secara parsial juga akan dilakukan terhadap semua variabel independen yang digunakan. Jika tidak signifikan berarti, maka data tidak stationer.
Selanjutnya untuk mendeteksi apakah pola AR atau MA atau ARIMA dapat digunakan pedoman Tabel 1.
Tabel 1.
Jenis Model Peramalan dengan Melihat Pola AC dan PAC
|
Jenis Model |
Pola AC Pola PAC |
|
AR(p) MA(q) ARMA(p,q) |
Menurun secara exponential Menurun drastis pada lag tertentu Menurun drastis pada lag tertentu Menurun secara exponential Menurun secara exponential Menurun secara exponential |
Estimasi Model Tentatif: setelah menentukan nilai p dan q yang sesuai, langkah berikutnya adalah mengestimasi parameter autoregressive dan moving average yang dimasukkan dalam model.
Diagnostic Checking: setelah memilih model ARIMA dan setelah mengestimasi parameter, langkah selanjutnya adalah menguji apakah model ARIMA yang telah dipilih fit (cocok atau sesuai) karena mungkin ada model ARIMA lainnya yang lebih fit dengan data yang ada. Jadi Model ARIMA Box-Jenkins lebih condong pada seni daripada science. Keahlian diperlukan dalam memilih model ARIMA tepat. Salah satu cara menguji model yang terpilih adalah dengan melihat nilai residual yang diestimasi dari model adalah white noise. Jika jawabannya ya, maka kita menerima model yang fit, tetapi jika jawaban tidak, harus memulai lagi dari awal. Sehingga metode BJ merupakan proses iterasi.
Memilih Model ARIMA. Pada suatu saat peneliti dihadapkan pada dilema, misalnya dua model ARIMA yang dibuat sama baiknya berdasarkan metode sebelumnya. Untuk memilih model yang terbaik dari beberapa model yang baik, perkenalkan Akaike Information Criterion (AIC) yang dikembangkan oleh Prof. Harotugu Akaike, dan juga Bayesian Information Criteria (BIC) yang dikembangkan oleh Schwarz. Oleh karena dikembangkan oleh Schwarz, maka model
BIC juga disebut model SIC. Semakin kecil nilai AIC, BIC atau SIC semakin baik model yang dibuat.
Peramalan: salah satu alasan penting popularitas dari model ARIMA adalah keberhasilannya didalam peramalan. Pada banyak kasus peramalan yang didapat dari metode ARIMA lebih reliabel atau handal daripada peramalan yang didapat dari mode tradisional, khususnya untuk peramalan jangka pendek.
HASIL DAN PEMBAHASAN
PDRB Triwulanan Provinsi Bali
PDRB Provinsi Bali dengan harga konstan tahun 2000 per triwulan selama triwulan ke-1 tahun 2000, sampai dengan triwulan ke-4 tahun 2012, cukup berfluktuasi seperti yang disajikan pada Tabel 2. Hal ini tampak jelas bahwa secara triwulanan selama tahun 2000 – 2012 PDRB Bali ada yang mengalami kontraksi atau pertumbuhan yang negatif. Namun berbeda dengan PDRB tahunan selama periode yang sama tidak mengalami pertumbuhan yang negatif. Hal ini disebabkan karena data triwulanan cukup dipengaruhi oleh faktor musiman, seperti kunjungan wisatawan, cuaca, dan juga realisasi investasi serta anggaran pembangunan dari pemerintah
Tabel 2
Produk Domestik Regional Bruto Provinsi Bali Menurut Harga Konstan Tahun 2000, dari Triwulan I Tahun 2000 sampai dengan Triwulan IV Tahun 2012
|
Tahun, Triwulan |
PDRB (Rp milyar) |
Pertumbuhan (%) |
Tahun, Triwulan |
PDRB (Rp milyar) |
Pertumbuhan (%) |
Tahun, Triwulan |
PDRB (Rp milyar) |
Pertumbuhan (%) |
|
2000.1 |
4.184 |
2004.3 |
5.066 |
3,05 |
2009.1 |
6.440 |
0,16 | |
|
2000.2 |
4.253 |
1,64 |
2004.4 |
5.143 |
1,52 |
2009.2 |
6.510 |
1,09 |
|
2000.3 |
4.382 |
3,05 |
2005.1 |
5.302 |
3,09 |
2009.3 |
6.630 |
1,84 |
|
2000.4 |
4.449 |
1,52 |
2005.2 |
5.290 |
-0,23 |
2009.4 |
6.660 |
0,45 |
|
2001.1 |
4.332 |
-2,62 |
2005.3 |
5.326 |
0,68 |
2010.1 |
6.730 |
1,05 |
|
2001.2 |
4.403 |
1,64 |
2005.4 |
5.135 |
-3,58 |
2010.2 |
6.880 |
2,23 |
|
2001.3 |
4.538 |
3,05 |
2006.1 |
4.928 |
-4,03 |
2010.3 |
7.060 |
2,62 |
|
2001.4 |
4.606 |
1,52 |
2006.2 |
5.250 |
6,53 |
2010.4 |
7.390 |
4,67 |
|
2002.1 |
4.464 |
-3,09 |
2006.3 |
5.792 |
10,32 |
2011.1 |
7.450 |
0,81 |
|
2002.2 |
4.537 |
1,64 |
2006.4 |
6.189 |
6,86 |
2011.2 |
7.610 |
2,15 |
|
2002.3 |
4.676 |
3,05 |
2007.1 |
5.960 |
-3,70 |
2011.3 |
7.790 |
2,37 |
|
2002.4 |
4.747 |
1,52 |
2007.2 |
5.850 |
-1,85 |
2011.4 |
7.900 |
1,41 |
|
2003.1 |
4.623 |
-2,59 |
2007.3 |
5.850 |
0,00 |
2012.1 |
7.900 |
0,00 |
|
2003.2 |
4.699 |
1,64 |
2007.4 |
5.820 |
-0,51 |
2012.2 |
8.120 |
2,78 |
|
2003.3 |
4.842 |
3,05 |
2008.1 |
5.980 |
2,75 |
2012.3 |
8.320 |
2,46 |
|
2003.4 |
4.916 |
1,52 |
2008.2 |
6.140 |
2,68 |
2012.4 |
8.460 |
1,68 |
|
2004.1 |
4.837 |
-1,60 |
2008.3 |
6.350 |
3,42 | |||
|
2004.2 |
4.917 |
1,64 |
2008.4 |
6.430 |
1,26 |
Sumber: BPS Provinsi Bali, 2013
Selama periode 2000 – 2012 pertumbuhan PDRB triwulanan Provinsi Bali paling tinggi sebesar 10,32 persen, sedangkan paling rendah negatif 4,03 persen, dengan rata-rata 1,42 persen. Pertumbuhan negatif atau kontraksi terjadi pada triwulan ke-1 tahun 2006, yaitu setelah terjadi tragedi Bom Kuta II tahun 2005. Setelah itu, pada triwulan ke-3 tahun 2006 ekonomi Bali tumbuh drastis dengan pertumbuhan 10,32 persen.
Uji Kestasioneran Data
Persyaratan data yang akan dianalisis dengan model Box-Jenkins adalah harus stasioner. Data bersifat stasioner adalah data dengan perilaku data yang memiliki varians yang tidak terlalu besar dan mempunyai kecenderungan untuk mendekati nilai rata-ratanya. Beberapa cara menguji kestasioneran data diantaranya adalah dengan: 1) metode grafik, 2) correlogram, dan 3) dengan metode akar unit (unit root test).
Metode Grafik
Berdasarkan Gambar 3 dapat diketahui bahwa PDRB Bali mempunyai trend yang meningkat. Sehingga dapat disimpulkan bahwa data runtun waktu PDRB Bali tidak stasioner. Kesimpulan ini rupanya bersifat subyektif, sehingga dapat dilakukan metode lainnya.
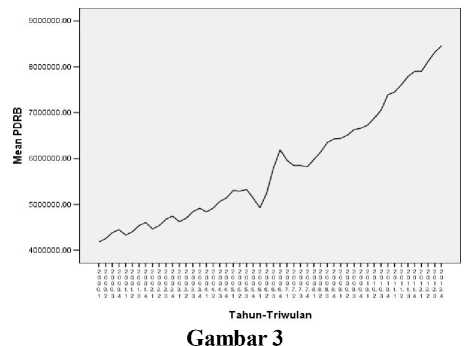
Perkembangan PDRB Bali Triwulan I. 2000 – Triwulan IV 2012
Correlogram dan Autocorrelation Function (ACF)
Untuk melihat kestasioneran data runtun waktu dapat dilakukan dengan melihat nilai autocorrelation (AC). Untuk pola yang white noise, maka nilai autocorrelation pada berbagai lag akan mempunyai nilai yang mendekati nol. Pengujian dilakukan dengan joint hypothesis bahwa semua koefisien autokorelasi sampai lag tertentu secara simultan sama dengan nol. Hal ini dapat dilakukan dengan menggunakan Q statistik yang dikembangkan oleh Box dan Pierce yang didefinisikan sebagai berikut:
m
Q = n ∑ Pk2 .....................................(12)
k=1
Dimana n = sample size dan m = panjang lag. Q statistik sering digunakan untuk menguji apakah data time series dalam kondisi white noise atau tidak. Dengan menggunakan sample besar, distribusi Q statistik mendekati distribusi chi-square dengan degree of freedom sebesar m. Varians dari Box-Pierce Q statistik diperbaiki oleh Ljung-Box yang dikenal dengan (LB) statistic yang didefinsikan:
m
LB = n (n + 2)∑
k=1
2 p-y n - k
∞χ
√
2m
………………..(13)
Nilai Q dan LB statistic pada sampel besar mengikuti distribusi Chi-square dengan derajat bebas m, tetapi LB statistic lebih baik dari pada Q statistic untuk sampel kecil.
Berdasarkan hasil olahan data dengan SPSS terlihat bahwa Correlogram untuk autocorrelation function (AC) mengalami penurunan secara lambat sampai lag 16 (default) dan secara individu signifikan secara statistik berbeda dari nol. Kedua, partial autocorrelation function (PAC) turun secara dramatis dan semua PAC. Keadaan seperti ini memperlihatkan bahwa data time series PDRB tidak stationer.
Uji Akar Unit (Unit Roots Test)
Konsep terkini yang banyak dipakai untuk menguji kestasioneran data runtun waktu adalah uji akar unit (unit root test) atau dikenal juga dengan uji Augmented Dickey Fuller (ADF). Seperti telah dijelaskan sebelumnya, bahwa sata bersifat stasioner adalah data dengan perilaku data yang memiliki varians yang tidak terlalu besar dan mempunyai kecenderungan untuk mendekati nilai rata-ratanya. Dalam hal ini persamaan yang digunakan adalah:
(Yt - Yt-1) = r Yt-1- Yt-1 + mt ………………..(14) = (r – 1) Yt-1 + mt
Atau dapat ditulis:
D Yt = d Yt-1 + mt………..........…...... (15)
D Yt = b1+ dYt-1 + mt……………….....(16)
D Yt = b1+ b2Yt + dYt-1 + mt…………..(17)
Dimana: d = (r – 1) dan D adalah first difference Dengan hipotesis sebagai berikut:
h : r = 0 artinya terjadi unit root (data tidak stationer) h : r ¹ 0 artinya tidak terjadi unit root (data stationer)
Analisis dilakukan dengan membuat regresi antara DYt (first different) dan Yt-1 sehingga akan didapat koefisien regresinya, yaitu ä. Regresi metode yang sama secara parsial juga akan dilakukan terhadap semua variabel independen yang digunakan. Jika tidak signifikan berarti, maka data tidak stationer.
|
Tabel 3 | ||||||
|
Nilai Autocorrelation (AC) dan Partial Autocorrelation (PAC) PDRB Bali Triwulanan, Tahun 2000 – 2012 | ||||||
|
Lag |
AC |
Std.Error PAC |
Std.Error |
Box-Ljung Statistic | ||
|
Value |
Df |
Sig.(b) | ||||
|
1 |
0,929 |
0,135 0,929 |
0,139 |
47,523 |
1 |
0,000 |
|
2 |
0,856 |
0,133 -0,054 |
0,139 |
88,648 |
2 |
0,000 |
|
3 |
0,792 |
0,132 0,030 |
0,139 |
124,576 |
3 |
0,000 |
|
4 |
0,738 |
0,131 0,033 |
0,139 |
156,403 |
4 |
0,000 |
|
5 |
0,678 |
0,129 -0,072 |
0,139 |
183,842 |
5 |
0,000 |
|
6 |
0,619 |
0,128 -0,019 |
0,139 |
207,206 |
6 |
0,000 |
|
7 |
0,564 |
0,127 -0,003 |
0,139 |
227,075 |
7 |
0,000 |
|
8 |
0,509 |
0,125 -0,046 |
0,139 |
243,622 |
8 |
0,000 |
|
9 |
0,445 |
0,124 -0,095 |
0,139 |
256,571 |
9 |
0,000 |
|
10 |
0,391 |
0,122 0,029 |
0,139 |
266,767 |
10 |
0,000 |
|
11 |
0,344 |
0,121 0,012 |
0,139 |
274,893 |
11 |
0,000 |
|
12 |
0,302 |
0,119 -0,009 |
0,139 |
281,307 |
12 |
0,000 |
|
13 |
0,255 |
0,118 -0,054 |
0,139 |
285,982 |
13 |
0,000 |
|
14 |
0,207 |
0,116 -0,033 |
0,139 |
289,159 |
14 |
0,000 |
|
15 |
0,166 |
0,115 0,003 |
0,139 |
291,262 |
15 |
0,000 |
|
16 |
0,126 |
0,113 -0,033 |
0,139 |
292,509 |
16 |
0,000 |
Sumber: Data Penelitian diolah
Berdasarkan data PDRB Bali dapat dianalisis kestasioneran data dengan menggunakan uji akar unit (Augmented Dickey-Fuller Unit Root Test) yang hasilnya disajikan pada Tabel 4.
Pengujian unit root adalah dengan melihat signifikansi dari koefisien Augmented Dickey-Fuller (ADF) dari PDRB_1. Nilai t hitung (ζ = tau) sebesar -0,802 yang berada pada daerah penerimaan hipotesis dengan probabilitas dari penerimaan Ho sebesar 0,426. Dengan demikian dapat disimpulkan bahwa data PDRB Bali tidak stasioner.
Merubah Data Runtun Waktu Non-Stasioner menjadi Stasioner
Metode Box-Jenkins menghendaki agar data yang dianalisis harus stationer, maka untuk itu data PDRB dibuat stationer. Data yang tidak stasioner dapat ditransformasi menjadi data stasioner agar regresi yang dihasilkan tidak semu (sporious). Caranya
adalah dengan melakukan proses deferensiasi, yaitu dengan mengurangkan PDRDt dengan PDRBt-1 (first difference).
Dt = ΔPDRBt = (PDRBt - PDRBt-1)......(4.7)
Grafik hasil olahan data PDRB Bali setelah didiferensi satu kali (d=1) nampak pada Gambar 4. Dari Gambar 4 dapat dilihat bahwa bahwa data PDRB Bali telah menjadi stasioner, yaitu dengan rata-rata dan varians nol, serta grafiknya tidak menunjukkan trend meningkat.
Dengan menggunakan unit root yang hasilnya disajikan pada Tabel 4 juga dapat diketahui bahwa signifikansi dari koefisien D1PDRB adalah sebesar 0,000 dengan nilai t hitung (ζ = tau) sebesar -6,418 yang berada di luar nilai t kritis pada tingkat signifikansi kurang dari 1 persen. Dengan demikian dapat disimpulkan bahwa data PDRB Bali stasioner pada diferensi satu.
Tabel 4.
Hasil Augmented Dickey-Fuller Unit Root Test Terhadap PDRB
|
Unstandardized Coefficients |
Standardized Coefficients Beta |
t |
Sig. | ||
|
B |
Std. Error | ||||
|
(Constant) |
-21554,198 |
102651,899 |
-0,210 |
0,835 | |
|
PDRB_1 |
0,014 |
0,018 |
0,116 |
0,802 |
0,426 |
|
D1PDRB_1 |
0,271 |
0,145 |
0,271 |
1,868 |
0,068 |
|
Dependent Variable: D1PDRB | |||||
Sumber: Data Penelitian diolah

Gambar 4
Perkembangan PDRB Bali Triwulan I. 2000 – Triwulan IV 2012 (Setelah Dideferensi 1)
Tabel 5.
Hasil Augmented Dickey-Fuller Unit Root Test terhadap PDRB (Setelah Dideferensi 1)
|
Unstandardized Coefficients |
Standardized Coefficients Beta |
t |
Sig. | ||
|
B |
Std. Error | ||||
|
(Constant) |
82323,824 |
22349,142 |
3,684 |
0,001 | |
|
PDRB_1 |
-1,004 |
0,156 |
-0,853 |
-6,418 |
0,000 |
|
D1PDRB_1 |
0,446 |
0,133 |
0,446 |
3,355 |
0,002 |
Dependent Variable: D1PDRB
Sumber: Data Penelitian diolah
Tabel 6
Nilai Autocorrelation (AC) dan Partial Autocorrelation (PAC) PDRB Bali Triwulanan, Tahun 2000 – 2012 (Setelah dideferensi 1)
|
Lag |
AC |
Std.Error |
PAC |
Std.Error |
Box-Ljung Statistic | ||
|
Value |
Df |
Sig.(b) | |||||
|
1 |
0,306 |
0,136 |
0,306 |
00,140 |
5,074 |
1 |
0,024 |
|
2 |
-0,306 |
0,135 |
-0,441 |
0,140 |
10,231 |
2 |
0,006 |
|
3 |
-0,363 |
0,133 |
-0,127 |
0,140 |
17,643 |
3 |
0,001 |
|
4 |
-0,067 |
0,132 |
-0,008 |
0,140 |
17,902 |
4 |
0,001 |
|
5 |
0,018 |
0,130 |
-0,185 |
0,140 |
17,921 |
5 |
0,003 |
|
6 |
0,032 |
0,129 |
0,003 |
0,140 |
17,981 |
6 |
0,006 |
|
7 |
0,291 |
0,128 |
0,344 |
0,140 |
23,180 |
7 |
0,002 |
|
8 |
0,299 |
0,126 |
0,083 |
0,140 |
28,801 |
8 |
0,000 |
|
9 |
0,010 |
0,125 |
0,064 |
0,140 |
28,807 |
9 |
0,001 |
|
10 |
-0,227 |
0,123 |
0,078 |
0,140 |
32,201 |
10 |
0,000 |
|
11 |
-0,030 |
0,122 |
0,215 |
0,140 |
32,263 |
11 |
0,001 |
|
12 |
0,135 |
0,120 |
0,060 |
0,140 |
33,532 |
12 |
0,001 |
|
13 |
-0,047 |
0,119 |
-0,138 |
0,140 |
33,686 |
13 |
0,001 |
|
14 |
-0,194 |
0,117 |
-0,153 |
0,140 |
36,439 |
14 |
0,001 |
|
15 |
0,007 |
0,115 |
-0,030 |
0,140 |
36,443 |
15 |
0,002 |
|
16 |
0,271 |
0,114 |
0,054 |
0,140 |
42,119 |
16 |
0,000 |
Identifikasi ARIMA
Identifikasi ARIMA untuk PDRB dapat dilakukan dengan melihat correlogram dan partial correlogram data PDRB yang stationer setelah diferensi pertama (D1PDRBt). Untuk mendeteksi apakah pola AR atau MA atau ARIMA digunakan Tabel 6. Hasil Nilai
Autocorrelation (AC) dan Partial Autocorrelation (PAC) PDRB Bali Triwulanan, Tahun 2000 – 2012 (Setelah dideferensi 1), disajikan pada Tabel 6.
Pola nilai AC dan PAC dari PDRB triwulanan Provinsi Bali setelah didiferensi satu disajikan pada Gambar 5.

Gambar 5.
Pola Nilai Autocorrelation (AC) dan Partial Autocorrelation (PAC) PDRB Bali Triwulanan, Tahun 2000 – 2012 (Setelah dideferensi 1)
Dengan memperhatikan Tabel 5 dan Gambar 5 serta kriteria pada Tabel 1, yang mana pola AC dan PAC yang menurun secara drastis setelah lag 1, maka identifikasi model Model ARIMA secara tentatif sebagai berikut.
-
1) Model ARIMA (1,1,0) dengan persamaan:
D1PDRBt = β0+ β1AR(1) + et (18)
-
2) Model ARIMA (0,1,1) dengan persamaan:
D1PDRBt = β0 + β1MA(1) + et (19)
-
3) Model ARIMA (1,1,1) dengan persamaan:
D1PDRBt = β0+ β1AR(1) + β2MA(1) + et (20)
-
4) Model ARIMA (2,1,0) dengan persamaan:
D1PDRBt = β0+ β1AR(1) + β2AR(2) + et (21)
Berdasarkan empat model tentatif di atas berdasarkan Lampiran dapat diketahui estimasi koefisiennya seperti disajikan pada Tabel 7
Pada Tabel 7 terlihat bahwa pada model ARIMA(1,1,0) terlihat bahwa variable AR(1) berpengaruh nyata pada tingkaT signifikan 0,031, demikian juga konstannya pada tingkat 0,004. Pada
Model ARIMA(0,1,1) variabel MA(1) dan konstanta berpengaruh nyata pada signifikan kurang dari satu persen. Namun pada model ARIMA (1,1,1) variabel AR(1) dan MA(1) tidak berpengaruh nyata pada tingkat signifikan 5 persen. Pada model ARIMA (2,1,0) variabel AR(1), AR(2) dan konstantanya berpengaruh nyata pada signifikan kurang dari satu persen. Dengan melihat tingkat signifikansi masing-masing variabel terhadap model yang dibuat untuk sementara disimpulkan bahwa model ARIMA(2,1,0) adalah terbaik, sehingga tidak dibuat model lainnya.
Untuk meyakinkan model terbaik, maka dilakukan pemeriksaan terhadap nilai Akaike Information Criterion (AIC) yang dikembangkan oleh Prof. Harotugu Akaike, dan juga Bayesian Information Criteria (BIC) yang dikembangkan oleh Schwarz. Oleh karena dikembangkan oleh Schwarz, maka model BIC juga disebut model SIC. Dalam analisis ini semakin kecil nilai AIC, BIC atau SIC semakin baik model yang dibuat. Nilai AIC dan BIC dari model tentatif disajikan pada Tabel 8
Tabel 7
Estimasi PDRB Triwulanan Provinsi Bali dengan Model ARIMA (1,1,0), ARIMA (0,1,1), ARIMA(1,1,1), dan ARIMA(2,1,0)
|
Model/Paramater |
Variabel |
Estimates |
Std Error |
T |
Sig |
|
1) Model ARIMA(1,1,0) |
AR(1) | ||||
|
Non-Seasonal Lags |
0,301 |
0,14 |
2,216 |
0,031 | |
|
Constant |
84180,511 |
27627,38 |
3,047 |
0,004 | |
|
2) Model ARIMA (0,1,1) |
MA(1) | ||||
|
Non-Seasonal Lags |
-0,469 |
0,13 |
-3,691 |
0,001 | |
|
Constant |
84022,750 |
27126,77 |
3,097 |
0,003 | |
|
3) Model ARIMA (1,1,1) |
AR(1) MA(1) | ||||
|
Non-Seasonal Lags |
-0,061 |
0,31 |
-0,198 |
0,844 | |
|
-0,513 |
0,27 |
-1,905 |
0,063 | ||
|
Constant |
84067,295 |
26600,07 |
3,160 |
0,003 | |
|
4) Model ARIMA (2,1,0) |
AR1 | ||||
|
Non-Seasonal Lags |
AR2 |
0,434 |
0,129 |
3,368 |
0,002 |
|
-0,430 |
0,130 |
-3,319 |
0,002 | ||
|
Constant |
82448,642 |
17840,915 |
4,621 |
0,000 |
Sumber: Data Penelitian diolah
Tabel 8
Nilai AIC dan BIC Model ARIMA (1,1,0), (0,1,1), (1,1,1) dan (2,1,0)
|
Model |
AIC |
BIC |
|
ARIMA (1,1,0) |
1354,72 |
1358,58 |
|
ARIMA (0,1,1) |
1350,15 |
1354,01 |
|
ARIMA (1,1,1) |
1352,15 |
1357,94 |
|
ARIMA (2,1,0) |
1346,01 |
1351,81 |
Sumber: Data Penelitian diolah
Berdasarkan Tabel 8 dapat diketahui bahwa nilai AIC dan BIC yang minimum adalah model ARIMA( 2,1,0). Oleh karena itu model tersebut adalah model terbaik dari empat model yang dianalisis. Namun untuk lebih meyakinkan, maka model tersebut dilakukan uji diagnostik.
Uji Diagnostik Model ARIMA
Langkah berikutnya dari model ARIMA adalah melakukan uji diagnostic dari model ARIMA, yaitu dengan mendeteksi Nilai Autocorrelation (AC) dan Partial Autocorrelation (PAC) dan pengujian Box-Ljung Statistic dari residual model yang dipilih, dalam hal ini adalah ARIMA (2,1,0). Berdasarkan hasil ACF dan PACF dari nilai residual, seperti yang ditampilkan pada Tabel 9, ternyata pada Ljung-Box LB statistic
tidak ada yang signifikan. Hal ini dapat berarti bahwa nilai residual yang diestimasi adalah random (acak), sehingga dapat disimpulkan bahwa model ARIMA (2,1,0) adalah model terbaik.
Penelitian ini sesuai dengan yang dilakukan oleh Eka Ferri Indayani (2009) dengan penelitiannya yang berjudul Peramalan Jumlah Penumpang Kereta Api Dengan Menggunakan Metode Box-Jenkins (Studi Kasus di PT. Kereta Api (Persero) DAOP VI Yogyakarta) Dalam penelitian ini didapatkan model peramalan total jumlah penumpang kereta api khususnya untuk kelas bisnis, diperoleh ramalan total jumlah penumpang kereta api Yogyakarta adalah model ARIMA (1,0,1).
Penelitian ini juga memiliki kemiripan dengan yang dilakukan oleh Mei Taripar Pardamean pada tahun 2010, melakukan penelitian Analisa Box Jenkins Pada Pembentukan Model Produksi Premi Asuransi Kendaraan Bermotor Roda Empat di Jakarta. Temuannya adalah dengan menggunakan metode Box-Jenkins, produksi premi gabungan dan kerugian total mengandung unsur moving average dan membentuk model ARIMA (0,1,4) dan ARIMA (0,1,3). Namun produksi premi pihak ketiga mengandung unsur Autoregressive dan membentuk model ARIMA (3,0,0).
Penelitian menggunakan Box-Jenkins atau ARIMA juga didukung oleh penelitian yang dilakukan
|
Aulia Khair pada tahun 2011 mengenai Peramalan Average Precentage Error (MAPE) yang lebih baik. Beban Listrik Jangka Pendek Menggunakan Kombinasi Terbukti dari MAPE yang diperoleh selama 141 Dengan Autoregresive Integreted Moving Average peramalan pada tahun 2010, 5,16 persen untuk (ARIMA) dengan Regresi Linier Antara Suhu dan peramalan dengan menggunakan ARIMA, 5,28 persen Daya Listrik. Metode peramalan kombinasi antara untuk regresi linier, dan 4,19 persen untuk peramalan ARIMA dengan regresi linier memberikan Mean kombinasi antara ARIMA dengan regresi linier. | ||||||
|
Tabel 9 Nilai Autocorrelation (AC) dan Partial Autocorrelation (PAC) Residual Model ARIMA(2,1,0) PDRB Provinsi Bali | ||||||
|
Lag |
AC |
Std.Error PAC |
Std.Error |
Box-Ljung Statistic | ||
|
Value |
Df |
Sig.(b) | ||||
|
1 |
-0,050 |
0,136 -0,050 |
00,140 |
0,135 |
1 |
0,713 |
|
2 |
0,020 |
0,135 0,018 |
0,140 |
0,158 |
2 |
0,924 |
|
3 |
-0,182 |
0,133 -0,181 |
0,140 |
2,032 |
3 |
0,566 |
|
4 |
0,002 |
0,132 -0,017 |
0,140 |
2,032 |
4 |
0,730 |
|
5 |
0,022 |
0,130 0,028 |
0,140 |
2,061 |
5 |
0,841 |
|
6 |
-0,068 |
0,129 -0,102 |
0,140 |
2,338 |
6 |
0,886 |
|
7 |
0,274 |
0,128 0,276 |
0,140 |
6,960 |
7 |
0,433 |
|
8 |
0,189 |
0,126 0,247 |
0,140 |
9,203 |
8 |
0,325 |
|
9 |
0,106 |
0s,125 0,109 |
0,140 |
9,932 |
9 |
0,356 |
|
10 |
-0,164 |
0,123 -0,058 |
0,140 |
11,695 |
10 |
0,306 |
|
11 |
-0,005 |
0,122 0,063 |
0,140 |
11,697 |
11 |
0,387 |
|
12 |
0,069 |
0,120 0,100 |
0,140 |
12,028 |
12 |
0,443 |
|
13 |
-0,050 |
0,119 -0,072 |
0,140 |
12,203 |
13 |
0,511 |
|
14 |
-0,090 |
0,117 -0,180 |
0,140 |
12,800 |
14 |
0,542 |
|
15 |
-0,028 |
0,115 -0,152 |
0,140 |
12,860 |
15 |
0,613 |
|
16 |
0,246 |
0,114 0,115 |
0,140 |
17,532 |
16 |
0,352 |
|
Sumber: Data Penelitian diolah | ||||||
Peramalan PDRB Triwulanan Provinsi Bali dengan ARIMA (Box-Jenkins)
Berdasarkan Tabel 7 dapat dibuat model ramalan PDRB triwulanan Provinsi Bali:
ΔY’t = 82448,642 + 0,434 ΔYt-1 –0,430ΔYt-2 ………(22)
Dimana ΔY adalah perubahan dari PDRB. Untuk memperoleh proyeksi dari PDRB maka perubahan PDRB pada tahun ke-t ditambahkan dengan PDRB tahun sebelumnya. Dengan persamaan 4.12 program SPSS dapat diperintahkan untuk memproyeksi atau ramalan PDRB triwulanan Provinsi Bali dari triwulan I tahun 2013 sampai dengan triwulan 4 tahun 2014 dengan ramalan pisimis, moderat, dan optimis. Ramalan pisimis dan optimis diperoleh dari batas bawah dan batas atas pada derajat kepercayaan 95 persen, sedangkan ramalan moderat adalah rata-ratanya, seperti yang disajikan pada Tabel 10.
Tabel 10
Proyeksi PDRB Triwulanan Provinsi Bali dengan Model ARIMA (2,1,0) dengan Skenario Pisimis, Moderat, dan Optimis ( juta rupiah)
|
Ttriwulan |
Pisimis |
Moderat |
Optimis |
|
2013;1 |
8.261.212 |
8.516.837 |
8.772.461 |
|
2013;2 |
8.112.477 |
8.563.412 |
9.014.348 |
|
2013;3 |
8.090.357 |
8.641.319 |
9.192.280 |
|
2013;4 |
8.133.216 |
8.737.232 |
9.341.247 |
|
2014;1 |
8.175.308 |
8.827.476 |
9.479.643 |
|
2014;2 |
8.197.911 |
8.907.513 |
9.617.115 |
|
2014;3 |
8.215.331 |
8.985.561 |
9.755.791 |
|
2014;4 |
8.241.240 |
9.067.139 |
9.893.037 |
Sumber: Data Penelitian diolah
Berdasarkan Tabel 10 dapat diketahui bahwa PDRB Provinsi Bali dengan ramalan moderat pada triwulan I tahun 2013 sebesar Rp 8.516.837 juta, dan triwulan IV tahun 2014 adalah Rp 9.067.139 juta.
SIMPULAN DAN SARAN
Simpulan
Analisis data PDRB Provinsi Bali dari triwulan I tahun 2000 sampai dengan triwulan IV tahun 2012 dengan model Box-Jenkins diketahui bahwa model terbaik adalah dengan Autoregresif Integreted Moving Average atau ARIMA(2,1,0).
Perkiraan PDRB Provinsi Bali triwulan I tahun 2013 dengan ramalan moderat pada triwulan I tahun 2013 sebesar Rp 8.516.837 juta, dan triwulan IV tahun 2014 adalah Rp 9.067.139 juta.
Saran
Peneliti selanjutnya yang ingin membuat peramalan tentang PDRB sebaiknya mencari model peramalan selain ARIMA. Karena penggunaan peramalan dengan menggunakan ARIMA ini memiliki kelemahan dibandingkan dengan model peramalan yang berbasis teknologi informasi, misalnya MODFI dan yang lainnya.
REFERENSI
Abel, Andrew B. and Ben S. Bernake. 2001.
Macroeconomics. New York: Addison Wesley Longman, Inc.
Bank Indonesia Denpasar, 2013. Kajian Ekonomi Regional (KER) Provinsi Bali Triwulan IV-2012. Denpasar: Divisi Ekonomi Moneter -Kantor Perwakilan Bank Indonesia Denpasar.
BPS Provinsi Bali. 2013. Produk Domestik Regional
Bruto Provinsi Bali, Tahun 2008 – 2012.
Enders, 2008. Applied Econometrics Time Series: Second Edition. Wiley India: Pvt. Limited.
Ghozali, Imam. 2007. Aplikasi Analisis Multivariate dengan Program SPSS. Semarang: Badan Penerbit Universitas Diponegoro.
Gregory Paul. R and Robert C Stuart. 1992. Comparative Economic ‘System. Fourth Edition. New Jersey: Houghton Meffin Company.
Indayani, E.,F.2009. Peramalan Jumlah Penumpang Kereta Api Dengan Menggunakan Metode Box-Jenkins (Studi Kasus di PT. Kereta Api (Persero) DAOP VI Yogyakarta). E-journal. UIN Sunan Kalijaga Yogyakarta.
Khair, Aulia. 2011. Peramalan Beban Listrik Jangka Pendek Menggunakan Kombinasi Dengan Autoregresive Integreted Moving Average (ARIMA) dengan Regresi Linier Antara Suhu dan Daya Listrik. E-jurnal.Universitas Indonesia.
Pardamean, M.,T,. 2010. Analisa Box Jenkins Pada Pembentukan Model Produksi Premi Asuransi Kendaraan Bermotor Roda Empat. Jakarta: Ejournal. Universitas Guna Dharma.
Rahardja, Pratama dan Mandala Manurung, 2001. Teori Ekonomi Makro: Suatu Pengantar. Jakarta: LP FE Universitas Indonesia.
Widarjono, Agus. 2013. Ekonometrika: Pengantar dan Aplikasinya Disertai Panduan Eviews. Yogyakarta: UPP STIM YKPM.
Discussion and feedback